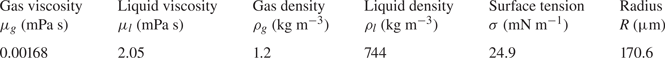1. Introduction
Droplet collisions have been extensively studied in past decades (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang, Umemura & Law Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997; Estrade et al. Reference Estrade, Carentz, Lavergne and Biscos1999; Brenn, Valkovska, & Danov Reference Brenn, Valkoyska and Danov2001; Pan, Law & Zhou Reference Pan, Law and Zhou2008; Pan, Chou & Tseng Reference Pan, Chou and Tseng2009; Zhang & Law Reference Zhang and Law2011; Tang, Zhang, & Law Reference Tang, Zhang and Law2012; Kwakkel, Breugem, & Boersma Reference Kwakkel, Breugem and Boersma2013; Huang & Pan Reference Huang and Pan2015; Li Reference Li2016; Pan et al. Reference Pan, Tseng, Chen, Huang, Wang and Lai2016, Reference Pan, Huang, Hsieh and Lu2019; Sommerfeld & Kuschel Reference Sommerfeld and Kuschel2016; Hu et al. Reference Hu, Xia, Li and Wu2017; Al-Dirawi & Bayly Reference Al-Dirawi and Bayly2019; Huang, Pan & Josserand Reference Huang, Pan and Josserand2019; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020) due to significant relevance to a variety of systems in natural and technological situations. Examples are seen in raindrop formation (Gunn Reference Gunn1965; Strangeways Reference Strangeways2006), medical therapy (May Reference May1973; Feng et al. Reference Feng, Kleinstreuer, Castro and Rostami2016), disease transmission (Tellier Reference Tellier2009; Gralton et al. Reference Gralton, Tovey, McLaws and Rawlinson2011) and combustion processes in engines (Chiu Reference Chiu2000; Zhang et al. Reference Zhang, Zhang, Yuan and Zhang2016). Typically, the collision outcomes of two identical droplets can be mapped in the regime diagrams depicted by a Weber number 
$(We = {\rho _l}{U^2}D/\sigma )$ and an impact parameter (B = χ/D = sin θ). They show coalescence after minor deformation (I), bouncing (II), coalescence after substantial deformation (III), reflexive separation (IV), stretching separation (V) (Ashgriz & Poo Reference Ashgriz and Poo1990; Qian & Law Reference Qian and Law1997) and rotational separation (VI) (Pan et al. Reference Pan, Huang, Hsieh and Lu2019). Here We indicates the ratio of impact inertia and surface tension force and B represents the effect of the colliding angle (θ) between the droplets. The inset of figure 1(a) shows a schematic for definitions of the collision parameters, where D denotes the droplet diameter, 
${\rho _l}$ and σ the density and surface tension of liquid, respectively, and χ the projection of the separation distance between the droplet centres in the direction normal to the relative velocity U.
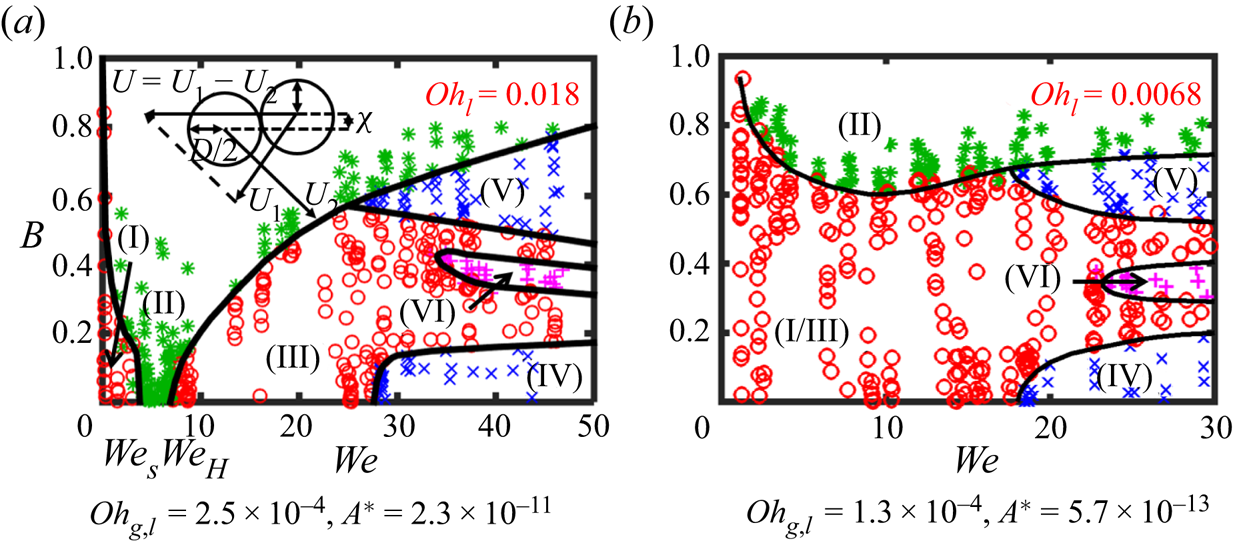
Figure 1. The regime diagrams in terms of the present experimental results of (a) dodecane and (b) water drops with a diameter 300 μm, showing a fully developed and partially developed bouncing regime, respectively. The symbols for indicating the regimes are: red circle, coalescence; blue cross, stretching/reflexive separation; green asterisk, bouncing; pink plus, rotational separation.
A typical regime diagram of alkane drops is shown in figure 1(a), featuring a fully developed bouncing regime (FB) where bouncing extends to B = 0. That is, non-monotonic transitions of regime (I)–(II)–(III) can be found by increasing We from O(0.1) to O(10) in both head-on and off-centre collisions. Here 
$W{e_S}$ and 
$W{e_H}$ denote the transition boundaries from regime (I) to (II) and from (II) to (III) at B = 0, respectively, for soft and hard collisions (Pan et al. Reference Pan, Law and Zhou2008). Compared with alkane drops, bouncing is not observed for head-on collisions (named partially developed bouncing regime, PB) of drops with high surface tension, such as water, as shown in figure 1(b). Such a distinction in the patterns of water and hydrocarbons was not realized until the discovery of the effect of the ambient gas pressure (Qian & Law Reference Qian and Law1997). Specifically, it was reported that increasing the gas density by raising the pressure or molecular weight of the ambient gas promotes bouncing and widens regime (II), while the opposite holds when reducing the density. As such, compared to atmospheric conditions, the bouncing regime is eliminated for alkane droplets on steadily decreasing the ambient pressure to 0.6 atm and it emerges for water droplets as the pressure is increased to 2.7 atm (Qian & Law Reference Qian and Law1997). Consequently, the key role of the inter-droplet gaseous film is revealed, whose development determines whether the impinging drops will rebound or merge. However, the influences of liquid properties on bouncing and coalescence regimes are not explicitly elucidated.
In addition to the surrounding gas properties, variation of the gas dynamics in the intervening gap and subsequently the propensity for bouncing are also found by adding surfactant into aqueous drops (Pan et al. Reference Pan, Tseng, Chen, Huang, Wang and Lai2016) and changing the liquid viscosity 
$({\mu _l})$ (Sommerfeld & Kuschel Reference Sommerfeld and Kuschel2016; Hu et al. Reference Hu, Xia, Li and Wu2017; Al-Dirawi & Bayly Reference Al-Dirawi and Bayly2019). Moreover, increasing the droplet diameter was found preliminarily in our prior experiment (Huang & Pan Reference Huang and Pan2015) and a numerical simulation (Li Reference Li2016) to enlarge the range between 
$W{e_S}$ and 
$W{e_H}$ for alkane drops. Li (Reference Li2016) indicated that the drop size effect on the bouncing phenomenon can be attributed to the competition between the capillary number 
$(C{a_g} = {\mu _g}U/\sigma = {\mu _g}We/\sqrt {{\rho _l}D\sigma } )$ and dimensionless mean free path 
$(\bar{\lambda } = \lambda /D)$, while the influence of 
$\bar{\lambda }$ consequentially determines the occurrence of droplet bouncing. Here 
${\mu _g}$ is the gas viscosity and 
$\lambda $ is the mean free path of gas. Compared with the other transitions involving merely hydrodynamically dominating phenomena such as coalescence to various types of separations which can be described based on the conservation laws (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang et al. Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997) using macroscopic fluid parameters, theoretical models for prediction of bouncing are relatively scarce. This is mainly due to the sophisticated interplays of multiple factors dominating the collision process which spans a wide range of length scales, involving distinct mechanisms specifically regarding the continuum and rarefied gas dynamics as well as compressibility and intermolecular forces (Pan et al. Reference Pan, Law and Zhou2008). As a consequence, the underlying parameters and their effects on bouncing cannot be comprehended in an explicit way by phenomenological models that provide correlations of the key dimensionless groups.
While some insights were gained in a few theoretical analyses tackling the whole set of governing equations or models (Gopinath, Chen & Koch Reference Gopinath, Chen and Koch1997; Gopinath & Koch Reference Gopinath and Koch2002), the parametric influence on the regime diagrams is not available until substantial computations are conducted, even merely for head-on collisions. There are few phenomenological models developed to predict the transitions between bouncing and coalescence, based on the criterion of energy balance, stating that bouncing occurs if the initial kinetic energy does not exceed the surface energy required to produce the maximum deformation (Estrade et al. Reference Estrade, Carentz, Lavergne and Biscos1999; Hu et al. Reference Hu, Xia, Li and Wu2017; Al-Dirawi & Bayly Reference Al-Dirawi and Bayly2019). They predict WeH without describing WeS and the non-monotonic transitions of regimes (I)–(II)–(III), by which the effects of liquid viscosity (Hu et al. Reference Hu, Xia, Li and Wu2017; Al-Dirawi & Bayly Reference Al-Dirawi and Bayly2019) and surface deformation (Estrade et al. Reference Estrade, Carentz, Lavergne and Biscos1999; Hu et al. Reference Hu, Xia, Li and Wu2017; Al-Dirawi & Bayly Reference Al-Dirawi and Bayly2019) are considered. Notwithstanding, the roles of μg and van der Waals (vdW) attraction are ignored, which are believed to play critical roles in causing repulsive pressure in the gas film and dominating droplet merging, respectively (Pan et al. Reference Pan, Law and Zhou2008; Zhang & Law Reference Zhang and Law2011; Kwakkel et al. Reference Kwakkel, Breugem and Boersma2013; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020), and hence should be accounted for in the bouncing process.
These results reveal significant difficulty for predicting the transitions of bouncing and coalescence due to the inherent complexity underlying the non-monotonic transitions from regimes (I) to (III) and that We alone would not be the sole parameter to describe the criteria. In the present study, we provide the first experimental evidence that the droplet size alone can change the bouncing regime essentially and hence the pattern of the We–B diagram. Specifically, by increasing D sufficiently, bouncing is observed in head-on collisions of water drops and, conversely, by decreasing D this regime is eventually annihilated in the head-on impacts of hydrocarbon drops. Consequently, in a way similar to that of the variation of ambient pressure (Qian & Law Reference Qian and Law1997; Reitter et al. Reference Reitter, Liu, Breitenbach, Huang, Bothe, Brenn, Pan, Roisman and Tropea2017), the forms of regime diagrams are unified for different liquids. Table 1 summarizes the ranges of the present key parameters that were covered in previous experimental studies, where 
${A^\ast } = {A_H}/\sigma {D^2}$, 
$O{h_l} = {\mu _l}/\sqrt {{\rho _l}D\sigma } $ and 
$O{h_{g,l}} = {\mu _g}/\sqrt {{\rho _l}D\sigma } $ are the dimensionless Hamaker constant, Ohnesorge number of liquid and two-phase Ohnesorge number, respectively. Here 
$O{h_{g,l}}$ was shown by Li (Reference Li2016) to describe the droplet deformation. Table 1 shows that the range of 
${A^\ast }$ in our study spans two orders of magnitude (5.1 × 10−13–8.2 × 10−11), which is the largest range among the parameters. Furthermore, the range of the present 
$O{h_{g,l}}$ data is also the widest (7.0 × 10−5–3.6 × 10−4) compared with other studies.
Table 1. The ranges of the dimensionless parameters used in the present and previous studies.
These scenarios can be comprehended by our scaling analyses for estimating the characteristic minimum gas-film thickness 
$({h_{m,c}})$, which has not been derived in previous studies of droplet bouncing after impact (Jiang et al. Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997; Klaseboer, Manica & Chan Reference Klaseboer, Manica and Chan2014; de Ruiter et al. Reference de Ruiter, Lagraauw, van den Ende and Mugele2015). By considering viscous dissipation in the drops and using a different scaling of 
$\partial h/\partial t$ in the lubrication equation, we have derived the key dimensionless parameters and give a criterion for prediction of bouncing for a wide range of fluid properties.
2. Experimental set-up
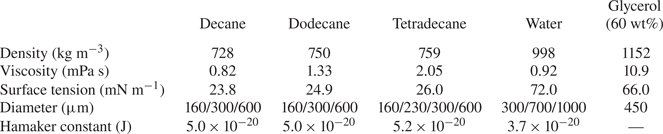
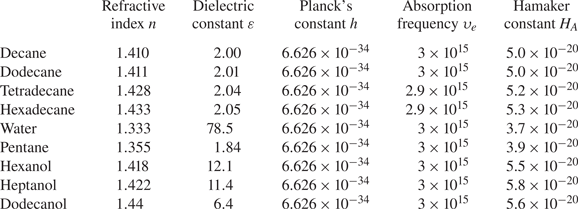
To set up the experiment, identical droplets of decane, dodecane, tetradcane or water were generated separately from two glass nozzles with fixed diameters by the conventional drop-on-demand method (Pan et al. Reference Pan, Chou and Tseng2009, Reference Pan, Tseng, Chen, Huang, Wang and Lai2016, Reference Pan, Huang, Hsieh and Lu2019; Huang & Pan Reference Huang and Pan2015; Huang et al. Reference Huang, Pan and Josserand2019). The properties of the tested liquids are listed in table 2, including a large range of surface tensions (23.8–72.0 mN m−1) and droplet diameters (160–1000 μm). In addition, the Hamaker constants of the liquids used in the present study are estimated by the Lifshitz theory (Lifshitz Reference Lifshitz1956; Israelachvili Reference Israelachvili2011). The relative velocity of colliding droplets can be controlled by the amplitude of periodic electric pulses and D can be finely adjusted (±1.6 %) by the electrical pulse width. We note that droplets with D = 1000 μm cannot be made due to the effect of gravity if the droplets are squeezed out horizontally from the nozzles, as demonstrated in previous experimental works (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang et al. Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997; Pan et al. Reference Pan, Law and Zhou2008, Reference Pan, Chou and Tseng2009, Reference Pan, Tseng, Chen, Huang, Wang and Lai2016, Reference Pan, Huang, Hsieh and Lu2019; Tang et al. Reference Tang, Zhang and Law2012; Huang & Pan Reference Huang and Pan2015; Sommerfeld & Kuschel Reference Sommerfeld and Kuschel2016; Huang et al. Reference Huang, Pan and Josserand2019). To overcome this restriction, we adopted another experimental set-up, as shown in figure 2, by squeezing out droplets vertically (Pan et al. Reference Pan, Chou and Tseng2009) such that droplets with D = 1000 μm can be made and the collisions were accomplished in the vertical plane. Via appropriate settings for the separation distance between the two nozzles and the delay time between two electrical pulses, droplets with a diameter of 1000 μm can be made sufficiently spherical and stable before each collision event. It is noted that since the Bond number (
$Bo = {\rho _l}g{D^2}/\sigma $, where g is the gravitational acceleration) of a 1.0 mm droplet is as small as 0.136 for water, the influence of gravity on droplet deformation can be neglected. The experimental images in figure 3 demonstrate ostensible sphericity for the droplets before impact.
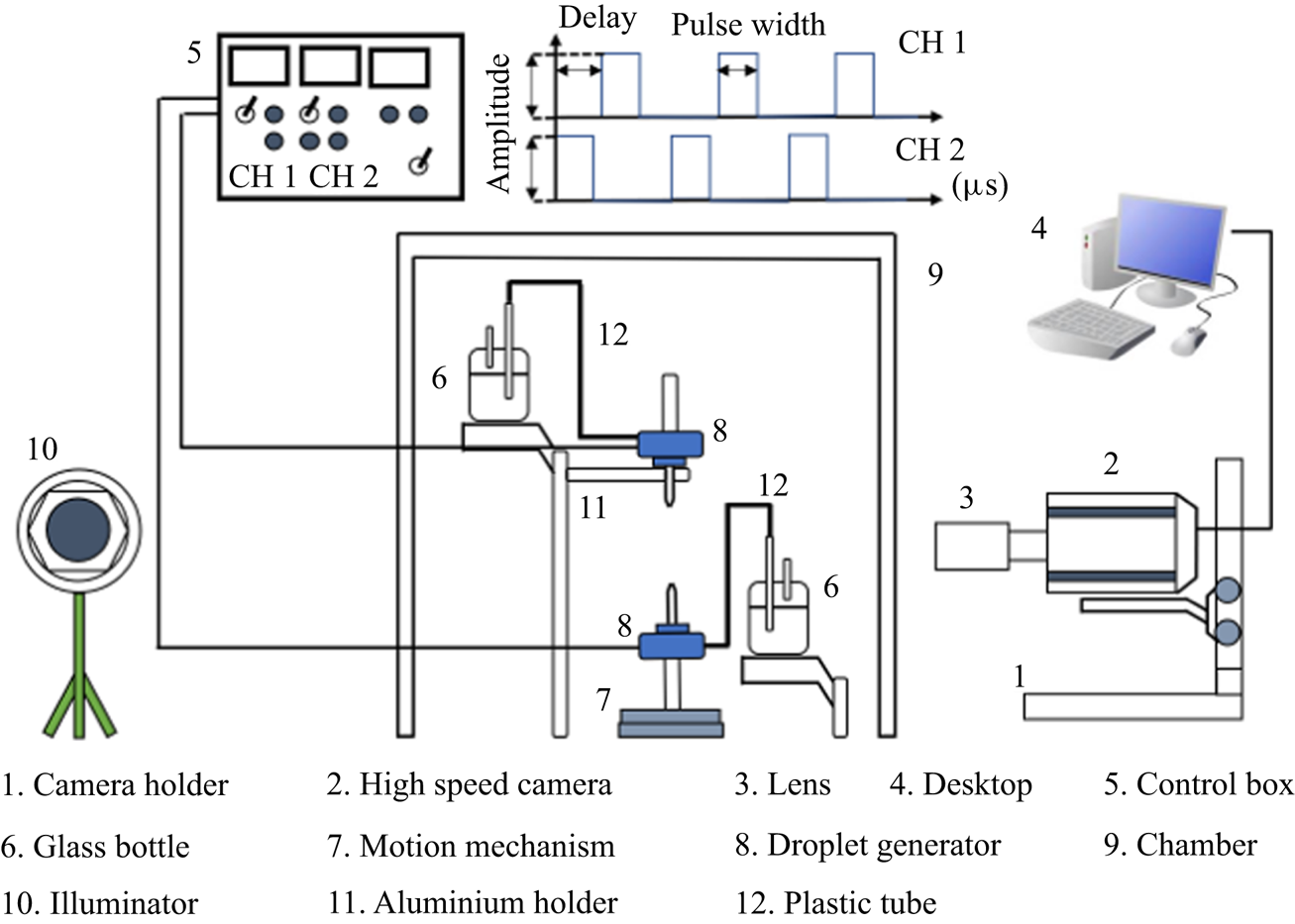
Figure 2. Experiment set-up for collisions of droplets with a diameter 1000 μm.
Figure 3. Collision sequences of dodecane drops with (a) D = 300 μm at We = 4.60, B = 0, (b) D = 160 μm at We = 4.70, B = 0, and of water drops with (c) D = 700 μm at We = 4.73, B = 0, (d) D = 1000 μm at We = 4.74, B = 0, (e) D = 700 μm at We = 4.68, B = 0.33 and (f) D = 1000 μm at We = 4.77, B = 0.32. Time unit: milliseconds.
Table 2. Properties of tested liquids (25 °C).
Time-resolved images were recorded by a high-speed CMOS digital camera (Vision Research, Phantom M310), which supported a resolution of 512 × 512 pixels up to 10 000 frames per second. A microscope lens (Navitar 6.5X) was mounted on the camera for increasing the spatial resolution up to 200 pixels mm−1. The exposure time of the shutter can be set down to 1 μs to avoid blurring due to background scattering. Surface tension of the tested liquids was measured by a tensiometer (DCAT, DataPhysics Instruments GmbH) with an accuracy of ±0.05 mN m−1 and the viscosity by a rheometer (Brookfield DV3 T, AMETEK Inc.) with an accuracy of 
${\pm} 0.01\;\; \textrm{mPa}\;\textrm{s}$. The uncertainties of We and B are ±3.7 % and ±1.6 %, respectively. In addition, the viscosity of air 
$({\mu _g})$ is taken to be 0.0186 mPa s. Our experiments were carried out at room temperature (25 °C) and at a relative humidity of 48 %. More experimental details are provided in Appendix A.
3. Results and discussion
3.1. Experimental results
Figure 3(a) shows the collision sequence of dodecane drops with diameters of 300 μm at We = 4.6, indicating that the colliding drops bounce away at t = 0.9 ms. Given almost the same We, however, the collision sequence with a smaller drop size (D = 160 μm) exhibits an entirely different outcome from that expected in figure 1(a). That is, the drops merge at t ~ 0.119 ms, as shown in figure 3(b). The same scenario resulting from the variation of droplet size is also found for water. Specifically, in contrast to coalescence of two water drops with D = 700 μm at We = 4.73 (figure 3c), they bounce away when D is increased to 1000 μm (figure 3d). Moreover, the droplet size effect on the bouncing regime can also be found in off-centre collisions. Figure 3(e) shows that at We = 4.68, water drops with D = 700 μm merge at t ~ 0.7 ms. However, at a similar value of We, when the diameter of the two water drops increases to 1000 μm, bouncing occurs after impact (figure 3f). This regime has never been observed in the literature for head-on collisions of water droplets (Ashgriz & Poo Reference Ashgriz and Poo1990; Tang, Zhang & Law Reference Tang, Zhang and Law2012; Huang & Pan Reference Huang and Pan2015; Li Reference Li2016; Pan et al. Reference Pan, Huang, Hsieh and Lu2019).
The regime diagrams with varying drop diameters of dodecane and water are shown in figure 4. Compared to the typical regime diagram of alkanes shown in figure 1(a), bouncing is absent in head-on collisions of dodecane drops with diameters of 160 μm (figure 4a). In contrast, when the droplet diameter is increased to 600 μm, the bouncing regime is dramatically enlarged and covers a substantial range of We at B = 0 (figure 4b). For water drops, the bouncing tendency is also promoted by increasing droplet diameter. As compared with figure 1(b), figure 4(c) shows that regime (II) occurs beyond B ~ 0.32 for the case of D = 700 μm while the minimum B is up to ~0.6 for D = 300 μm. Consequently, when the droplet diameter is further increased to 1000 μm, as shown in figure 4(d), a fully developed regime (II) can be observed, which is similar to the typical regime diagram of alkanes. The effect of varying D on regime (II) is also valid for other alkanes as shown in figure 5. With a droplet size as small as D = 160 μm for decane (figure 5a) and tetradecane (figure 5d), bouncing is not observed in head-on collisions, similar to the outcome for water drops usually reported (Ashgriz & Poo Reference Ashgriz and Poo1990; Qian & Law Reference Qian and Law1997; Estrade et al. Reference Estrade, Carentz, Lavergne and Biscos1999; Pan et al. Reference Pan, Law and Zhou2008). When the diameter is increased to 300 μm, the bouncing regime becomes fully developed, as shown in figures 5(b) and 5(e). By further increasing D to 600 μm (figure 5c,f), regime (II) is significantly expanded in the range We < 20 with a much larger 
$W{e_H}$ than that of D = 300 μm. These results clearly demonstrate that bouncing can be suppressed by decreasing the droplet diameter but encouraged by increasing it. This fact shows an analogous effect to changing the pressure of ambient gas (Qian & Law Reference Qian and Law1997; Reitter et al. Reference Reitter, Liu, Breitenbach, Huang, Bothe, Brenn, Pan, Roisman and Tropea2017), which could, however, be executed with much less effort, providing an appealing solution to manipulating bouncing readily.
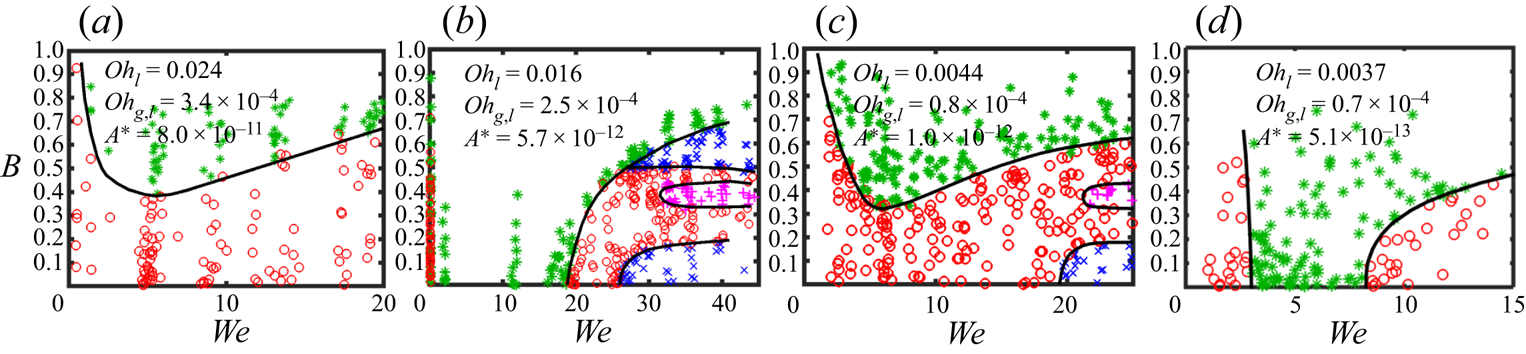
Figure 4. Regime diagrams for dodecane drops with diameters of (a) 160 and (b) 600 μm, and for water drops with diameters of (c) 700 and (d) 1000 μm.
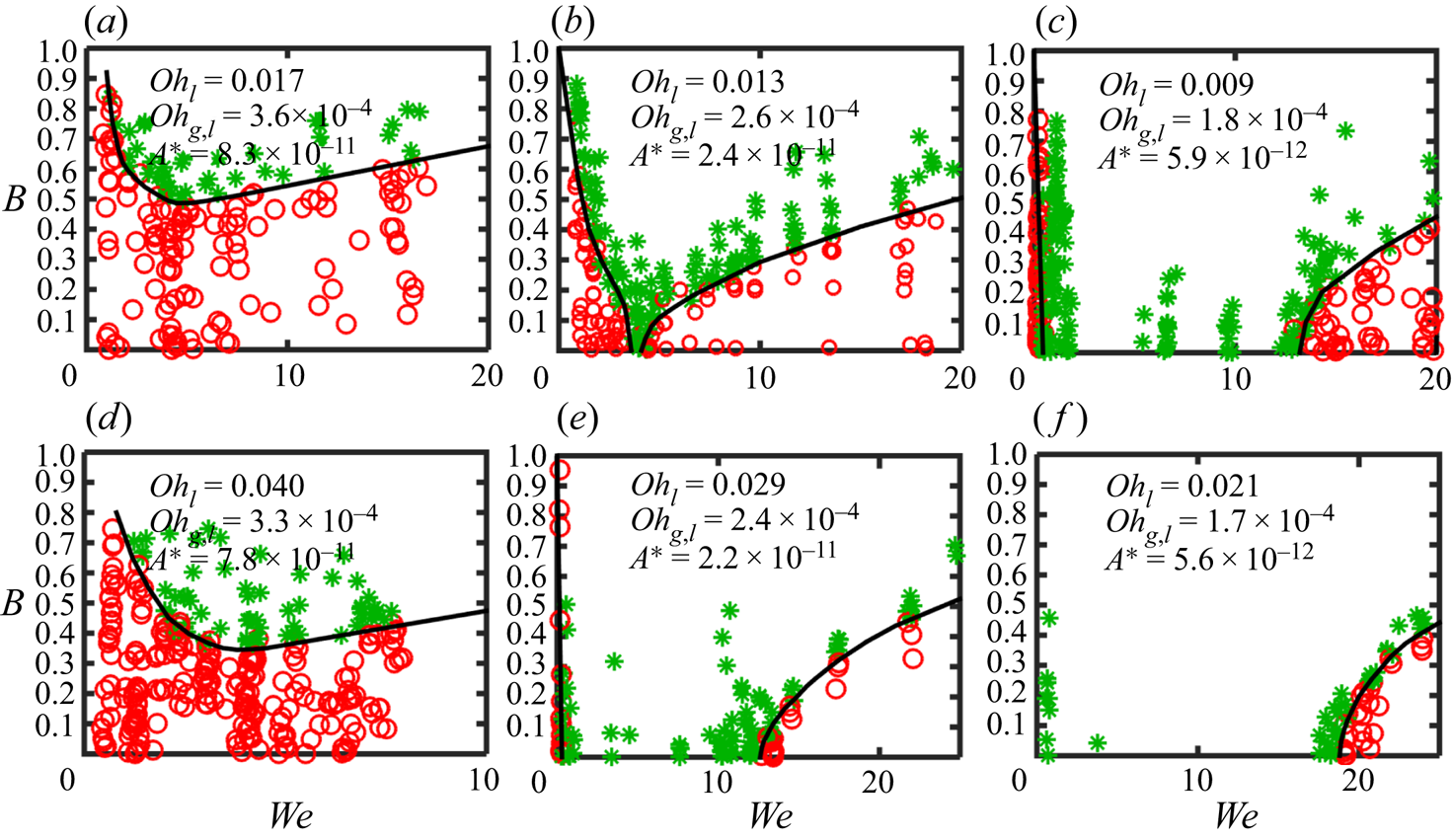
Figure 5. Regime diagrams for decane drops with (a) D = 160 μm, (b) 300 μm and (c) 600 μm; for tetradecane drops with (d) D = 160 μm, (e) 300 μm and (f) 600 μm.
3.2. Scaling analysis
3.2.1. Governing factors
To find the key dimensionless groups governing the development of bouncing in the regime diagrams, we consider the dynamics of the gas film formed between two approaching drops in head-on collisions. Previous studies have shown that coalescence occurs when the minimum thickness of the film 
$({h_m})$ is so small that vdW attraction can dominate the progress of approach (Pan et al. Reference Pan, Law and Zhou2008; Zhang & Law Reference Zhang and Law2011; Kwakkel et al. Reference Kwakkel, Breugem and Boersma2013; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020). In this regard, via the stress balance at the rim of the gas film at the stage when the interface is slightly deformed (figure 6b), we first estimate the characteristic minimum thickness of the gas film 
$({h_{m,c}})$ for each collision event. The scaling process is similar to that of a previous study that predicts the dimple height between an impinging drop and a solid surface (Klaseboer et al. Reference Klaseboer, Manica and Chan2014), whereas viscous dissipation is considered in the present impact of binary drops. The normal stress balance at the liquid–gas interface shows that
\begin{equation}{p_{g,r}} + \frac{\sigma }{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial h}}{{\partial r}}} \right) = {p_{l,r}}.\end{equation}
In (3.1), the pressure in the liquid at the rim, 
${p_{l,r}}$, is obtained from the simplified momentum equation (the derivation of which can be seen in Appendix C) along a streamline from the top to the rim of the drop, as shown in figure 6(b). As a consequence, 
${p_{l,r}}$ can be written as
\begin{equation}{p_{l,r}} \simeq
\frac{{2\sigma }}{R} + \frac{1}{2}{\rho
_l}{U^{\prime2}}.\end{equation}
Here 
$U^{\prime}$ is the velocity at the top of the drop, which can be obtained from the energy conservation, showing that
\begin{align}S{E_0} + \frac{1}{2}\left( {\frac{4}{3}{\rm \pi}{R^3}} \right){\rho _l}{U^2} = S{E_1} + \frac{1}{2}\left( {\frac{4}{3}{\rm \pi}{R^3}} \right){\rho _l}{U^{\prime2}} + {\mu _l}\int {\int_0^\tau {\frac{1}{2}{{\left[ {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right]}^2}\textrm{d}t\;\textrm{d}{x^3}} } .\end{align}
Here 
$S{E_0}$ is the surface energy before droplet impact and 
$S{E_1}$ is that at the stage with a small deformation. As justified by comparing the experimental images shown in figure 6, since the drop deformation is relatively small in the latter and the surface energy at the largest deformation (figure 3) is only about 16 % larger than the initial surface energy (Pan et al. Reference Pan, Law and Zhou2008), the difference between 
$S{E_0}$ and 
$S{E_1}$ can be neglected. By considering 
$\tau = R/U$ as the time scale, U the velocity scale and R the length scale, (3.3) becomes
\begin{equation}\frac{1}{2}{\rho _l}{U^{\prime2}} = \frac{1}{2}{\rho _l}{U^2} - \frac{{2{\mu _l}U}}{R}.\end{equation}
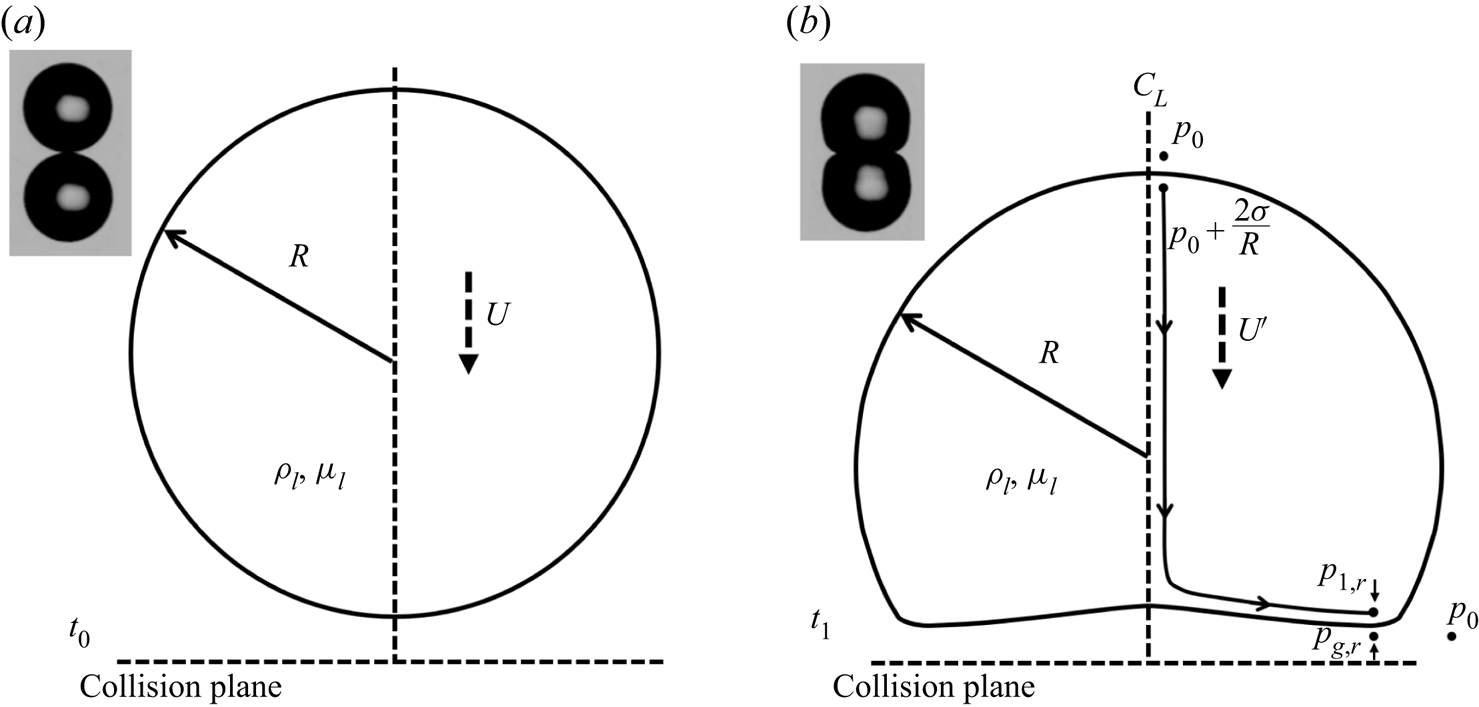
Figure 6. Schematic of a drop impacting a solid surface or another drop at the stage (a) before impact and (b) with a slight deformation.
The pressure in the gas film at the rim, 
${p_{g,r}}$, is estimated by the Stokes–Reynolds lubrication equation associated with the assumption of immobile liquid–gas interfaces, showing
\begin{equation}\frac{{\partial h}}{{\partial t}} = \frac{1}{{12{\mu _g}}}\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{h^3}\frac{{\partial {p_{g,r}}}}{{\partial r}}} \right).\end{equation}
The lubrication equation assumes that the characteristic length scale of the film thickness is significantly smaller than the film/drop radius, leading to negligibility of the inertial flow in the film. For the gas film between two approaching droplets, the film thickness is at least 100 times smaller than the droplet diameter (Pan et al. Reference Pan, Law and Zhou2008), satisfying this assumption. Moreover, previous numerical simulations based on the lubrication equation have shown good agreement with experimental images and indicated that the influence of gas density on droplet bouncing can be neglected (Zhang & Law Reference Zhang and Law2011; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020). Regarding the mobility of the liquid–gas interface, since the liquid viscosity is much higher than the air viscosity (Yiantsios & Davis Reference Yiantsios and Davis1990), and prior studies have experimentally suggested that the interfaces of drops or bubbles usually behave as tangentially immobile surfaces (Manica et al. Reference Manica, Parkinson, Ralston and Chan2010; Parkinson & Ralston Reference Parkinson and Ralston2010; Manica & Chan Reference Manica and Chan2011), we have assumed immobile liquid–gas interfaces. With t ~ R/U, 
$h\sim {h_{m,c}}$ and 
$r\sim \sqrt {R{h_{m,c}}} $, (3.5) becomes
\begin{equation}\frac{{{h_{m,c}}U}}{R} \simeq \frac{{{h_{m,c}}^2{p_{g,r}}}}{{12R{\mu _g}}},\end{equation}
and 
${p_{g,r}}$ can be shown as
\begin{equation}{p_{g,r}} \simeq \frac{{12{\mu _g}U}}{{{h_{m,c}}}}.\end{equation}By combining (3.1), (3.2), (3.4) and (3.7), the scaling relation is obtained as
\begin{equation}\frac{{12{\mu _g}U}}{{{h_{m,c}}}} \simeq \frac{\sigma }{R} + \frac{1}{2}{\rho _l}{U^2} - \frac{{2{\mu _l}U}}{R}.\end{equation}Thus (3.8) becomes
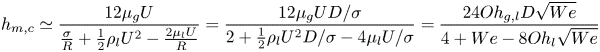\begin{align}{h_{m,c}} \simeq \frac{{12{\mu _g}U}}{{\frac{\sigma }{R} + \frac{1}{2}{\rho _l}{U^2} - \frac{{2{\mu _l}U}}{R}}} = \frac{{12{\mu _g}UD/\sigma }}{{2 + \frac{1}{2}{\rho _l}{U^2}D/\sigma - 4{\mu _l}U/\sigma }} = \frac{{24O{h_{g,l}}D\sqrt {We} }}{{4 + We - 8O{h_l}\sqrt {We} }}\end{align}and
\begin{equation}{H_{m,c}}(We) \simeq \frac{{24O{h_{g,l}}\sqrt {We} }}{{We + 4 - 8O{h_l}\sqrt {We} }},\end{equation}
where 
${H_{m,c}}$ is the dimensionless form of 
${h_{m,c}}$. Here 
$O{h_{g,l}} = {\mu _g}/\sqrt {{\rho _l}D\sigma } = C{a_g}W{e^{ - 0.5}}$, which is the newly derived two-phase Ohnesorge number.
In contrast to the present scaling analysis, Klaseboer et al. (Reference Klaseboer, Manica and Chan2014) ignored the coefficient 
$1/12$ in (3.5) and scaled the term 
$\partial h/\partial t$ as U, and the Laplace pressure as 
$\sigma /R$, leading to the result of 
${h_{m,c}} \simeq (D/2)\sqrt {2O{h_{g,l}}\sqrt {We} /(2 + We + 0.5Bo)} $. Here we have kept the coefficient 
$1/12$ and scaled 
$\partial h/\partial t$ as 
${h_{m,c}}/(R/U)$, and the Laplace pressure as 
$2\sigma /R$. This yields the results that our 
${h_{m,c}}$ values are about 3 times smaller than the dimple height predicted by Klaseboer et al. (Reference Klaseboer, Manica and Chan2014), which are closer to previous numerical results (Pan et al. Reference Pan, Law and Zhou2008). Moreover, with the scaling of Laplace pressure 
$2\sigma /R$, the transitional We from PB to FB is derived.
3.2.2. Universal phenomena in drop impacts
Figure 7(a) plots 
${h_{m,c}}$ as a function of We in (3.9) for different properties of drops, showing that 
${h_{m,c}}$ initially increases and then decreases as We increases. The non-monotonic trend of 
${h_{m,c}}$–We curves is similar to the variations of dimple height and the minimum thickness scaled in Pan (Reference Pan2004), Pan & Law (Reference Pan and Law2004) and Klaseboer et al. (Reference Klaseboer, Manica and Chan2014). Strikingly, without any empirical factor, the 
${h_{m,c}}$ values exhibit the same order of magnitude as a previous numerical prediction based on the continuum assumption (Pan et al. Reference Pan, Law and Zhou2008) but they are one order of magnitude larger than those of the simulations including rarefied gas effect (Zhang & Law Reference Zhang and Law2011; Kwakkel et al. Reference Kwakkel, Breugem and Boersma2013; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020). Furthermore, by taking the derivative 
$\textrm{d}{h_{m,c}}/\textrm{d}We = 0$, we can find the maximum 
${h_{m,c}}(We)$, 
${h^{\prime}_{m,c}} = 6O{h_{g,l}}D/(1 - 2O{h_l})$, at We = 4, which is denoted by 
$We^{\prime}$, for every set of drops with any given 
$O{h_{g,l}}$ and 
$O{h_l}$. To further identify the transitional We from PB to FB experimentally, we have obtained the regime diagrams of tetradecane drops with D = 230 μm and drops of a glycerol solution with D = 450 μm, as shown in the figure 8. It is observed that a small range of bouncing intervenes in head-on collisions (We = 2.0–4.5). Therefore, we can estimate the transitional We by the average of 
$W{e_S}$ and 
$W{e_H}$, i.e. We′ = 3.3. This is quite close to the universal value as derived.
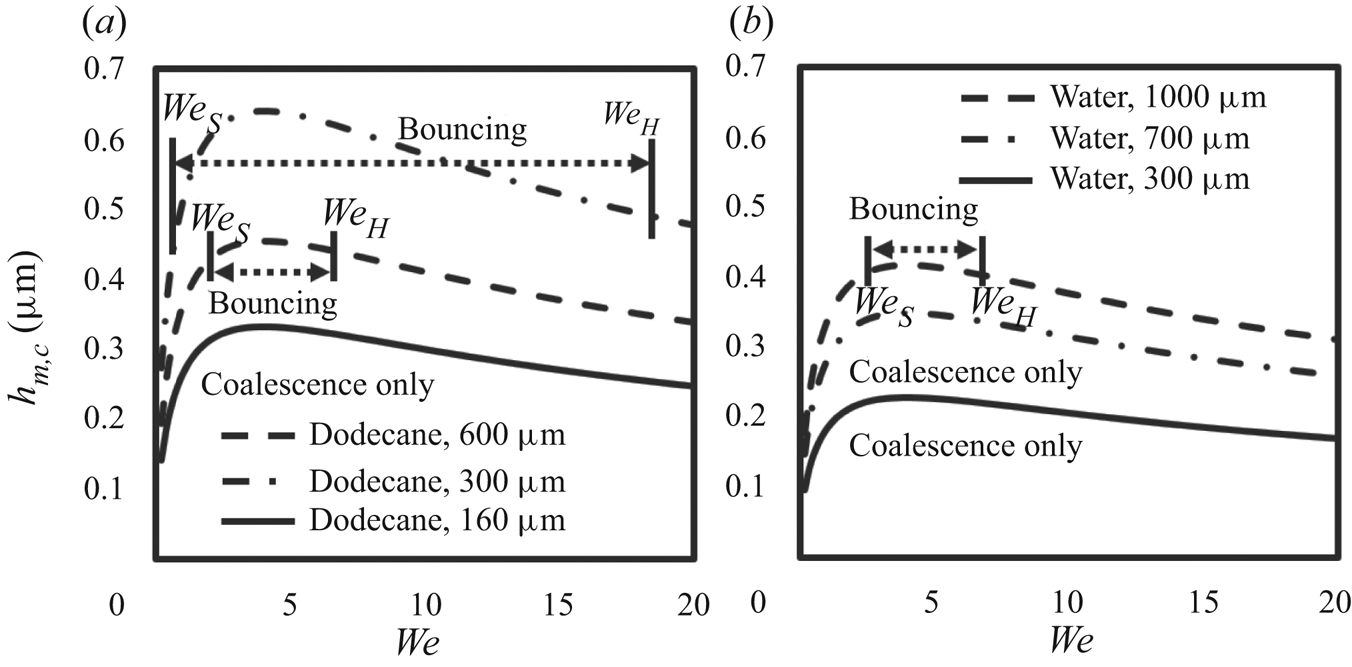
Figure 7. Characteristic minimum thickness of the gas film as a function of We in (3.9) for (a) dodecane and (b) water drops, where the experimentally obtained WeS and WeH are indicated.
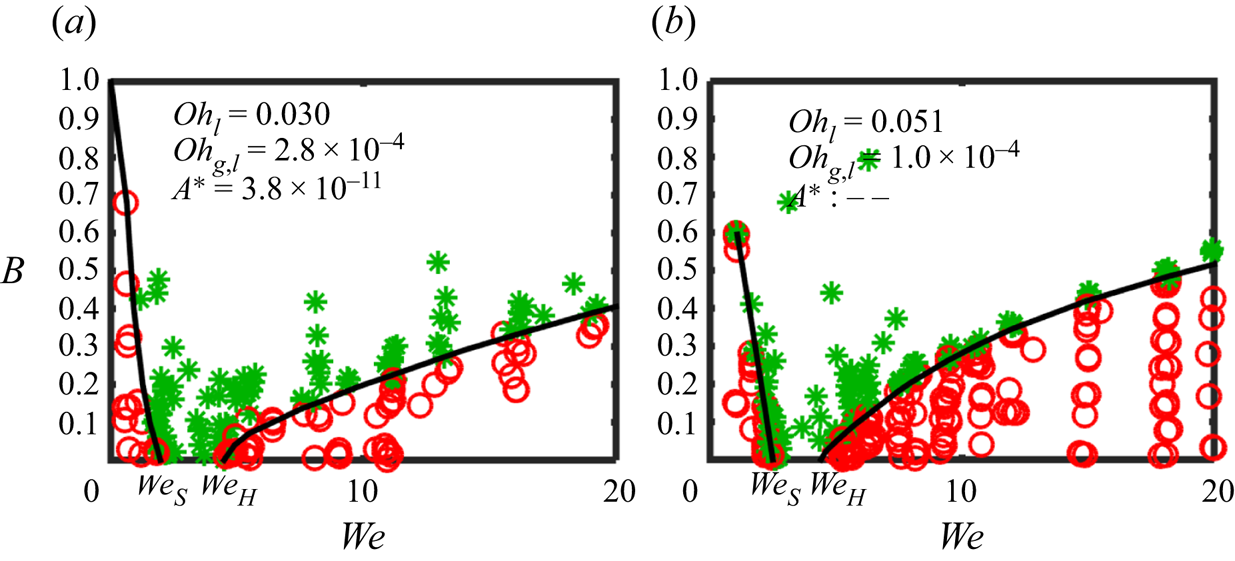
Figure 8. Regime diagram for (a) tetradecane drops with D = 230 μm and Ohl = 0.030 and (b) glycerol–water solution (60 %) drops with D = 450 μm and Ohl = 0.051.
Equation (3.9) shows that when 
$We \ll We^{\prime}$ (
${\textstyle{1 \over 2}}{\rho _l}{U^2} \ll \sigma /R$ and 
$2{\mu _l}U/R \ll \sigma /R$), 
${h_{m,c}}$ is dominated by the ratio between 
$12{\mu _g}U$ and 
$\sigma /R$, and thus increases with We 
$({h_{m,c}} \propto O{h_{g,l}}D\sqrt {We} )$. On the other hand, when 
$We \gg We^{\prime}$ (
${\textstyle{1 \over 2}}{\rho _l}{U^2} \gg \sigma /R$ and 
${\textstyle{1 \over 2}}{\rho _l}{U^2} \gg 2{\mu _l}U/R$), 
${h_{m,c}}$ is dominated by the ratio between 
$12{\mu _g}U$ and 
${\textstyle{1 \over 2}}{\rho _l}{U^2}$, and thus decreases as We increases 
$({h_{m,c}} \propto O{h_{g,l}}D/\sqrt {We} )$. The fidelity of 
$We^{\prime}$ can be verified by the regime diagram shown in figures 1(a) and 8, and the available data for drop–drop collisions (Jiang et al. Reference Jiang, Umemura and Law1992), demonstrating the transitional We from PB to FB being located in the range 3.3 to 4.5 with Ohl = 0.006–0.051. Moreover, 
$We^{\prime}$ is almost the same as the mid-value of the bouncing range for droplets impacting a solid surface (de Ruiter et al. Reference de Ruiter, Lagraauw, van den Ende and Mugele2015). This justifies the same nature of droplet bouncing in drop–drop and drop–surface impacts for which the exclusive value of 
$We^{\prime}$ gives a universal outcome of the transition.
3.2.3. Effects of droplet size and fluid properties
Equation (3.9) describes the exclusive influence of droplet size found in the experiments. For the series of dodecane drops with D = 300 and 600 μm, as shown in figure 7(a), 
$W{e_S}$ and 
$W{e_H}$ are located at the opposite sides of the corresponding maximum 
${h_{m,c}}$ within which bouncing occurs and 
${h_{m,c}}$ is larger than that outside where coalescence results. By decreasing D to 160 μm, the 
${h_{m,c}}$ values become the smallest compared with those for the other sizes of drops and no bouncing can be observed. The same evolution of We–
${h_{m,c}}$ curves with varying droplet size is also found for water drops as shown in figure 7(b). It is seen that at the smallest diameter (300 μm), the value of 
${h_{m,c}}$ is the smallest compared with that for the other droplet sizes. When D is increased to 1000 μm, the 
${h_{m,c}}$ curve is raised and a bouncing regime is formed around the maximum value.
The effects of fluid properties such as surface tension on bouncing can also be realized via (3.9). Considering drops with identical D (300 μm) but distinct surface tensions, bouncing occurs in cases of dodecane drops featuring a smaller surface tension and larger values of 
${h_{m,c}}$ (figure 7a). On the other hand, water drops having a larger surface tension have rendered smaller values of 
${h_{m,c}}$ (figure 7b), yielding only coalescence in head-on collisions. Surprisingly, comparing the cases showing similar magnitudes of 
${h_{m,c}}$, i.e. dodecane drops with D = 300 μm (figure 7a) and water drops with D = 1000 μm (figure 7b), the values of 
$W{e_S}$ and 
$W{e_H}$ and hence the bouncing range are quite similar. This reveals the applicability of 
${h_{m,c}}$ as an index for evaluation of bouncing in a head-on impact and hence the formation of a fully developed regime (II).
Figure 7 demonstrates a consistency between the trend predicted by (3.9) and the non-monotonic transitions of coalescence (I) to bouncing (II) and to coalescence (III) again in the regime diagrams depicted by the experimental results. This indicates that bouncing may occur when 
${h_{m,c}}$ is sufficiently large, i.e. beyond a certain threshold, and can explain the influence of various fluid properties found in previous studies. For instance, the effect of droplet size mentioned by Li (Reference Li2016) can be understood from figure 7, showing that a larger droplet diameter leads to a larger 
${h_{m,c}}$ and thus promotes occurrence of bouncing. This scaling prediction unambiguously interprets the experimental finding of the present study of the development of the bouncing regime with varying droplet diameter and fluid properties. Specifically, (3.9) shows that 
${h_{m,c}}$ increases as 
$O{h_l}$ or 
$O{h_{g,l}}$ increases, which can be achieved by increasing 
${\mu _l}$ or 
${\mu _g}$ as discussed in previous work (Jiang et al. Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997; Estrade et al. Reference Estrade, Carentz, Lavergne and Biscos1999; Zhang & Law Reference Zhang and Law2011; Tang et al. Reference Tang, Zhang and Law2012; Kwakkel et al. Reference Kwakkel, Breugem and Boersma2013; Huang & Pan Reference Huang and Pan2015; Li Reference Li2016; Pan et al. Reference Pan, Tseng, Chen, Huang, Wang and Lai2016; Sommerfeld & Kuschel Reference Sommerfeld and Kuschel2016; Hu et al. Reference Hu, Xia, Li and Wu2017; Al-Dirawi & Bayly Reference Al-Dirawi and Bayly2019), thus enhancing the propensity for droplet bouncing. On the contrary, a larger surface tension contributes to smaller 
$O{h_l}$ and 
$O{h_{g,l}}$, leading to a smaller 
${h_{m,c}}$ and thus to a higher tendency towards coalescence, as observed previously (Ashgriz & Poo Reference Ashgriz and Poo1990; Jiang et al. Reference Jiang, Umemura and Law1992; Qian & Law Reference Qian and Law1997; Estrade et al. Reference Estrade, Carentz, Lavergne and Biscos1999; Zhang & Law Reference Zhang and Law2011).
3.3. Critical film thickness and criterion of droplet merging
The results in figure 7 indicate a consensus with previous understanding that droplet merging occurs if the minimum film thickness is small enough to be dominated by vdW forces (Gopinath & Koch Reference Gopinath and Koch2002; Pan et al. Reference Pan, Law and Zhou2008; Zhang & Law Reference Zhang and Law2011; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020). To further assess the critical thickness, 
${h_{cr}}$, in a quantitative manner, we consider the condition when the disjoining pressure given by the vdW force which tends to destabilize the interfaces becomes comparable to the capillary pressure of surface tension that is opposing the fluctuations (Vaynblat, Lister & Witelski Reference Vaynblat, Lister and Witelski2001; Yoon et al. Reference Yoon, Baldessari, Ceniceros and Leal2007; Ardekani & Joseph Reference Ardekani and Joseph2009; Thete et al. Reference Thete, Anthony, Basaran and Doshi2015). From the scaling relation, 
${A_H}/6{\rm \pi} h_{cr}^3\sim 4\sigma /D$, we obtain 
${h_{cr}}$ and the dimensionless critical thickness:
\begin{equation}{H_{cr}} = \frac{{{h_{cr}}}}{D}\sim \sqrt[3]{{\frac{{{A_H}}}{{24{\rm \pi} \sigma {D^2}}}}} = \sqrt[3]{{\frac{{{A^\ast }}}{{24{\rm \pi} }}}},\end{equation}
where 
${A_H}$ is the Hamaker constant and 
${A^\ast } = {A_H}/\sigma {D^2}$ the dimensionless Hamaker constant (Erneux & Davis Reference Erneux and Davis1993; Yoon et al. Reference Yoon, Baldessari, Ceniceros and Leal2007; Ardekani & Joseph Reference Ardekani and Joseph2009). Critical thickness 
${h_{cr}}$ has long been studied (Ivanov et al. 1970; Ivanov Reference Ivanov1988; Yoon et al. Reference Yoon, Baldessari, Ceniceros and Leal2007; Ardekani & Joseph Reference Ardekani and Joseph2009; Kaur & Leal Reference Kaur and Leal2009) and found to depend mainly on the dimensionless Hamaker constant (Yoon et al. Reference Yoon, Baldessari, Ceniceros and Leal2007; Ardekani & Joseph Reference Ardekani and Joseph2009; Kaur & Leal Reference Kaur and Leal2009). Furthermore, in this scaling analysis, due to the neglecting of gas inertia in the lubrication equation as discussed, the effect of the Ohnesorge number of the gas film, i.e. 
$O{h_g} = {\mu _g}/\sqrt {{\rho _g}D\sigma } $, is not considered. Therefore, the dominance of A* on 
${h_{cr}}/D$ is justified as shown in (3.11). It is also noted that, while more complications could be rendered by varying B, here we consider only head-on collisions due to the significance in marking off the formation of a FB in binary droplet collisions.
In (3.11), the scaled values of 
${h_{cr}}$, which is independent of We, are of the same order of magnitude as that approximated in previous studies (Yoon et al. Reference Yoon, Baldessari, Ceniceros and Leal2007; Ardekani & Joseph Reference Ardekani and Joseph2009; Thete et al. Reference Thete, Anthony, Basaran and Doshi2015), showing that droplet merging occurs when the minimum thickness of the gas film falls in the range 100–1000 Å. This critical thickness suggests a threshold for determination of bouncing. Specifically, with reference to the non-monotonic trend shown by (3.9) in figure 7 and prior criterion of coalescence, if 
${h^{\prime}_{m,c}}$ is smaller than 
${h_{cr}}$, the values of 
${h_{m,c}}$ within the whole range of We are lower than that of 
${h_{cr}}$, and thus coalescence dominates all the way in head-on collisions. Conversely, when 
${h^{\prime}_{m,c}}$ is larger than 
${h_{cr}}$, bouncing can be created within some range of We in head-on collisions; thus a fully developed regime (II) is observable.
Based on these results, it is reasonable to propose a criterion specifying that, if 
${h^{\prime}_{m,c}}$ is larger than the critical film thickness, i.e. 
${h^{\prime}_{m,c}} > {C_1}{h_{cr}}$, where C 1 is an empirical coefficient, bouncing can be generated in head-on impacts and thus the corresponding regime is fully developed in the diagram. With reference to the present and previous experimental data (Jiang et al. Reference Jiang, Umemura and Law1992; Tang et al. Reference Tang, Zhang and Law2012; Sommerfeld & Kuschel Reference Sommerfeld and Kuschel2016), the occurrence of a fully developed bouncing regime for different fluid properties is found to follow this criterion with the fitting coefficient C 1 = 21.1. Figure 9(a) shows that the regime diagrams with FB (open symbols) are all located above 
${h^{\prime}_{m,c}} = 21.1{h_{cr}}$ (black solid line) and those exhibiting PB are below. Specifically, when surface tension decreases or the drop diameter increases, both 
${h^{\prime}_{m,c}}$ and 
${h_{cr}}$ increase, with the increase of 
${h_{cr}}$ being much less than that of 
${h^{\prime}_{m,c}}$. Consequently, when 
$h{^{\prime}_{m,c}} > 21.1{h_{cr}}$, i.e. 
$1.2O{h_{g,l}}/(1 - 2O{h_l}) > \sqrt[3]{{{A^\ast }}}$, the regime diagram transforms to that with FB, yielding bouncing in head-on collisions. In a more generic way, the present thickness-based criterion is manifested in a dimensionless form plotted in figure 9(b), where the effects of various fluid properties can be understood through the relation of 
${H^{\prime}_{m,c}}$ versus 
${H_{cr}}$. By increasing 
$O{h_{g,l}}$, e.g. by increasing gas viscosity or decreasing surface tension, a larger 
${H^{\prime}_{m,c}}$ results, thus encouraging droplet bouncing and FB. On the other hand, by decreasing D or increasing 
${A_H}$, a larger 
${H_{cr}}$ is yielded, thus encouraging coalescence and PB. In addition, the influence of liquid viscosity on droplet bouncing is revealed by 
${H^{\prime}_{m,c}} = 6{\mu _g}/(1 - 2O{h_l})\sqrt {{\rho _l}D\sigma } $, showing that increasing liquid viscosity increases 
${H^{\prime}_{m,c}}$ and hence enhances droplet bouncing. The parameters used in figure 9 can be seen in Appendix B.
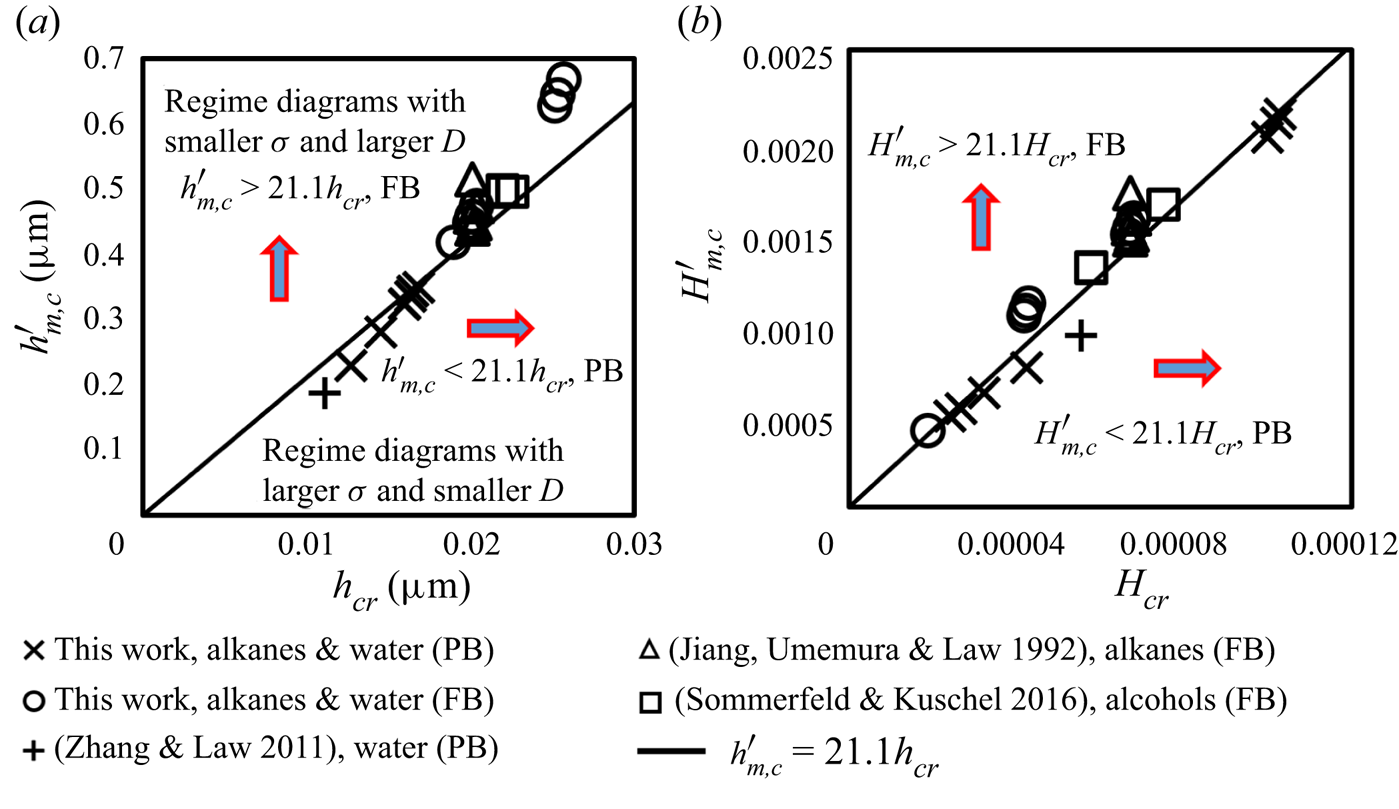
Figure 9. Graphs for predicting the occurrence of PB and FB at fixed dimensionless groups 
$(O{h_{g,l}},\;O{h_l},\;{A^\ast })$ with (a) dimensional thickness 
$({h^{\prime}_{m,c}},{h_{cr}})$ and (b) dimensionless thickness 
$({H^{\prime}_{m,c}},{H_{cr}})$. Here 
${H_{cr}} = {({A^\ast }/24{\rm \pi})^{1/3}}$ and 
${H^{\prime}_{m,c}} = 6O{h_{g,l}}{(1 - 2O{h_l})^{ - 1}}$.
The dimensionless parameters 
$(O{h_{g,l}},\;O{h_l},\;{A^\ast })$ used here are derived based on the physical principles that govern the hydrodynamics in colliding drops and intervening gas film, i.e. the momentum conservation in the liquid and gas phases and the stress balance on the liquid–gas interface (Pan et al. Reference Pan, Law and Zhou2008; Zhang & Law Reference Zhang and Law2011; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020), as well as the energy conservation in the liquid phase. By using these dimensionless parameters that can describe the bouncing/coalescent dynamics of two drops, the transition from PB to FB can be predicted not only for our experimental data, but also for other types of droplets such as alcohol, water and alkanes with different diameters (Jiang et al. Reference Jiang, Umemura and Law1992; Tang et al. Reference Tang, Zhang and Law2012; Huang & Pan Reference Huang and Pan2015; Sommerfeld & Kuschel Reference Sommerfeld and Kuschel2016). The model proposed in the present study is applicable to all the existing data (
$O{h_{g,l}} = 0.7 \times {10^{ - 4}}\text{--}3.6 \times {10^{ - 4}}$, Ohl = 0.003–0.282, 
${A^\ast } = 5.1 \times {10^{ - 13}}\text{--} 8.21 \times {10^{ - 11}}$), and it is reasonable to assume its validity for other droplet collision systems that are governed by the same physical laws.
4. Concluding remarks
We have experimentally demonstrated the unique effects of droplet size on bouncing phenomena in droplet collisions for alkanes, water and glycerol solutions having distinct properties. It is found that given a sufficiently large droplet diameter for water, the bouncing regime can extend from off-centre conditions to head-on impacts. Conversely, by decreasing the droplet size sufficiently, bouncing can be totally eliminated in head-on collisions of alkane drops. That is, bouncing is promoted by increasing droplet diameter but suppressed by decreasing it. By deriving the characteristic minimum thickness of the intervening gas film via a scaling analysis, we show that a larger 
${h_{m,c}}$ yields a greater tendency to produce bouncing. The scaled 
${h_{m,c}} \propto D$ is coincident with previous scaling results neglecting the effect of liquid viscosity, showing that the film thickness (h) increases as D increases (Mani, Mandre & Brenner Reference Mani, Mandre and Brenner2010; Duchemin & Josserand Reference Duchemin and Josserand2011; Klaseboer et al. Reference Klaseboer, Manica and Chan2014). Moreover, by comparing the non-monotonic function of 
${h_{m,c}}(We)$ and the threshold for droplet coalescence, 
${h_{cr}}$, a scaling relation is established to determine whether bouncing can occur in head-on collisions. Therefore, the occurrence of the non-monotonic coalescence–bouncing–coalescence transitions can be foreseen by simply using the dimensionless group 
$(O{h_{g,l}},\;O{h_l},\;{A^\ast })$ without resorting to full-field numerical simulations that may account for more detailed structures such as rarefied gas dynamics and compressibility. The inevitably included sole coefficient is fitted from a large pool of available data covering the present and previous experimental results, which would apply to a considerable range of 
$(O{h_{g,l}},\;O{h_l},\;{A^\ast })$.
The effect of gas rarefaction has been indicated in previous models, showing that 
${\mu _g}$ can be reduced by dividing a reduction factor, 
$\Delta (Kn)$, for h around the mean free path of gas (Pan et al. Reference Pan, Law and Zhou2008; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020). Here 
$Kn = \lambda /h$, which is the Knudsen number, and 
$\Delta (Kn) \ge 1$, increasing monotonically as 
$Kn$ increases. Li (Reference Li2016) stated that a larger D contributed to a smaller 
$\bar{\lambda }$, leading to a lesser reduction of 
${\mu _g}$ and droplet bouncing. However, the reduction of 
${\mu _g}$ is actually dominated by 
$Kn$ (Pan et al. Reference Pan, Law and Zhou2008; Li Reference Li2016; Chubynsky et al. Reference Chubynsky, Belousov, Lockerby and Sprittles2020), indicating that a larger h contributes to a smaller 
$Kn$ (
${\propto} 1/h$) and a lesser reduction of 
${\mu _g}$, thus promoting droplet bouncing. Surprisingly, based on the hydrodynamic scaling relations, the result of 
${h_{m,c}} \propto D$ demonstrates the influence of drop size on bouncing, which is further modified by a congruent effect of rarefied gas dynamics, showing that 
$Kn \propto 1/{h_{m,c}}$. Consequently, the parametric influences on bouncing can be elucidated in terms of the macroscopic parameters.
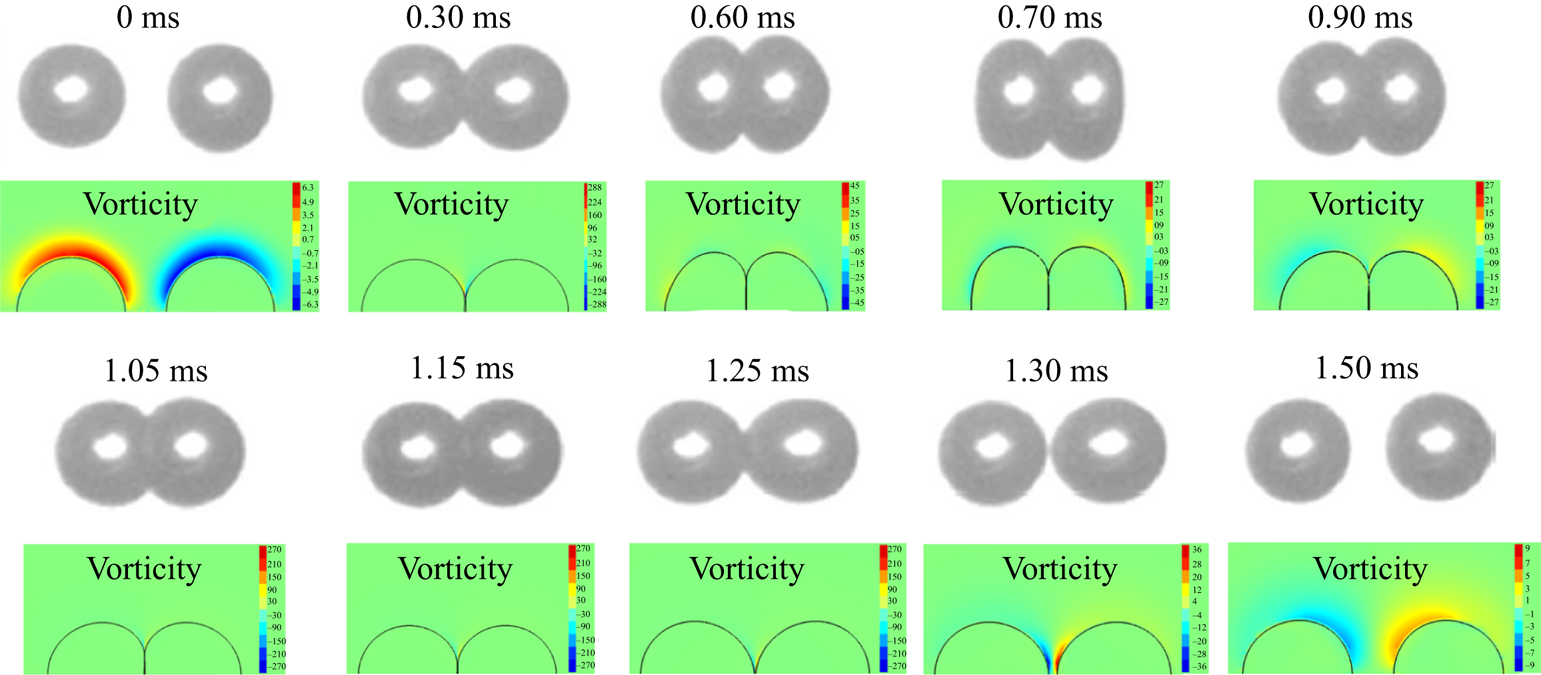
Figure 10. Comparison between the experimental images (Pan, Law & Zhou Reference Pan, Law and Zhou2008) and the numerical simulation for bouncing tetradecane droplets of equal size (D = 341.2 μm and U = 0.486 m s−1). The parameters used in the simulation are the same as the experimental conditions of Pan et al. (Reference Pan, Law and Zhou2008), where the colour bar indicates the magnitude of vorticity.
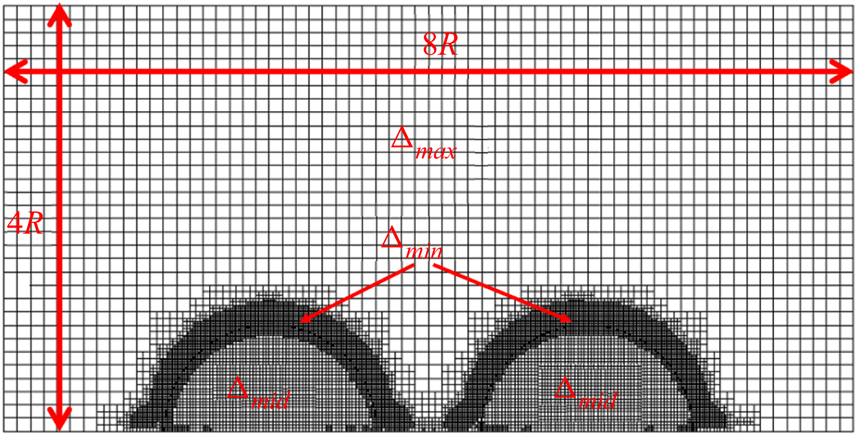
Figure 11. Schematic of initial computational domain.
Acknowledgement
We appreciate the experimental assistance of C.-J. Chang and C.-L. Hung.
Funding
We are grateful for the funding support of NTU Career Development Project (NTU-CDP-106R7822, NTU-107L7822, NTU-108L7822 and NTU-109L7822) and of MOST (109-2221-E-002-203 and 110-2221-E- 002-088-MY3).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Experimental methodology
The field of view and frame rate for every collision event depend on the droplet diameter and table 3 indicates the corresponding settings.
Table 3. Settings of high-speed camera.
Appendix B. Calculation of Hamaker constant
To estimate the critical thickness 
$({h_{cr}})$ between two drops, the Hamaker constants of various liquids are evaluated and listed in table 4. The quantities are calculated by the Lifshitz theory considering two identical masses of liquids in proximity in vacuum/air (Lifshitz Reference Lifshitz1956; Israelachvili Reference Israelachvili2011), showing that
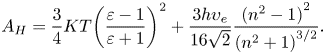\begin{equation}{A_H} = \frac{3}{4}KT{\left( {\frac{{\varepsilon - 1}}{{\varepsilon + 1}}} \right)^2} + \frac{{3h{\upsilon _e}}}{{16\sqrt 2 }}\frac{{{{({n^2} - 1)}^2}}}{{{{({n^2} + 1)}^{3/2}}}}.\end{equation}Table 4. Properties of tested liquids (25 °C).
Appendix C. Derivation of the momentum equation for the droplet
The momentum equation (3.2) is derived from the projection of the quasi-steady Navier–Stokes equation along the streamline (Spivak et al. Reference Spivak, Vanden-Broeck and Miloh2002), showing that
\begin{align}\frac{1}{\rho }\frac{{\partial P}}{{\partial s}} + {V_S}\frac{{\partial {V_s}}}{{\partial s}} + {V_n}\frac{{\partial {V_n}}}{{\partial n}} = V \times \omega - \nu (\nabla \times \omega ) = {V_z}{\omega _n} - {V_n}{\omega _z} - \nu \left( {\frac{{\partial {\omega_z}}}{{\partial n}} - \frac{{\partial {\omega_n}}}{{\partial z}}} \right).\end{align}
Here the subscript s denotes the direction along the streamline and n denotes the direction normal to the streamline. In the present scenario, 
${\omega _n} = {V_n} = {V_z} = 0$, and thus (C1) becomes
\begin{equation}\frac{1}{\rho }\frac{{\partial P}}{{\partial s}} + {V_S}\frac{{\partial {V_s}}}{{\partial s}} = \nu \frac{{\partial {\omega _z}}}{{\partial n}},\end{equation}or in dimensionless form
\begin{equation}\frac{{\partial \bar{P}}}{{\partial \bar{s}}} + \overline {{V_S}} \frac{{\partial \overline {{V_s}} }}{{\partial \bar{s}}} = \frac{1}{{R{e_l}}}\frac{{\partial \overline {{\omega _z}} }}{{\partial \bar{n}}}.\end{equation}
Here 
$R{e_l} = {\rho _l}UD/{\mu _l}$, which is the Reynolds number of the droplet. Based on the numerical simulation (figure 10), the magnitude of vorticity in the droplet is very small, which is at least 20 times smaller than that in the gas phase. In addition, since 
$1/R{e_l}\; < 0.05$ in the present study, we neglect 
$\nu (\partial {\omega _z}/\partial n)$ and (C2) becomes
\begin{equation}\frac{1}{\rho }\frac{{\partial P}}{{\partial s}} + {V_S}\frac{{\partial {V_s}}}{{\partial s}} = {\nabla _s}\left( {\frac{P}{\rho } + \frac{1}{2}V_s^2} \right) = 0.\end{equation}This result shows that the momentum equation with the viscous term has the same form as the Bernoulli equation when it is projected along the streamline. Thus we assume that the droplet is viscous while the Bernoulli equation is valid for describing the momentum distribution in the droplet.
Appendix D. Numerical setting of the simulation in Appendix C
To understand the vorticity distribution in the droplets during the bouncing process, here we reproduce a previous experimental case (Pan et al. Reference Pan, Law and Zhou2008) using GERRIS open source code (Popinet Reference Popinet2003, Reference Popinet2009). The initial computational domain of GERRIS axisymmetric simulation is shown in figure 11, where the centres of two identical droplets are placed on the symmetry axis with a separation distance of 3R, each given a velocity magnitude of U/2 but in opposite directions. The computational boundaries are set to have zero gradients for velocities, i.e. Neumann conditions, and fixed pressure at zero, i.e. Dirichlet conditions. The adaptive mesh refinement, with three different initial mesh sizes 
$({\varDelta _{max}},{\varDelta _{mid}},{\varDelta _{min}}) = (R/{2^3},R/{2^5},R/{2^6})$, is performed in the computations to facilitate numerical simulations, where 
${\varDelta _{max}}$ is set in the gas phase, 
${\varDelta _{min}}$ in the liquid–gas interface and 
${\varDelta _{mid}}$ in the liquid phase and high-vorticity region of the gas phase. To resolve the dynamics of the gas film, 
${\varDelta _{min}}$ is set to R/210 (166 nm). By using a Courant–Friedrichs–Lewy (CFL) number of 0.2 and the physical parameters as listed in table 5, the experimental results can be reproduced by the simulations with the same impact conditions, as shown in figure 10.
Table 5. Properties of tetradecane drops (25 °C).
Open access
