Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T02:30:23.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitional flow of a rarefied gas over a spinning sphere

Published online by Cambridge University Press:  15 September 2011

Alexey N. Volkov
Alexey N. Volkov*
Affiliation:
Department of Materials Science and Engineering, University of Virginia, 395 McCormick Road, Charlottesville, VA 22904-4745, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Three-dimensional transitional flow of a rarefied monatomic gas over a spinning sphere is studied numerically by the direct simulation Monte Carlo method. Gas molecules interact with each other as hard spheres. The Maxwell model of specular–diffuse scattering is used to describe the interaction between gas molecules and the sphere surface. The effect of all dimensionless governing parameters of the problem on the flow structure, distributions of stresses and heat flux density on the sphere surface, aerodynamic force and torque exerted on the sphere, and heat flux on the sphere surface is analysed. Simulations are conducted at Mach numbers raging from to 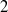and Knudsen numbers raging from 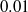to 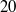. Two qualitatively different streamline patterns are observed around the sphere depending on its dimensionless rotational velocity. The direction and magnitude of the transverse Magnus force in transitional flow depend on the Knudsen and Mach numbers. The torque and heat flux coefficients are found to be functions of the Mach number and dimensionless rotational velocity. The effect of rotation on the sphere aerodynamics weakens with an increase in the sphere temperature with respect to the gas temperature in the free stream. A complete set of equations is developed to fit the computed values of the aerodynamic and heat flux coefficients in a case when the sphere temperature is equal to the temperature of the free stream.

JFM classification

Aerodynamics: Aerodynamics Compressible Flows: Compressible Flows Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 683 , 25 September 2011 , pp. 320 - 345
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arkilic, E. B., Breuer, K. S. & Schmidt, M. A. 2001 Mass flow and tangential momentum accommodation in silicon micromachined channels. J. Fluid Mech. 437, 29–43.CrossRefGoogle Scholar
2. Ashley, H. J. 1949 Applications of the theory of free molecule flow to aeronautics. J. Aeronaut. Sci. 16, 95–104.Google Scholar
3. Bagchi, P. & Balachandar, S. 2002 Effect of free rotation on motion of a solid sphere. Phys. Fluids 14, 2719–2737.Google Scholar
4. Bailey, A. B. & Hiatt, J. 1971 Free-flight measurements of sphere drag at subsonic, transonic, supersonic, and hypersonic speeds for continuum, transition, and near-free-molecular flow conditions. Tech. Rep. AEDC-TR-70-291, Arnold Engineering Development Center.Google Scholar
5. Barkla, H. M. & Auchterlonie, L. J. 1971 The Magnus or Robins effect on rotating spheres. J. Fluid Mech. 47, 437–448.Google Scholar
6. Bird, G. A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon.Google Scholar
7. Borg, K. I., Söderholm, L. H. & Essen, H. 2003 Force on a spinning sphere moving in a rarefied gas. Phys. Fluids 15, 736–741.Google Scholar
8. Burt, J. M. & Boyd, I. D. 2005 Particle rotation effects in rarefied two-phase plume flows. In 24th International Symposium on Rarefied Gas Dynamics (ed. Capitelli, M. ), pp. 413–418. AIP.Google Scholar
9. Cercignani, C. 1988 The Boltzmann Equation and its Applications. Springer.CrossRefGoogle Scholar
10. Chegroun, N. & Oesterle, B. 1993 Etude numérique de la trainée, de la portance et du couple sur une sphere en translation et en rotation. In Actes 11eme Congres Français Mécanique, vol. 3, pp. 81–84.Google Scholar
11. Crifo, J.-F., Loukianov, G. A., Rodionov, A. V. & Zakharov, V. V. 2005 Direct Monte Carlo and multifluid modeling of the circumnuclear dust coma: spherical grain dynamics revisited. Icarus 176, 192–219.CrossRefGoogle Scholar
12. Crowe, C. T., Sommerfeld, M. & Tsuji, Y. 1998 Multiphase Flows with Droplets and Particles. CRC.Google Scholar
13. Davies, J. M. 1949 The aerodynamics of golf balls. J. Appl. Phys. 20, 821–828.Google Scholar
14. Dennis, S. C. R., Singh, S. N. & Ingham, D. B. 1980 The steady flow due to a rotating sphere at low and moderate Reynolds numbers. J. Fluid Mech. 101, 257–279.Google Scholar
15. Filippov, A. V. & Rosner, D. E. 2000 Energy transfer between an aerosol particle and gas at high temperature ratios in the Knudsen transition regime. Intl J. Heat Mass Transfer 43, 127–138.CrossRefGoogle Scholar
16. Henderson, C. B. 1976 Drag coefficients of spheres in continuum and rarefied flows. AIAA J. 14, 707–708.CrossRefGoogle Scholar
17. Hirschfelder, J. O., Curtiss, C. F. & Bird, R. B. 1964 Molecular Theory of Gases and Liquids. Wiley.Google Scholar
18. Hurlbut, F. C. 1963 On the molecular interactions between gases and solids. In Dynamics of Manned Lifting Planetary Entry, pp. 754–777. Wiley.Google Scholar
19. Ivanov, S. G. & Yanshin, A. M. 1980 Forces and moments acting on bodies rotating about a symmetry axis in a free molecular flow (in Russian). Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza, No. 3, 151–155 (translation in Fluid Dyn. 15, 449–453).Google Scholar
20. Kavanau, L. L. 1955 Heat transfer from spheres to a rarefied gas in subsonic flow. Trans. ASME 77, 617–623.Google Scholar
21. Kim, D. & Choi, H. 2002 Laminar flow past a sphere rotating in the streamwise direction. J. Fluid Mech. 461, 365–386.Google Scholar
22. Kirchhoff, G. 1876 Vorlesungen Über Mathematische Physik: Mechanik. Teubner.Google Scholar
23. Kogan, M. N. 1969 Rarefied Gas Dynamics. Plenum.Google Scholar
24. Koshmarov, Y. A. & Svirshevskii, S. B. 1972 Heat transfer from a sphere in the intermediate dynamics region of a rarefied gas (in Russian). Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza, No. 2, 170–172 (translation in Fluid Dyn. 7, 343–346).CrossRefGoogle Scholar
25. Kutateladze, S. S. 1963 Fundamentals of Heat Transfer. Academic.Google Scholar
26. Lawrence, W. R. 1967Free-flight range measurements of sphere drag at low Reynolds numbers and low Mach numbers. Tech. Rep. AEDC-TR-67-218, Arnold Engineering Development Center.Google Scholar
27. Lim, H., Jang, D., Kim, D. & Lee, J. W. 2005 Correlation between particle removal and shock-wave dynamics in the laser shock cleaning process. J. Appl. Phys. 97, 054903–(1–6).Google Scholar
28. Loth, E. 2008 Lift of a solid spherical particle subject to vorticity and/or spin. AIAA J. 46, 801–809.Google Scholar
29. Maccoll, J. H. 1928 Aerodynamics of a spinning sphere. J. R. Aero. Soc. 32, 777–798.CrossRefGoogle Scholar
30. Maxwell, J. C. 1879 On stress in rarefied gases arising from inequalities of temperature. Phil. Trans. R. Soc. Lond. 170, 231–256 (reprinted in The Scientific Papers of James Clerk Maxwell, Dover).Google Scholar
31. Michaelides, E. E. 2006 Particles, Bubbles and Drops: Their Motion, Heat and Mass Transfer. World Scientific.Google Scholar
32. Nelson, H. F. & Fields, J. C. 1996 Heat transfer in two-phase solid-rocket plumes. J. Spacecr. Rockets 33, 494–500.CrossRefGoogle Scholar
33. Niazmand, H. & Renksizbulut, M. 2003 Surface effects on transient three-dimensional flows around rotating spheres at moderate Reynolds numbers. Comput. Fluids 32, 1405–1433.Google Scholar
34. Oesterle, B. & Bui Dinh, T. 1998 Experiments on the lift of a spinning sphere in a range of intermediate Reynolds numbers. Exp. Fluids 25, 16–22.Google Scholar
35. Padmapriyaand, P. & Reddy, K. P. J. 2001 Numerical analysis of dusty hypersonic viscous gas flow over a flat plate. AIAA J. 39 (7), 1313–1319.Google Scholar
36. Papadopoulos, P., Tauber, M. E. & Chang, I.-D. 1993 Heatshield erosion in a dusty Martian atmosphere. J. Spacecr. Rockets 30, 140–151.CrossRefGoogle Scholar
37. Porneala, C. & Willis, D. A. 2006 Observation of nanosecond laser-induced phase explosion in aluminum. Appl. Phys. Lett. 89, 211121–(1–3).Google Scholar
38. Rubinow, S. I. & Keller, J. B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11, 447–459.Google Scholar
39. Sakamoto, H. & Haniu, H. 1990 A study of vortex shedding from spheres in a uniform flow. J. Fluids Engng 112, 386–392.Google Scholar
40. Sauer, F. M. 1951 Convective heat transfer from spheres in free molecular flow. J. Aeronaut. Sci. 18, 353–354.Google Scholar
41. Sedov, L. I. 1993 Similarity and Dimensional Methods in Mechanics. CRC.Google Scholar
42. Tsuji, Y., Morikawa, Y. & Mizuno, O. 1985 Experimental measurements of the Magnus force on a rotating sphere at low Reynolds numbers. Trans. ASME: J. Fluids Engng 107, 484–488.Google Scholar
43. Vasilevskii, E. B., Osiptsov, A. N., Chirikhin, A. V. & Yakovleva, L. V. 2001 Heat exchange on the front surface of a blunt body in a high-speed flow containing low-inertia particles (in Russian). Inzhenerno-Fizicheskii Zhurnal 74, 29–37 (translation in J. Engng Phys. Thermophys. 74, 1399–1411).Google Scholar
44. Volkov, A. N. 2007aThe aerodynamic and heat properties of a spinning spherical particle in transitional flow. In 6th International Conference on Multiphase Flow (CD-ROM Proc. ICMF 2007), paper S2_Mon_C_6, Martin-Luther-Universität Halle-Wittenberg.Google Scholar
45. Volkov, A. N. 2007b Numerical modelling of the Magnus force and the aerodynamic torque on a spinning sphere in transitional flow. In 25th International Symposium on Rarefied Gas Dynamics (ed. Ivanov, M. & Rebrov, A. ), pp. 771–776. SBRAS.Google Scholar
46. Volkov, A. N. 2009 Aerodynamic coefficients of a spinning sphere in a rarefied-gas flow (in Russian). Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 1, 167–187 (translation in Fluid Dyn. 44, 141–157).Google Scholar
47. Wang, C.-T. 1972 Free molecular flow over a rotating sphere. AIAA J. 10, 713–714.Google Scholar
48. Weidman, P. D. & Herczynski, A. 2004 On the inverse Magnus effect in free molecular flow. Phys. Fluids 16, L9–L12.Google Scholar
49. Zarin, N. A. 1970Measurement of non-continuum and turbulence effects on subsonic sphere drag. Tech. Rep. CR-1585, NASA.Google Scholar
Supplementary material: PDF

Volkov supplemtary material

Supplementary material

Download Volkov supplemtary material(PDF)
PDF 571.6 KB