Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-09T18:55:25.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to turbulence through steep global-modes cascade in an open rotating cavity

Published online by Cambridge University Press:  28 October 2011

Bertrand Viaud ,
Eric Serre  and
Jean-Marc Chomaz
Bertrand Viaud*
Affiliation:
Centre de Recherche de l’Armée de l’Air, CReA BA701 13661 Salon de Provence, France M2P2, CNRS Universités Aix Marseille, IMT Chateau-Gombert 13451 Marseille, France
Eric Serre
Affiliation:
M2P2, CNRS Universités Aix Marseille, IMT Chateau-Gombert 13451 Marseille, France
Jean-Marc Chomaz
Affiliation:
LadHyX, CNRS-Ecole Polytechnique, F-91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The transition to turbulence in a rotating boundary layer is analysed via direct numerical simulation (DNS) in an annular cavity made of two parallel corotating discs of finite radial extent, with a forced inflow at the hub and free outflow at the rim. In a former numerical investigation (Viaud, Serre & Chomaz J. Fluid Mech., vol. 598, 2008, pp. 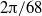451–464) realized in a sectorial cavity of azimuthal extent , we have established the existence of a primary bifurcation to nonlinear global mode with angular phase velocity and radial envelope coherent with the so-called elephant mode theory. The former study has demonstrated the subcritical nature of this primary bifurcation with a base flow that keeps being linearly stable for all Reynolds numbers studied. The present work investigates the stability of this elephant mode by extending the cavity both in the radial and azimuthal direction. When the Reynolds number based on the forced throughflow is increased above a threshold value for the existence of the nonlinear global mode, a large-amplitude impulsive perturbation gives rise to a self-sustained saturated wave with characteristics identical to the 68-fold global elephant mode obtained in the smaller cavity. This saturated wave is itself globally unstable and a second front appears in the lee of the primary where small-scale instability develops. These secondary instabilities are identical for the 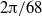and the 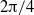long sectorial cavities, indicating that transition involves a Floquet mode of zero azimuthal wavenumber. This secondary instability leads to a very disorganized state, defining the transition to turbulence. The observed transition to turbulence linked to the secondary instability of a global mode confirms, for the first time on a real flow, the possibility of a direct transition to turbulence through an elephant mode cascade, a scenario that was up to now only observed on the Ginzburg–Landau model.

JFM classification

Instability: Absolute/convective instability Boundary Layers: Boundary layer stability Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 688 , 10 December 2011 , pp. 493 - 506
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Akervik, E., Brandt, L., Henningson, D. S. & Hoepffner, J. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 126602.CrossRefGoogle Scholar
2. Crespo del Arco, E., Serre, E., Bontoux, P. & Launder, B. E. 2005 Stability, transition and turbulence in rotating cavities. In Advances in Fluid Mechanics (ed. Rahman, M. ). Dalhousie University Canada Series , vol. 41. pp. 141–196. WIT Press.Google Scholar
3. Chomaz, J. M. 1992 Absolute and convective instabilities in nonlinear system. Phys. Rev. Lett. 69, 1931–1934.CrossRefGoogle Scholar
4. Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1991 A frequency selection criterion in spatially developping flows. Stud. Appl. Maths 84, 119–144.CrossRefGoogle Scholar
5. Couairon, A. & Chomaz, J. M. 1999 Primary and secondary nonlinear global instability. Physica D 132, 428–456.CrossRefGoogle Scholar
6. Davies, C. & Carpenter, P. W. 2003 Global behaviour corresponding to the absolute instability of the rotating-disk boundary layer. J. Fluid Mech. 486, 287–329.CrossRefGoogle Scholar
7. Davies, C., Thomas, C. & Carpenter, P. W. 2007 Global stability of the rotating-disk boundary layer. J. Engng Maths 57, 219–236.CrossRefGoogle Scholar
8. Gollub, J. P. & Swinney, Harry L. 1975 Onset of turbulence in a rotating fluid. Phys. Rev. Lett. 35 (14), 927–930.CrossRefGoogle Scholar
9. Hide, R. 1968 On source-sink flows stratified in a rotating annulus. J. Fluid Mech. 32, 737–764.CrossRefGoogle Scholar
10. Huerre, P. 1988 On the absolute/convective nature of primary and secondary instabilities. In Propagation in System Far from Equilibrium (ed. Wesfreid, J. E., Brand, H. R., Manneville, P., Albinet, G. & Boccara, N. ). pp. 340–353. Springer.CrossRefGoogle Scholar
11. Lingwood, R. J. 1995 Absolute instability of the boundary layer on a rotating disk. J. Fluid Mech. 299, 17–33.CrossRefGoogle Scholar
12. Lingwood, R. J. 1996 An experimental study of the absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.CrossRefGoogle Scholar
13. Lingwood, R. J. 1997 Absolute instability of the Ekman layer and related rotating flows. J. Fluid Mech. 331, 405–428.CrossRefGoogle Scholar
14. Owen, J. M. & Pincombe, J. R. 1980 Velocity-measurements inside a rotating cylindrical cavity with a radial outflow of fluid. J. Fluid Mech. 99, 111–127.CrossRefGoogle Scholar
15. Owen, J. M. & Rogers, R. H. 1995 Heat Transfer in Rotating-disk System. Wiley.Google Scholar
16. Perret, G., Stegner, A., Dubos, T., Chomaz, J. M. & Farge, M. 2006 Stability of parallel wake flows in quasigeostrophic and frontal regimes. Phys. Fluids 18, 126602.CrossRefGoogle Scholar
17. Pier, B. 2003 Finite amplitude crossflow vortices, secondary instability and transition in the rotating-disk boundary layer. J. Fluid Mech. 487, 315–343.CrossRefGoogle Scholar
18. Pier, B., Huerre, P., Chomaz, J. M. & Couairon, A. 1998 Steep nonlinear global modes in spatially developing media. Phys. Fluids 10, 2433–2435.CrossRefGoogle Scholar
19. Serre, E., Hugues, S., Crespo del Arco, E., Randriamampianina, A. & Bontoux, P. 2001 Axisymmetric and three-dimensional instabilities in an Ekman boundary-layer flow. Intl J. Heat. Transfer Fluid Flow 22, 82–93.CrossRefGoogle Scholar
20. Severac, E. & Serre, E. 2007 A spectral vanishing viscosity for the les of turbulent flows within rotating cavities. J. Comput. Phys. 226, 1234–1255.CrossRefGoogle Scholar
21. Tobias, S. M., Proctor, M. R. E. & Knobloch, E. 1998 Convective and absolute instabilities of fluid flows in finite geometry. Physica D 113, 43–72.CrossRefGoogle Scholar
22. Viaud, B., Serre, E. & Chomaz, J. M. 2008 The elephant mode between two rotating disks. J. Fluid Mech. 598, 451–464.CrossRefGoogle Scholar
23. Zandbergen, P. J. & Dijkstra, D. 1986 Vonkármán swirling flows. Annu. Rev. Fluid Mech. 19, 465–491.CrossRefGoogle Scholar