Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T21:34:36.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to turbulence in toroidal pipes

Published online by Cambridge University Press:  18 October 2011

Ivan Di Piazza  and
Michele Ciofalo
Ivan Di Piazza
Affiliation:
Dipartimento dell’Energia, Università degli Studi di Palermo, Viale delle Scienze, I-90128 Palermo, Italy
Michele Ciofalo*
Affiliation:
Dipartimento dell’Energia, Università degli Studi di Palermo, Viale delle Scienze, I-90128 Palermo, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Incompressible flow in toroidal pipes of circular cross-section was investigated by three-dimensional, time-dependent numerical simulations using a finite volume method. The computational domain included a whole torus and was discretized by up to 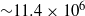nodes. Two curvatures 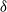(radius of the cross-section/radius of the torus), namely 0.3 and 0.1, were examined; a streamwise forcing term was imposed, and its magnitude was made to vary so that the bulk Reynolds number ranged between 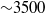and 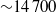. The results were processed by different techniques in order to confirm the spatio-temporal structure of the flow. Consecutive transitions between different flow regimes were found, from stationary to periodic, quasi-periodic and chaotic flow. At low Reynolds number, stationary flow was predicted, exhibiting a symmetric couple of Dean vortex rings and a strong shift of the streamwise velocity maximum towards the outer wall. For 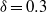, between 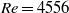and 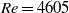a first transition occurred from stationary to periodic flow, associated with a supercritical Hopf bifurcation and giving rise to a travelling wave which took the form of a varicose streamwise modulation of the Dean vortex ring intensity. A further transition, associated with a secondary Hopf bifurcation, occurred between 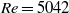and 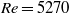and led to a quasi-periodic flow characterized by two independent fundamental frequencies associated with distinct travelling waves, the first affecting mainly the Dean vortex rings and similar to that observed in purely periodic flow, the second localized mainly in the secondary flow boundary layers and manifesting itself as an array of oblique vortices produced at the edge of the Dean vortex regions. Both the periodic and the quasi-periodic regimes were characterized by an instantaneous anti-symmetry of the oscillatory components with respect to the equatorial midplane of the torus. For 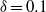, between 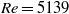and 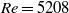a direct (‘hard’) transition from steady to quasi-periodic flow occurred. Hysteresis was also observed: starting from a quasi-periodic solution and letting the Reynolds number decrease, both quasi-periodic and periodic stable solutions were obtained at Reynolds numbers below the critical value. A further decrease in 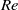led to steady-state solutions. This behaviour suggests the existence of a subcritical Hopf bifurcation followed by a secondary Hopf bifurcation. The resulting periodic and quasi-periodic flows were similar to those observed for the higher curvature, but the travelling modes were now instantaneously symmetric with respect to the equatorial midplane of the torus. Also, the further transition from quasi-periodic to chaotic flow occurred with different modalities for the two curvatures. For 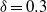, a centrifugal instability of the main flow in the outer region occurred abruptly between 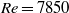and 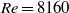, while a further increase of 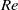up to 13 180 did not cause any relevant change in the distribution and intensity of the fluctuations. For the transition to chaotic flow was gradual in the range 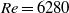to 8160 and affected mainly the inner region; only a further increase of 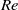to 14 700 caused fluctuations to appear also in the outer region.

JFM classification

Boundary Layers: Pipe flow boundary layer Instability: Transition to turbulence Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 687 , 25 November 2011 , pp. 72 - 117
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Current address: ENEA UTIS-TCI, C.R. Brasimone, 40032 Camugnano(Bo), Italy.

References

1. Avila, M., Meseguer, A. & Marques, F. 2006 Double Hopf bifurcation in corotating spiral Poiseuille flow. Phys. Fluids 18, 064101.CrossRefGoogle Scholar
2. Barua, S. N. 1963 On the secondary flow in stationary curved pipes. Q. J. Mech. Appl. Math. 16, 61–77.CrossRefGoogle Scholar
3. Berger, S. A., Talbot, L. & Yao, L. S. 1983 Flow in curved pipes. Ann. Rev. Fluid Mech. 15, 461–512.CrossRefGoogle Scholar
4. Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
5. Boussinesq, M. J. 1868 Mémoire sur l’influence des frottements dans les mouvements régulier des fluids. J. Math. Pures Appl. 2me Sér. 13, 377–424.Google Scholar
6. Chandrasekar, S. 1970 Hydrodynamic and Hydromagnetic Stability, 3rd printing. Oxford University Press.Google Scholar
7. Chen, W. H. & Jan, R. 1992 The characteristics of laminar flow in a helical circular pipe. J. Fluid Mech. 244, 241–256.CrossRefGoogle Scholar
8. Choi, H. & Moin, P. 1994 Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 113, 1–4.CrossRefGoogle Scholar
9. Cioncolini, A. & Santini, L. 2006 An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 30, 367–380.CrossRefGoogle Scholar
10. Collins, W. M. & Dennis, S. C. R. 1975 The steady motion of a viscous fluid in a curved tube. Q. J. Mech. Appl. Math. 28, 133–156.CrossRefGoogle Scholar
11. Daskopoulos, P. & Lenhoff, A. M. 1989 Flow in curved ducts: bifurcation structure for stationary ducts. J. Fluid Mech. 203, 125–148.CrossRefGoogle Scholar
12. Dean, W. R. 1927 Note on the motion of the fluid in a curved pipe. Phil. Mag. 4, 208–223.CrossRefGoogle Scholar
13. Del Pino, C., Hewitt, R. E., Clarke, R. J., Mullin, T. & Denier, J. P. 2008 Unsteady fronts in the spin-down of a fluid-filled torus. Phys. Fluids 20, 124104.CrossRefGoogle Scholar
14. Dennis, S. C. R. & Ng, M. 1982 Dual solution for steady laminar flow through a curved tube. Q. J. Mech. Appl. Math. 35, 305–324.CrossRefGoogle Scholar
15. Einstein, A. 1926 Die Ursache der Mäanderbildung der Flußläufe und des sogenannten Baerschen Gesetzes. Naturwissenschaften 11, 223–224.CrossRefGoogle Scholar
16. Eustice, J. 1911 Experiment of streamline motion in curved pipes. Proc. R. Soc. Lond. A 85, 119–131.Google Scholar
17. Fenstermacher, P. R., Swinney, H. L. & Gollub, J. P. 1979 Dynamic instability and the transition to chaotic Taylor vortex flow. J. Fluid Mech. 94, 103–128.CrossRefGoogle Scholar
18. Friedrich, R., Hüttl, T. J., Manhart, M. & Wagner, C. 2001 Direct numerical simulation of incompressible turbulent flows. Comput. Fluids 30, 555–579.CrossRefGoogle Scholar
19. Fusegi, T., Hyun, J. M. & Kuwahara, K. 1992 Three-dimensional numerical simulation of periodic natural convection in a differentially heated cubical enclosure. Appl. Sci. Res. 49, 271–282.CrossRefGoogle Scholar
20. Germano, M. 1982 On the effect of torsion in a helical pipe flow. J. Fluid Mech. 125, 1–8.CrossRefGoogle Scholar
21. Gollub, J. P. & Benson, S. V. 1980 Many routes to turbulent convection. J. Fluid Mech. 100, 449–470.CrossRefGoogle Scholar
22. Grindley, J. H. & Gibson, A. H. 1908 On the frictional resistance to the flow of air through a pipe. Proc. R. Soc. Lond. A 80, 114–139.Google Scholar
23. Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proc. 1988 Summer Program, Report CTR-S88. NASA Center for Turbulence Research.Google Scholar
24. Hüttl, T. J. & Friedrich, R. 2001 Direct numerical simulation of turbulent flows in curved and helically coiled pipes. Comput. Fluids 30, 591–605.CrossRefGoogle Scholar
25. Hüttl, T. J., Chauduri, M., Wagner, C. & Friedrich, R. 2004 Reynolds-stress balance equations in orthogonal helical coordinates and application. Z. Angew. Math. Mech. 84, 403–416.CrossRefGoogle Scholar
26. Ito, H. 1959 Friction factors for turbulent flow in curved pipes. Trans. ASME: J. Basic Engng. 81, 123–134.CrossRefGoogle Scholar
27. Jayanti, S. & Hewitt, G. F. 1991 On the par adox concerning friction factor ratio in laminar flow in coils. Proc. R. Soc. Lond. Ser. A 432, 291–299.Google Scholar
28. Jinsuo, Z. & Benzhao, Z. 1999 Fluid flow in a helical pipe. Acta Mechanica Sin. 15, 299–312.CrossRefGoogle Scholar
29. Kao, H. C. 1987 Torsion effect on fully developed flow in a helical pipe. J. Fluid Mech. 184, 335–356.CrossRefGoogle Scholar
30. Kerswell, R. R. 2005 Recent progress in understanding the transition to turbulence in a pipe. Nonlinearity 18, R17–R44.CrossRefGoogle Scholar
31. Knightly, G. H. & Sather, D. 1993 Periodic waves in rotating plane Couette flow. Z. Angew. Math. Phys. 44, 1–16.CrossRefGoogle Scholar
32. Larrain, J. & Bonilla, C. F. 1970 Theoretical analysis of pressure drop in the laminar flow of fluid in a coiled pipe. Trans. Soc. Rheol. 14, 135–147.CrossRefGoogle Scholar
33. Lumley, J. L. 1967 The structure of inhomogeneous turbulence. In Atmospheric Turbulence and Wave Propagation (ed. A. M. Monin & V. I. Tatarski), pp. 166–178. Nauka.Google Scholar
34. McConalogue, D. J. & Srivastava, R. S. 1968 Motion of fluid in a curved tube. Proc. R. Soc. Lond. A 307, 37–53.Google Scholar
35. Mees, P. A. J., Nandakumar, K. & Masliyah, J. H. 1996 Secondary instability of flow in a curved duct of square cross-section. J. Fluid Mech. 323, 387–409.CrossRefGoogle Scholar
36. Mori, Y. & Nakayama, W. 1965 Study on forced convective heat transfer in curved pipes. Intl J. Heat Mass Transfer 8, 67–82.Google Scholar
37. Naphon, P. & Wongwises, S. 2006 A review of flow and heat transfer characteristics in curved tubes. Renewable and Sustainable Energy Rev. 10, 463–490.CrossRefGoogle Scholar
38. Narasimha, R. & Sreenivasan, K. R. 1979 Relaminarization of fluid flows. Adv. Appl. Mech. 19, 221–309.CrossRefGoogle Scholar
39. Rayleigh, Lord 1920 On the dynamics of revolving fluids. Scientific Papers 6, 447–453.Google Scholar
40. Siggers, J. H. & Waters, S. L. 2008 Unsteady flows in pipes with finite curvatures. J. Fluid Mech. 600, 133–165.CrossRefGoogle Scholar
41. Sreenivasan, K. R. & Strykowski, P. J. 1983 Stabilization effects in flow through helically coiled pipes. Exp. Fluids 1, 31–36.CrossRefGoogle Scholar
42. Srinivasan, S., Nadapurkar, S. & Holland, F. A. 1970 Friction factors for coils. Trans. Inst. Chem. Engrs 48, T 156–T 161.Google Scholar
43. Taylor, G. I. 1929 The criterion for turbulence in curved pipes. Proc. R. Soc. 124 (794), 243–249.Google Scholar
44. Thomson, J. 1876 On the origin of windings of rivers in alluvial plains, with remarks on the flow of water round bends in pipes. Proc. R. Soc. Lond. A 25, 5–8.Google Scholar
45. Van Dyke, M. 1978 Extended Stokes series: laminar flow through a loosely curved pipe. J. Fluid Mech. 86, 129–145.Google Scholar
46. Vashisth, S., Kumar, V. & Nigam, D. P. K. 2008 A review on the potential application of curved geometries in process industry. Ind. Engng Chem. Res. 47, 3291–3337.CrossRefGoogle Scholar
47. Wang, L. & Yang, T. 2004 Bifurcation and stability of forced convection in curved ducts of square cross-section. Intl J. Heat Mass Transfer 47, 2971–2987.CrossRefGoogle Scholar
48. Webster, D. R. & Humphrey, J. A. C. 1993 Experimental observations of flow instability in a helical coil. Trans. ASME: J. Fluids Engng 115, 436–443.Google Scholar
49. Webster, D. R. & Humphrey, J. A. C. 1997 Travelling wave instability in helical coil flow. Phys. Fluids 9, 407–418.CrossRefGoogle Scholar
50. White, C. M. 1929 Flow through curved pipes. Proc. R. Soc. 123 (792), 645–663.Google Scholar
51. Williams, G. S., Hubbell, C. W. & Fenkell, G. H. 1902 On the effect of curvature upon the flow of water in pipes. Trans. ASCE 47, 1–196.Google Scholar
52. Xie, G. D. 1990 Torsion effect on secondary flow in helical pipes. Intl J. Heat Fluid Flow 11, 114–119.CrossRefGoogle Scholar
53. Yamamoto, K., Akita, T., Ikeuki, H. & Kita, Y. 1995 Experimental study of the flow in a helical circular tube. Fluid Dynam. Res. 16, 237–249.Google Scholar
54. Yanase, S., Goto, N. & Yamamoto, K. 1989 Dual solution of the flow through a curved pipe. Fluid Dynam. Res. 5, 191–201.CrossRefGoogle Scholar
55. Yanase, S., Yamamoto, K. & Yoshida, T. 1994 Effect of curvature on dual solutions of flow through a curved circular tube. Fluid Dynam. Res. 13, 217–228.CrossRefGoogle Scholar
56. Zabielski, L. & Mestel, A. J. 1998 Steady flow in a helically symmetric pipe. J. Fluid Mech. 370, 297–320.CrossRefGoogle Scholar