Published online by Cambridge University Press: 11 November 2014
Results of direct numerical simulations of the transitional processes that characterise the evolution of a breaking internal gravity wave to a fully developed and essentially steady turbulent patch are presented. The stationary lee wave was forced by the imposition of an appropriate bottom boundary shape within a density-stratified domain having a uniform upstream velocity and density gradient, and with the ratio of momentum to thermal (or other) diffusivity defined by 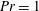 $\mathit{Pr}=1$. An earlier paper considered the eventual, fully developed turbulent patch arising after the breaking process is complete (Yakovenko et al., J. Fluid Mech., vol. 677, 2011, pp. 103–133); the focus in this paper is on the instabilities in the breaking process itself. The flow is analysed using streamlines, density contours and temporal and spatial spectra, as well as second moments of the velocity and density fluctuations, for a Reynolds number of 4000 based on the height of the bottom topography and the upstream velocity. The computations (on a grid using in excess of
$\mathit{Pr}=1$. An earlier paper considered the eventual, fully developed turbulent patch arising after the breaking process is complete (Yakovenko et al., J. Fluid Mech., vol. 677, 2011, pp. 103–133); the focus in this paper is on the instabilities in the breaking process itself. The flow is analysed using streamlines, density contours and temporal and spatial spectra, as well as second moments of the velocity and density fluctuations, for a Reynolds number of 4000 based on the height of the bottom topography and the upstream velocity. The computations (on a grid using in excess of 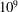 $10^{9}$ mesh points) yielded sufficient resolution to capture the fine-scale transition processes as well as the subsequent fully developed turbulence discussed earlier. It is shown that the major instability is of Rayleigh–Taylor type (RTI) with a resulting mixing region depth growing in a manner consistent with more classical RTI studies, despite the much more complicated environment. The resolution was sufficient to capture secondary Kelvin–Helmholtz-type instabilities on the developing RTI structures. Overall evolution towards the fully turbulent state characterised by a significant region of
$10^{9}$ mesh points) yielded sufficient resolution to capture the fine-scale transition processes as well as the subsequent fully developed turbulence discussed earlier. It is shown that the major instability is of Rayleigh–Taylor type (RTI) with a resulting mixing region depth growing in a manner consistent with more classical RTI studies, despite the much more complicated environment. The resolution was sufficient to capture secondary Kelvin–Helmholtz-type instabilities on the developing RTI structures. Overall evolution towards the fully turbulent state characterised by a significant region of 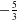 $-\frac{5}{3}$ subrange in both velocity and density spectra is very rapid. It is much faster than the long time scale characterising the subsequent evolution of the turbulent patch; this latter time scale is sufficiently large that the turbulent patch can itself be viewed as essentially steady.
$-\frac{5}{3}$ subrange in both velocity and density spectra is very rapid. It is much faster than the long time scale characterising the subsequent evolution of the turbulent patch; this latter time scale is sufficiently large that the turbulent patch can itself be viewed as essentially steady.