No CrossRef data available.
Article contents
Transition induced by a bursting vortex ring in channel flow
Published online by Cambridge University Press: 08 May 2024
Abstract
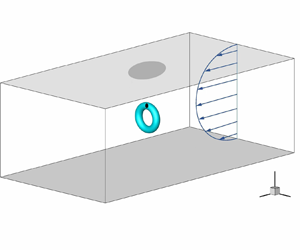
We investigate the influence of vortices remote from the boundary on the near-wall flow dynamics in wall-bounded flows. A vortex ring with precisely controlled local twist is introduced into the outer layer of a channel flow at a moderate Reynolds number. We find that the minimum vorticity flux for triggering the transition to turbulence is significantly reduced from the initial disturbance of an untwisted vortex ring to that of a twisted ring. In particular, the latter disturbance can cause vortex bursting in the early transitional stage. The impact of vortex bursting on the transition process is characterised by the near-wall, wall-normal velocity with the rapid distortion theory. The wall-normal velocity grows during vortex bursting, and leads to streak formation and then the transition to turbulence. The notable wall-normal velocity is induced by the large di-vorticity generated in vortex bursting. We model the growing radial component of the di-vorticity in terms of the local twist, and demonstrate that its surge is due to the generation of highly twisted vortex lines in vortex bursting. Then, we derive that the generation of the di-vorticity in the outer layer enhances the wall-normal velocity in the inner layer via the Poisson equation with the image method and the multipole expansion. Thus, we elucidate that the vortex bursting can have an effect on the transition process.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press



