Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-08T10:05:25.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition delay in a boundary layer flow using active control

Published online by Cambridge University Press:  15 August 2013

Onofrio Semeraro ,
Shervin Bagheri ,
Luca Brandt  and
Dan S. Henningson
Onofrio Semeraro*
Affiliation:
KTH Mechanics, Linné Flow Centre, Swedish e-Science Research Centre (SeRC), SE-100 44 Stockholm, Sweden
Shervin Bagheri
Affiliation:
KTH Mechanics, Linné Flow Centre, Swedish e-Science Research Centre (SeRC), SE-100 44 Stockholm, Sweden
Luca Brandt
Affiliation:
KTH Mechanics, Linné Flow Centre, Swedish e-Science Research Centre (SeRC), SE-100 44 Stockholm, Sweden
Dan S. Henningson
Affiliation:
KTH Mechanics, Linné Flow Centre, Swedish e-Science Research Centre (SeRC), SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Active linear control is applied to delay the onset of laminar–turbulent transition in the boundary layer over a flat plate. The analysis is carried out by numerical simulations of the nonlinear, transitional regime. A three-dimensional, localized initial condition triggering Tollmien–Schlichting waves of finite amplitude is used to numerically simulate the transition to turbulence. Linear quadratic Gaussian controllers based on reduced-order models of the linearized Navier–Stokes equations are designed, where the wall sensors and the actuators are localized in space. A parametric analysis is carried out in the nonlinear regime, for different disturbance amplitudes, by investigating the effects of the actuation on the flow due to different distributions of the localized actuators along the spanwise direction, different sizes of the actuators and the effort of the controllers. We identify the range of parameters where the controllers are effective and highlight the limits of the device for high amplitudes and strong control action. 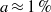Despite the fully linear control approach, it is shown that the device is effective in delaying the onset of laminar–turbulent transition in the presence of packets characterized by amplitudes $a\approx 1\hspace{0.167em} \% $ of the free stream velocity at the actuator location. Up to these amplitudes, it is found that a proper choice of the actuators positively affects the performance of the controller. For a transitional case, 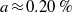$a\approx 0. 20\hspace{0.167em} \% $, we show a transition delay of 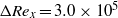$\Delta {\mathit{Re}}_{x} = 3. 0\times 1{0}^{5} $.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer control Flow Control: Flow Control Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 288 - 311
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
©2013 Cambridge University Press.

References

Adams, N. & Stolz, S. 1999 On the approximate deconvolution procedure for LES. Phys. Fluids 2, 1699–1701.Google Scholar
Åkervik, E., Hœpffner, J., Ehrenstein, U. & Henningson, D. S. 2007 Optimal growth, model reduction and control in a separated boundary-layer flow using global eigenmodes. J. Fluid. Mech. 579, 305–314.Google Scholar
Anderson, B. & Liu, Y. 1989 Controller reduction: concepts and approaches. IEEE Trans. Autom. Control 34, 802–812.Google Scholar
Andersson, P., Berggren, M. & Henningson, D. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11, 134–150.Google Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.Google Scholar
Bagheri, S., Brandt, L. & Henningson, D. S. 2009a Input–output analysis, model reduction and control design of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.Google Scholar
Bagheri, S. & Henningson, D. S. 2011 Transition delay using control theory. Phil. Trans. R. Soc. A 369, 1365–1381.Google Scholar
Bagheri, S., Hœpffner, J., Schmid, P. J. & Henningson, D. S. 2009b Input–output analysis and control design applied to a linear model of spatially developing flows. Appl. Mech. Rev. 62 (2), 020803.Google Scholar
Barbagallo, A., Sipp, D. & Schmid, P. 2009 Closed-loop control of an open cavity flow using reduced order models. J. Fluid Mech. 641, 1–50.Google Scholar
Belson, B., Semeraro, O., Rowley, C. & Henningson, D. 2013 Feedback control of instabilities in the two-dimensional Blasius boundary layer: the role of sensors and actuators. Phys. Fluids 25, 054106.Google Scholar
Bewley, T. R. & Liu, S. 1998 Optimal and robust control and estimation of linear paths to transition. J. Fluid Mech. 365, 305–349.CrossRefGoogle Scholar
Brandt, L., Sipp, D., Pralits, J. O. & Marquet, O. 2011 Effect of base-flow variation in noise amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.Google Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S. 2007 A pseudo spectral solver for incompressible boundary layer flows. In Trita-Mek 7. KTH Mechanics, Stockholm, Sweden.Google Scholar
Cortelezzi, L., Speyer, J. L., Lee, K. H. & Kim, J. 1998 Robust reduced-order control of turbulent channel flows via distributed sensors and actuators. In IEEE 37th Conference of Decision Control, pp. 1906–1911.Google Scholar
Doyle, J. C., Glover, K., Khargonekar, P. P. & Francis, B. A. 1989 State-space solutions to standard ${H}_{2} $ and ${H}_{\infty } $ control problems. IEEE Trans. Autom. Control 34, 831–847.Google Scholar
Dullerud, E. G. & Paganini, F. 1999 A Course in Robust Control Theory. A Convex Approach. Springer.Google Scholar
Glad, T. & Ljung, L. 2001 Control Theory - Multivariable and Nonlinear Methods. Taylor and Francis.Google Scholar
Grundmann, S. & Tropea, C. 2008 Active cancellation of artificially introduced Tollmien–Schlichting waves using plasma actuators. Exp. Fluids 44 (5), 795–806.Google Scholar
Henningson, D. S., Lundbladh, A. & Johansson, A. V. 1993 A mechanism for bypass transition from localized disturbances in wall-bounded shear flows. J. Fluid Mech. 250, 169–207.Google Scholar
Hervé, A., Sipp, D., Schmid, P. J. & Samuelides, M. 2012 A physics-based approach to flow control using system identification. J. Fluid Mech. 702, 26–58.Google Scholar
Ilak, M. & Rowley, C. W. 2008 Modelling of transitional channel flow using balanced proper orthogonal decomposition. Phys. Fluids 20, 034103.Google Scholar
Joshi, S. S., Speyer, J. L. & Kim, J. 1997 A systems theory approach to the feedback stabilization of infinitesimal and finite-amplitude disturbances in plane Poiseuille flow. J. Fluid Mech. 332, 157–184.Google Scholar
Juang, J. & Pappa, R. S. 1985 An eigensystem realization algorithm for modal paramter identification and model reduction. J. Guid. Control. Dyn. 3 (25), 620–627.Google Scholar
Juillet, F., Schmid, P. J. & Huerre, P. 2013 Control of amplifier flows using subspace identification techniques. J. Fluid Mech. 725, 522–565.Google Scholar
Kachanov, Y. S. 1994 Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech 26 (1), 411–482.Google Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.Google Scholar
Kriegseis, J. 2011 Performance characterization and quantification of dielectric barrier discharge plasma actuators. PhD thesis, TU Darmstadt.Google Scholar
Lewis, F. L. & Syrmos, L. V. 1995 Optimal Control. John Wiley and Sons.Google Scholar
Li, Y. & Gaster, M. 2006 Active control of boundary-layer instabilities. J. Fluid Mech. 550, 185–205.Google Scholar
Lundell, F. 2007 Reactive control of transition induced by free stream turbulence: an experimental demonstration. J. Fluid Mech. 585, 41–71.CrossRefGoogle Scholar
Ma, Z., Ahuja, S. & Rowley, C. W. 2011 Reduced order models for control of fluids using the Eigensystem Realization Algorithm. Theoret. Comput. Fluid Dyn. 25 (1), 233–247.Google Scholar
Monokrousos, A., Åkervik, E., Brandt, L. & Henningson, D. S. 2010 Global optimal disturbances in the Blasius boundary-layer flow using time steppers. J. Fluid Mech. 650, 181–214.Google Scholar
Monokrousos, A., Brandt, L., Schlatter, P. & Henningson, D. S. 2008 DNS and LES of estimation and control of transition in boundary layers subject to free stream turbulence. Intl J. Heat Fluid Flow 29 (3), 841–855.Google Scholar
Moore, B. 1981 Principal component analysis in linear systems: controllability, observability, and model reduction. IEEE Trans. Automat. Control 26 (1), 17–32.Google Scholar
Nordström, J., Nordin, N. & Henningson, D. S. 1999 The fringe region technique and the Fourier method used in the direct numerical simulation of spatially evolving viscous flows. SIAM J. Sci. Comput. 20 (4), 1365–1393.Google Scholar
Rowley, C. W. 2005 Model reduction for fluids using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15 (3), 997–1013.Google Scholar
Rowley, C. & Juttijudata, W. 2005 Model-based control and estimation of cavity flow oscillations. In 44th IEEE Conference on Decision and Control, pp. 512–517.Google Scholar
Schlatter, P., Stolz, S. & Kleiser, L. 2004 LES of transitional flows using the approximate deconvolution model. Intl J. Heat Fluid Flow 25 (3), 549–558.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Semeraro, O., Bagheri, S., Brandt, L. & Henningson, D. S. 2011 Feedback control of three-dimensional optimal disturbances using reduced-order models. J. Fluid Mech. 677, 63–102.Google Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 30801.Google Scholar
Skogestad, S. & Postlethwaite, I. 2005 Multivariable Feedback Control, Analysis to Design, 2nd edn. Wiley.Google Scholar
Sturzebecher, D. & Nitsche, W. 2003 Active cancellation of Tollmien–Schlichting waves instabilities on a wing using multi-channel sensor actuator systems. Intl J. Heat Fluid Flow 24, 572–583.Google Scholar