Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-07-03T04:28:51.846Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition and turbulence in horizontal convection: linear stability analysis

Published online by Cambridge University Press:  16 May 2017

Pierre-Yves Passaggia Open the ORCID record for Pierre-Yves Passaggia [Opens in a new window] ,
Alberto Scotti Open the ORCID record for Alberto Scotti [Opens in a new window]  and
Brian White
Pierre-Yves Passaggia*
Affiliation:
Department of Marine Sciences, University of North Carolina, Chapel Hill, NC 27599, USA
Alberto Scotti
Affiliation:
Department of Marine Sciences, University of North Carolina, Chapel Hill, NC 27599, USA
Brian White
Affiliation:
Department of Marine Sciences, University of North Carolina, Chapel Hill, NC 27599, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear instability mechanisms of horizontal convection in a rectangular cavity forced by a horizontal buoyancy gradient along its surface are investigated using local and global stability analyses for a Prandtl number equal to unity. The results show that the stability of the base flow, a steady circulation characterized by a narrow descending plume and a broad upwelling region, depends on the Rayleigh number, 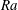$Ra$. For free-slip boundary conditions at a critical value of 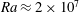$Ra\approx 2\times 10^{7}$, the steady base flow becomes unstable to three-dimensional perturbations, characterized by counter-rotating vortices originating within the plume region. A Wentzel–Kramers–Brillouin (WKB) method applied along closed streamlines demonstrates that this instability is of a Rayleigh–Taylor type and can be used to accurately reconstruct the global instability mode. In the case of no-slip boundary conditions, the base flow also becomes unstable to a self-sustained two-dimensional instability whose critical Rayleigh number is 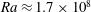$Ra\approx 1.7\times 10^{8}$. Beyond this critical 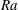$Ra$, two-dimensional equilibrium stationary states of the Navier–Stokes equations are computed using the selective frequency damping method. The two-dimensional onset of instability is shown to be characterized by a family of modes also originating within the plume. A local spatio-temporal stability analysis shows that the flow becomes absolutely unstable at the origin of the plume. Taken together, these results illustrate the mechanisms behind the onset of turbulence that has been observed in horizontal convection.

JFM classification

Convection: Buoyancy-driven instability Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 821 , 25 June 2017 , pp. 31 - 58
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.CrossRefGoogle Scholar
Bayly, B. J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31 (1), 56–64.Google Scholar
Beardsley, R. C. & Festa, J. F. 1972 A numerical model of convection driven by a surface stress and non-uniform horizontal heating. J. Phys. Oceanogr. 2, 444–455.Google Scholar
Chandler, G. J., Juniper, M. P., Nichols, J. W. & Schmid, P. J. 2012 Adjoint algorithms for the Navier–Stokes equations in the low Mach number limit. J. Comput. Phys. 231 (4), 1900–1916.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Chiu-webster, S., Hinch, E. J. & Lister, J. R. 2008 Very viscous horizontal convection. J. Fluid Mech. 611, 395–426.CrossRefGoogle Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Cunha, G., Passaggia, P.-Y. & Lazareff, M. 2015 Optimization of the selective frequency damping parameters using model reduction. Phys. Fluids 27 (9), 094103.CrossRefGoogle Scholar
Dolzhansky, F. V. 2012 Fundamentals of Geophysical Hydrodynamics. Springer.Google Scholar
Edwards, W. S., Tuckerman, L. S., Friesner, R. A. & Sorensen, D. C. 1994 Krylov methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 110 (1), 82–102.Google Scholar
Ehrenstein, U. & Gallaire, F. 2008 Two-dimensional global low-frequency oscillations in a separating boundary-layer flow. J. Fluid Mech. 614, 315–327.Google Scholar
Foures, D. P. G., Caulfield, C. P. & Schmid, P. J. 2014 Optimal mixing in two-dimensional plane poiseuille flow at finite Péclet number. J. Fluid Mech. 748, 241–277.Google Scholar
Gallaire, F., Marquillie, M. & Ehrenstein, U. 2007 Three-dimensional transverse instabilities in detached boundary layers. J. Fluid Mech. 571, 221–233.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Chomaz, J.-M. 2012 A relaxation method for large eigenvalue problems, with an application to flow stability analysis. J. Comput. Phys. 231 (10), 3912–3927.Google Scholar
Gayen, B., Griffiths, R. W. & Hughes, G. O. 2014 Stability transitions and turbulence in horizontal convection. J. Fluid Mech. 751, 698–724.Google Scholar
Gayen, B., Griffiths, R. W., Hughes, G. O. & Saenz, J. A. 2013 Energetics of horizontal convection. J. Fluid Mech. 716, R10.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Griffith, M. D., Thompson, M. C., Leweke, T., Hourigan, K. & Anderson, W. P. 2007 Wake behaviour and instability of flow through a partially blocked channel. J. Fluid Mech. 582, 319–340.Google Scholar
Griffiths, R. W., Hughes, G. O. & Gayen, B. 2013 Horizontal convection dynamics: insights from transient adjustment. J. Fluid Mech. 726, 559–595.Google Scholar
Hazewinkel, J., Paparella, F. & Young, W. R. 2012 Stressed horizontal convection. J. Fluid Mech. 692, 317–331.Google Scholar
Hill, D. C.1992 A theoretical approach for analyzing the restabilization of wakes. AIAA Paper 92–0067.Google Scholar
Houghton, J. T. 1977 The Physics of Atmospheres. Cambridge University Press.Google Scholar
Hunt, J. C. R. & Vassilicos, J. C. 2011 Turbulence Structure and Vortex Dynamics. Cambridge University Press.Google Scholar
Ilicak, M. & Vallis, G. 2012 Simulations and scaling of horizontal convection. Tellus A 64 (1), 18377.Google Scholar
Jeffreys, H. 1925 On fluid motions produced by differences of temperature and humidity. Q. J. R. Meteorol. Soc. 51, 347–356.Google Scholar
Juniper, M. P. & Pier, B. 2015 The structural sensitivity of open shear flows calculated with a local stability analysis. Eur. J. Mech. (B/Fluids) 49, 426–437.Google Scholar
Kaminski, A. K., Caulfield, C. P. & Taylor, J. R. 2014 Transient growth in strongly stratified shear layers. J. Fluid Mech. 758, R4.Google Scholar
Landman, M. J. & Saffman, P. G. 1987 The three-dimensional instability of strained vortices in a viscous fluid. Phys. Fluids 30 (8), 2339–2342.Google Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A 3 (11), 2644–2651.Google Scholar
Majda, A. J. & Shefter, M. G. 1998 Elementary stratified flows with instability at large Richardson number. J. Fluid Mech. 376, 319–350.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Marquillie, M. & Ehrenstein, U. 2002 Numerical simulation of separating boundary-layer flow. Comput. Fluids 31, 683–693.Google Scholar
Marquillie, M. & Ehrenstein, U. 2003 On the onset of nonlinear oscillations in a separating boundary-layer flow. J. Fluid Mech. 490, 169–188.Google Scholar
Mullarney, J. C., Griffiths, R. W. & Hughes, G. O. 2004 Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404 (6780), 837–840.Google Scholar
Paparella, F. & Young, W. R. 2002 Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214.CrossRefGoogle Scholar
Passaggia, P.-Y., Hurley, M. W., Scotti, A. & White, B.2017 Experiments on horizontal convection at high Rayleigh and Prandtl numbers. Phys. Rev. Fluids (accepted).CrossRefGoogle Scholar
Passaggia, P.-Y., Leweke, T. & Ehrenstein, U. 2012 Transverse instability and low-frequency flapping in incompressible separated boundary layer flows: an experimental study. J. Fluid Mech. 703, 363–373.Google Scholar
Passaggia, P.-Y., Meunier, P. & Le Dizès, S. 2014 Response of a stratified boundary layer on a tilted wall to surface undulations. J. Fluid Mech. 751, 663–684.Google Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.Google Scholar
Roche, P.-E., Castaing, B., Chabaud, B. & Hébral, B. 2002 Prandtl and Rayleigh numbers dependences in Rayleigh–Bénard convection. Europhys. Lett. 58 (5), 693–698.Google Scholar
Rossby, H. T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep-Sea Res. 12, 9–16.Google Scholar
Sandström, J. W. 1908 Dynamische versuche mit meerwasser. Ann. Hydrogr. Marit. Meteorol. 36, 6–23.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Scotti, A. 2008 A numerical study of the frontal region of gravity currents propagating on a free-slip boundary. Theor. Comput. Fluid Dyn. 22 (5), 383.Google Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really ‘non turbulent’? Geophys. Res. Lett. 38, L21609.Google Scholar
Scotti, A. & White, B. W. 2014 Diagnosing mixing in stratified turbulent flows with a locally defined available potential energy. J. Fluid Mech. 740, 114–135.Google Scholar
Sheard, G. J., Hussam, W. K. & Tsai, T. 2016 Linear stability and energetics of rotating radial horizontal convection. J. Fluid Mech. 795, 1–35.Google Scholar
Shishkina, O. & Wagner, S. 2016 Prandtl-number dependence of heat transport in laminar horizontal convection. Phys. Rev. Lett. 116 (2), 024302.Google Scholar
Sipp, D. & Jacquin, L. 1998 Elliptic instability in two-dimensional flattened Taylor–Green vortices. Phys. Fluids 10 (4), 839–849.Google Scholar
Sipp, D., Lauga, E. & Jacquin, L. 1999 Vortices in rotating systems: centrifugal, elliptic and hyperbolic type instabilities. Phys. Fluids 11 (12), 3716–3728.Google Scholar
Stern, M. 1975 Ocean Circulation Physics. Academic.Google Scholar
Stewart, K. D., Graham, H. O. & Griffiths, R. W. 2012 The role of turbulent mixing in an overturning circulation maintained by surface buoyancy forcing. J. Phys. Oceanogr. 42, 1907–1922.Google Scholar
Stewart, K. D., Hughes, O. & Griffiths, R. W. 2011 When do marginal seas and topographic sills modify the ocean density structure? J. Geophys. Res. 116, C08021.Google Scholar
Tailleux, R. & Rouleau, L. 2010 The effect of mechanical stirring on horizontal convection. Tellus A 62, 138–153.Google Scholar
Tsai, T., Hussam, W. K., Fouras, A. & Sheard, G. J. 2016 The origin of instability in enclosed horizontally driven convection. Intl J. Heat Mass Transfer 94, 509–515.Google Scholar
Whitehead, J. A. & Wang, W. 2008 Laboratory model of vertical ocean circulation driven by mixing. J. Phys. Oceanogr. 38, 1091–1106.Google Scholar