Published online by Cambridge University Press: 07 March 2012
We consider the classical problem of a single-layer homogeneous fluid at rest and a low, slowly varying, long and positive bottom obstacle, which is abruptly started from rest to move with a constant speed 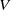 . As a result a system of transient waves will develop, and we assume that locally in the region over the obstacle dispersion can be ignored while nonlinearity cannot. The relevant governing equations for the near-field solution are therefore the nonlinear shallow water (NSW) equations. These are bidirectional and can be formulated in terms of a two-family system of characteristics. We analytically integrate and eliminate the backward-going family and achieve a versatile unidirectional single-family formulation, which covers subcritical, transcritical and supercritical conditions with relatively high accuracy. The formulation accounts for the temporal and spatial evolution of the bound waves in the vicinity of the obstacle as well as the development of the transient free waves generated at the onset of the motion. At some distance from the obstacle, dispersion starts to play a role and undular bores develop, but up to this point the new formulation agrees very well with numerical simulations based on a high-order Boussinesq formulation. Finally, we derive analytical asymptotic solutions to the new equations, providing estimates of the asymptotic surface levels in the vicinity of the obstacle as well as the crest levels of the leading non-dispersive free waves. These estimates can be used to predict the height and speed of the leading waves in the undular bores. The numerical and analytical solutions to the new single-family formulation of the NSW equations are compared to results based on the forced Korteweg–de Vries/Hopf equation and to numerical Boussinesq simulations.
. As a result a system of transient waves will develop, and we assume that locally in the region over the obstacle dispersion can be ignored while nonlinearity cannot. The relevant governing equations for the near-field solution are therefore the nonlinear shallow water (NSW) equations. These are bidirectional and can be formulated in terms of a two-family system of characteristics. We analytically integrate and eliminate the backward-going family and achieve a versatile unidirectional single-family formulation, which covers subcritical, transcritical and supercritical conditions with relatively high accuracy. The formulation accounts for the temporal and spatial evolution of the bound waves in the vicinity of the obstacle as well as the development of the transient free waves generated at the onset of the motion. At some distance from the obstacle, dispersion starts to play a role and undular bores develop, but up to this point the new formulation agrees very well with numerical simulations based on a high-order Boussinesq formulation. Finally, we derive analytical asymptotic solutions to the new equations, providing estimates of the asymptotic surface levels in the vicinity of the obstacle as well as the crest levels of the leading non-dispersive free waves. These estimates can be used to predict the height and speed of the leading waves in the undular bores. The numerical and analytical solutions to the new single-family formulation of the NSW equations are compared to results based on the forced Korteweg–de Vries/Hopf equation and to numerical Boussinesq simulations.