Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wen, Baole
Akhbari, Daria
Zhang, Li
and
Hesse, Marc A.
2018.
Convective carbon dioxide dissolution in a closed porous medium at low pressure.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
p.
56.
Sherman, Thomas
Paster, Amir
Porta, Giovanni
and
Bolster, Diogo
2019.
A spatial Markov model for upscaling transport of adsorbing-desorbing solutes.
Journal of Contaminant Hydrology,
Vol. 222,
Issue. ,
p.
31.
Zhang, Li
Hesse, Marc A.
and
Wang, Moran
2019.
Dispersion of charged solute in charged micro‐ and nanochannel with reversible sorption.
ELECTROPHORESIS,
Vol. 40,
Issue. 6,
p.
838.
Mederos, G.
Arcos, J.
Bautista, O.
and
Méndez, F.
2020.
Hydrodynamics rheological impact of an oscillatory electroosmotic flow on a mass transfer process in a microcapillary with a reversible wall reaction.
Physics of Fluids,
Vol. 32,
Issue. 12,
Sherman, Thomas
Bianchi Janetti, Emanuela
Guédon, Gaël Raymond
Porta, Giovanni
and
Bolster, Diogo
2020.
Upscaling transport of a sorbing solute in disordered non periodic porous domains.
Advances in Water Resources,
Vol. 139,
Issue. ,
p.
103574.
Venditti, Claudia
Giona, Massimiliano
and
Adrover, Alessandra
2022.
Exact moment analysis of transient/asymptotic dispersion properties in periodic media with adsorbing/desorbing walls.
Physics of Fluids,
Vol. 34,
Issue. 12,
Jiang, Weiquan
Zeng, Li
Fu, Xudong
and
Wu, Zi
2022.
Analytical solutions for reactive shear dispersion with boundary adsorption and desorption.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Huang, Po-Wei
Flemisch, Bernd
Qin, Chao-Zhong
Saar, Martin O.
and
Ebigbo, Anozie
2022.
Relating Darcy-Scale Chemical Reaction Order to Pore-Scale Spatial Heterogeneity.
Transport in Porous Media,
Vol. 144,
Issue. 2,
p.
507.
Lemoubou, Ernest Léontin
Kamdem, Hervé Thierry Tagne
Bogning, Jean Roger
Lazard, Myriam
and
Tonnang, Edouard Henri Zefack
2023.
Effects of heat and moisture transfer on the transient dynamic of solute transport in unsaturated soil under isothermal and thermal conditions.
Heat and Mass Transfer,
Vol. 59,
Issue. 5,
p.
919.
Lee, Woonghee
Yoon, Seonkyoo
and
Kang, Peter K.
2023.
Inertia and diffusion effects on reactive transport with fluid-solid reactions in rough fracture flows.
Physical Review Fluids,
Vol. 8,
Issue. 5,
Venditti, Claudia
Huygens, Bram
Desmet, Gert
and
Adrover, Alessandra
2023.
Moment analysis for predicting effective transport properties in hierarchical retentive porous media.
Journal of Chromatography A,
Vol. 1703,
Issue. ,
p.
464099.
Poddar, Nanda
Saha, Gourab
Mondal, Kajal Kumar
Dhar, Subham
and
Mazumder, B. S.
2024.
Effect of phase exchange kinetics on Taylor dispersion of chemically reactive solutes in an oscillatory magnetohydrodynamics flow between two parallel plates.
Physics of Fluids,
Vol. 36,
Issue. 5,
Aquino, Tomás
2024.
Equilibrium distributions under advection–diffusion in laminar channel flow with partially absorbing boundaries.
Journal of Fluid Mechanics,
Vol. 985,
Issue. ,
Saha, Gourab
Poddar, Nanda
Mondal, Kajal Kumar
and
Wang, Ping
2024.
Evolution of concentration distribution and removal of a solute in magnetohydrodynamics channel flow: effects of buoyancy-driven force and induced magnetic field.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 480,
Issue. 2300,
Das, Debabrata
Mondal, Kajal Kumar
Poddar, Nanda
and
Wang, Ping
2024.
Transient dispersion of a reactive solute in an oscillatory Couette flow through an anisotropic porous medium.
Physics of Fluids,
Vol. 36,
Issue. 2,
Zhan, Jie
Jiang, Weiquan
and
Wu, Zi
2024.
Reactive transport in open-channel flows with bed adsorption and desorption.
Journal of Hydrology,
Vol. 632,
Issue. ,
p.
130855.
Guan, Mingyang
and
Chen, Guoqian
2024.
Streamwise dispersion of soluble matter in solvent flowing through a tube.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
Woods, Andrew W.
2025.
Dispersive mixing: within or between pores?.
Journal of Fluid Mechanics,
Vol. 1006,
Issue. ,
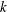 $k$ at late times. In the equilibrium sorption model, the time scale of the early regime and the duration of the transition to the late regime both increase with
$k$ at late times. In the equilibrium sorption model, the time scale of the early regime and the duration of the transition to the late regime both increase with 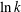 $\ln k$ for large
$\ln k$ for large 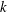 $k$. The early regime is pronounced in strongly sorbing systems (
$k$. The early regime is pronounced in strongly sorbing systems (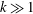 $k\gg 1$). The kinetic sorption model shows a similar transition from the early to the late transport regime and recovers the equilibrium results when adsorption and desorption rates are large. As the reaction rates slow down, the duration of the early regime increases, but the changes in transport velocity and dispersion relative to a tracer diminish. In general, if the partition coefficient
$k\gg 1$). The kinetic sorption model shows a similar transition from the early to the late transport regime and recovers the equilibrium results when adsorption and desorption rates are large. As the reaction rates slow down, the duration of the early regime increases, but the changes in transport velocity and dispersion relative to a tracer diminish. In general, if the partition coefficient 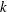 $k$ is large, the early regime is well developed and the behaviour is well characterized by the analysis of the limiting case without desorption.
$k$ is large, the early regime is well developed and the behaviour is well characterized by the analysis of the limiting case without desorption.


