Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-08T10:17:19.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient growth in strongly stratified shear layers

Published online by Cambridge University Press:  07 October 2014

A. K. Kaminski ,
C. P. Caulfield  and
J. R. Taylor
A. K. Kaminski
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK
J. R. Taylor*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

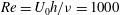We investigate numerically transient linear growth of three-dimensional perturbations in a stratified shear layer to determine which perturbations optimize the growth of the total kinetic and potential energy over a range of finite target time intervals. The stratified shear layer has an initial parallel hyperbolic tangent velocity distribution with Reynolds number $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}=U_0 h/\nu =1000$ and Prandtl number 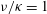$\nu /\kappa =1$, where $\nu $ is the kinematic viscosity of the fluid and $\kappa $ is the diffusivity of the density. The initial stable buoyancy distribution has constant buoyancy frequency 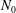$N_0$, and we consider a range of flows with different bulk Richardson number 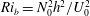${\mathit{Ri}}_b=N_0^2h^2/U_0^2$, which also corresponds to the minimum gradient Richardson number 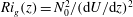${\mathit{Ri}}_g(z)=N_0^2/(\mathrm{d}U/\mathrm{d} z)^2$ at the midpoint of the shear layer. For short target times, the optimal perturbations are inherently three-dimensional, while for sufficiently long target times and small 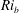${\mathit{Ri}}_b$ the optimal perturbations are closely related to the normal-mode ‘Kelvin–Helmholtz’ (KH) instability, consistent with analogous calculations in an unstratified mixing layer recently reported by Arratia et al. (J. Fluid Mech., vol. 717, 2013, pp. 90–133). However, we demonstrate that non-trivial transient growth occurs even when the Richardson number is sufficiently high to stabilize all normal-mode instabilities, with the optimal perturbation exciting internal waves at some distance from the midpoint of the shear layer.

JFM classification

Instability: Instability Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Stratified flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , R4
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, C., Caulfield, C. P. & Chomaz, J.-M. 2013 Transient perturbation growth in time-dependent mixing layers. J. Fluid Mech. 717, 90–133.CrossRefGoogle Scholar
Augier, P., Billant, P., Negretti, M. E. & Chomaz, J.-M. 2014 Experimental study of stratified turbulence forced with columnar dipoles. Phys. Fluids 26 (4), 046603.CrossRefGoogle Scholar
Bretherton, F. P. & Garrett, C. J. R. 1969 Wavetrains in inhomogeneous moving media. Proc. R. Soc. Lond. A 302, 529–554.Google Scholar
Constantinou, N. C. & Ioannou, P. J. 2011 Optimal excitation of two-dimensional Holmboe instabilities. Phys. Fluids 23, 074102.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn Cambridge University Press.CrossRefGoogle Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18 (4), 487–488.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1993a Optimal excitation of three-dimensional perturbations in viscous constant shear flow. Phys. Fluids A 5 (6), 1390–1400.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1993b Transient development of perturbations in stratified shear flow. J. Atmos. Sci. 50 (14), 2201–2214.2.0.CO;2>CrossRefGoogle Scholar
Foures, D. P. G., Caulfield, C. P. & Schmid, P. J. 2012 Variational framework for flow optimization using seminorm constraints. Phys. Rev. E 86, 026306.CrossRefGoogle ScholarPubMed
Garrett, C. 2003 Mixing with latitude. Nature 422, 477–478.CrossRefGoogle ScholarPubMed
Holmboe, J. 1962 On the behaviour of symmetric waves in stratified shear layers. Geophys. Publ. 24, 67–113.Google Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimization approach for analyzing nonlinear stability with transition to turbulence in fluids as an exemplar. Rep. Prog. Phys. 77, 085901.CrossRefGoogle Scholar
Kuhlbrodt, T., Griesel, A., Montoya, M., Levermann, A., Hofmann, M. & Rahmstorf, S. 2007 On the driving processes of the Atlantic meridional overturning circulation. Rev. Geophys. 45, RG2001.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98 (2), 243–251.CrossRefGoogle Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.CrossRefGoogle Scholar
Mack, S. A. & Schoeberlein, H. C. 2004 Richardson number and ocean mixing: towed chain observations. J. Phys. Oceanogr. 34 (4), 736–754.2.0.CO;2>CrossRefGoogle Scholar
Orr, W. M. F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I: a perfect liquid. Proc. R. Irish Acad. A 27, 9–68.Google Scholar
Polzin, K. & Ferrari, R. 2004 Isopycnal dispersion in NATRE. J. Phys. Oceanogr. 34 (1), 247–257.2.0.CO;2>CrossRefGoogle Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2012 Triggering turbulence efficiently in plane Couette flow. J. Fluid Mech. 712, 244–272.CrossRefGoogle Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.CrossRefGoogle Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer. PhD thesis, University of California, San Diego.Google Scholar
Tearle, M. O.2004 Optimal perturbation analysis of stratified shear flow. PhD thesis, University of Colorado.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.CrossRefGoogle Scholar