Published online by Cambridge University Press: 01 November 2013
Characterizing scalar dispersion is a key concern in a wide variety of applications, including both steady-state and time-dependent studies of wastewater outfalls, salinity distribution in estuaries, and the spreading of pollutants from industrial spills. As the size of a scalar plume grows with respect to the size of the containing water body, the effective dispersion varies, from the well-known 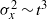 ${ \sigma }_{x}^{2} \sim {t}^{3} $ behaviour for a plume enveloped in a region of linear shear, to the
${ \sigma }_{x}^{2} \sim {t}^{3} $ behaviour for a plume enveloped in a region of linear shear, to the 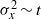 ${ \sigma }_{x}^{2} \sim t$ behaviour at the limit of a laterally well-mixed plume. We introduce an additional regime in which the plume extends across the full range of the available shear, but is not significantly affected by the lateral bounds of the water body. Through an analytic treatment we show that this regime exhibits a
${ \sigma }_{x}^{2} \sim t$ behaviour at the limit of a laterally well-mixed plume. We introduce an additional regime in which the plume extends across the full range of the available shear, but is not significantly affected by the lateral bounds of the water body. Through an analytic treatment we show that this regime exhibits a 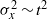 ${ \sigma }_{x}^{2} \sim {t}^{2} $ behaviour, independent of lateral mixing coefficient. Particle tracking results in an idealized, tidal channel–shoal basin demonstrate this regime as particle clouds straddle the channel–shoal interface. Quantitative analysis of spatial moments as plumes transition between regimes show good correlation between the observed parameters and parameters predicted by the analytic framework.
${ \sigma }_{x}^{2} \sim {t}^{2} $ behaviour, independent of lateral mixing coefficient. Particle tracking results in an idealized, tidal channel–shoal basin demonstrate this regime as particle clouds straddle the channel–shoal interface. Quantitative analysis of spatial moments as plumes transition between regimes show good correlation between the observed parameters and parameters predicted by the analytic framework.