Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-06T08:00:29.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Tracking of vortices in a turbulent boundary layer

Published online by Cambridge University Press:  06 March 2012

G. E. Elsinga ,
C. Poelma ,
A. Schröder ,
R. Geisler ,
F. Scarano  and
J. Westerweel
G. E. Elsinga*
Affiliation:
Laboratory for Aero & Hydrodynamics, Department of Mechanical Engineering, Delft University of Technology, Leeghwaterstraat 21, 2628CA Delft, The Netherlands
C. Poelma
Affiliation:
Laboratory for Aero & Hydrodynamics, Department of Mechanical Engineering, Delft University of Technology, Leeghwaterstraat 21, 2628CA Delft, The Netherlands
A. Schröder
Affiliation:
Deutsches Zentrum für Luft- und Raumfahrt, Institut für Aerodynamik und Strömungstechnik, Bunsenstrasse 10, 37073 Göttingen, Germany
R. Geisler
Affiliation:
Deutsches Zentrum für Luft- und Raumfahrt, Institut für Aerodynamik und Strömungstechnik, Bunsenstrasse 10, 37073 Göttingen, Germany
F. Scarano
Affiliation:
Department of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629HS Delft, The Netherlands
J. Westerweel
Affiliation:
Laboratory for Aero & Hydrodynamics, Department of Mechanical Engineering, Delft University of Technology, Leeghwaterstraat 21, 2628CA Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The motion of spanwise vortical elements and large-scale bulges has been tracked in the outer region between wall-normal distance 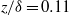and 0.30 of a turbulent boundary layer at 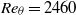. The experimental dataset of time-resolved three-dimensional velocity fields used has been obtained by tomographic particle image velocimetry. The tracking of these structures yields their respective average trajectories as well as the variations thereof, quantified by the root mean square of the trajectory coordinates as a function of time. It is demonstrated that the variation in convection can be described by a dispersion model for infinitesimal particles in homogeneous turbulence, which suggests that these vortical structures and bulges are transported passively by the external velocity field without significant changes in their topology, at least over the present observation time of 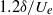. However, this does not mean that the structure’s convection velocity is equal to the local flow velocity at each instant. Differences of the order of the Kolmogorov or wall friction velocity have been observed for the spanwise vortical elements. In addition, the simultaneous detection and tracking of multiple structures allows an evaluation of the relative velocity between two spanwise vortex elements, which are approximately aligned along the streamwise direction. The typical streamwise distance between such neighbouring structures is found to be around 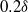. Their relative velocities are small, especially the streamwise component, which shows less variation as may be expected based on the relative flow velocity statistics for the same separation distance. This appears consistent with the hairpin packet model, which comprises a set of streamwise aligned hairpins travelling coherently. In exceptional cases, however, the structures approach each other rapidly, forcing an interaction on a time scale of the order of . It is shown that the measured variation in convection velocity can further be used successfully to predict the temporal development of space–time correlation functions starting from the instantaneous correlation map. In this prediction the structures are assumed to convect without change, following our observations.

JFM classification

Boundary Layers: Boundary Layers Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 697 , 25 April 2012 , pp. 273 - 295
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
2. Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
3. Del Alamo, J. C. & Jimenez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
4. Balakumar, B. J. & Adrian, R. J. 2007 Large- and very large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
5. Bradshaw, P. 1967 Inactive motion and pressure fluctuation in turbulent boundary layer. J. Fluid Mech. 30, 241–258.CrossRefGoogle Scholar
6. Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
7. Dennis, D. J. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.CrossRefGoogle Scholar
8. Dennis, D. J. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.CrossRefGoogle Scholar
9. Elsinga, G. E., Adrian, R. J., van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.CrossRefGoogle Scholar
10. Elsinga, G. E. & Marusic, I. 2010 Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22, 015102.CrossRefGoogle Scholar
11. Elsinga, G. E., Scarano, F., Wieneke, B. & Van Oudheusden, B. W. 2006 Tomographic particle image velocimetry. Exp. Fluids 41, 933–947.CrossRefGoogle Scholar
12. Falco, R. E. 1977 Coherent motions in the outer region of turbulent boundary layers. Phys. Fluids 20, S124–S132.CrossRefGoogle Scholar
13. Ferre, J. A. & Giralt, F. 1989 Pattern-recognition analysis of the velocity field in plane turbulent wakes. J. Fluid Mech. 198, 27–64.CrossRefGoogle Scholar
14. Guezennec, Y. G., Piomelli, U. & Kim, J. 1989 On the shape and dynamics of wall structures in turbulent channel flow. Phys. Fluids A 1, 764–766.CrossRefGoogle Scholar
15. Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106, 134503.CrossRefGoogle ScholarPubMed
16. Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
17. Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.CrossRefGoogle Scholar
18. Kim, J. & Hussain, F. 1993 Propagation velocity of pertubations in turbulent channel flow. Phys. Fluids A 3, 695–706.CrossRefGoogle Scholar
19. Krogstad, P. A., Kaspersen, J. H. & Rimestad, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10, 949–957.CrossRefGoogle Scholar
20. Lüthi, B., Tsinober, A. & Kinzelbach, W. 2005 Lagrangian measurements of vorticity dynamics in turbulent flow. J. Fluid Mech. 528, 87–118.CrossRefGoogle Scholar
21. Moin, P. 2009 Revisiting Taylor’s hypothesis. J. Fluid Mech. 640, 1–4.CrossRefGoogle Scholar
22. Pirozzoli, S., Bernardini, M. & Grasso, F. 2008 Characterization of coherent vortical structures in a supersonic turbulent boundary layer. J. Fluid Mech. 613, 205–231.CrossRefGoogle Scholar
23. Scarano, F., Benocci, C. & Riethmuller, M. L. 1999 Pattern recognition analysis of the turbulent flow past a backward facing step. Phys. Fluids 11, 3808–3818.CrossRefGoogle Scholar
24. Schröder, A., Geisler, R., Elsinga, G. E., Scarano, F. & Dierksheide, U. 2008 Investigation of a turbulent spot and a tripped turbulent boundary flow using time-resolved tomographic PIV. Exp. Fluids 44, 305–316.CrossRefGoogle Scholar
25. Schröder, A., Geisler, R., Staack, K., Elsinga, G. E., Scarano, F., Wieneke, B., Henning, A., Poelma, C. & Westerweel, J. 2011 Eulerian and Lagrangian views of a turbulent boundary layer flow using time-resolved tomographic PIV. Exp. Fluids 50, 1071–1091.CrossRefGoogle Scholar
26. Taylor, G. I. 1921 Diffusion by continous movements. Proc. Lond. Math. Soc. 20, 196–202.Google Scholar
27. Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. 164, 476–490.Google Scholar
28. Tennekes, H. 1979 The exponential Lagrangian correlation function and turbulent diffusion in the inertial subrange. Atmos. Environ. 13, 1565–1567.CrossRefGoogle Scholar
29. Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
30. Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar
31. Willmarth, W. W. & Wooldridge, C. E. 1962 Measurements of the fluctuating pressure at the wall beneath a thick turbulent boundary layer. J. Fluid Mech. 14, 187–210.CrossRefGoogle Scholar
32. Wills, J. A. B. 1964 On convection velocities in turbulent shear flows. J. Fluid Mech. 20, 417–432.CrossRefGoogle Scholar
33. Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.CrossRefGoogle Scholar