Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T13:21:07.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Topology of vortex breakdown in closed polygonal containers

Published online by Cambridge University Press:  05 May 2017

Igor V. Naumov Open the ORCID record for Igor V. Naumov [Opens in a new window]  and
Irina Yu. Podolskaya
Igor V. Naumov*
Affiliation:
Kutateladze Institute of Thermophysics SB RAS 630090, Novosibirsk, Russia
Irina Yu. Podolskaya
Affiliation:
Kutateladze Institute of Thermophysics SB RAS 630090, Novosibirsk, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The topology of vortex breakdown in the confined flow generated by a rotating lid in a closed container with a polygonal cross-section geometry has been analysed experimentally and numerically for different height/radius aspect ratios 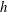$h$ from 0.5 to 3.0. The locations of stagnation points of the breakdown bubble emergence and corresponding Reynolds numbers were determined experimentally and numerically by STAR-CCM+ computational fluid dynamics software for square, pentagonal, hexagonal and octagonal cross-section configurations. The flow pattern and velocity were observed and measured by combining seeding particle visualization and laser Doppler anemometry. The vortex breakdown size and position on the container axis were identified for Reynolds numbers ranging from 500 to 2800 in steady flow conditions. The obtained results were compared with the flow structure in the closed cylindrical container. The results allowed revealing regularities of formation of the vortex breakdown bubble depending on 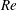$Re$ and 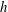$h$ and the cross-section geometry of the confined container. It was found in a diagram of 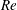$Re$ versus 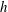$h$ that reducing the number of cross-section angles from eight to four shifts the breakdown bubble location to higher Reynolds numbers and a smaller aspect ratio. The vortex breakdown bubble area for octagonal cross-section was detected to correspond to the one for the cylindrical container but these areas for square and cylindrical containers do not overlap in the entire range of aspect ratio.

JFM classification

Flow Control: Flow Control Vortex Flows: Vortex breakdown Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 263 - 283
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brøns, M., Shen, V. Z. & Sørensen, J. N. 2007 The influence of imperfections on the flow structure of steady vortex breakdown bubbles. J. Fluid Mech. 578, 453–466.Google Scholar
Brøns, M., Voigt, L. K. & Sørensen, J. N. 1999 Streamline topology of steady axisymmetric vortex breakdown in a cylinder with co- and counter-rotating end-cover. J. Fluid Mech. 401, 275–292.Google Scholar
Dubnishev, Y. N., Meledin, V. G., Pavlov, V. A. & Yavorskiy, N. I. 2003 The flow structure and energy separation investigation in the vortex tube with square section. Thermophys. Aeromech. 10, 587–598.Google Scholar
Dusting, J., Sheridan, J. & Hourigan, K. 2006 A fluid dynamics approach to bioreactor design for cell and tissue culture. Biotechnol. Bioengng 94, 1196–1208.Google Scholar
Escudier, M. P. 1984 Observations of the flow produced in a cylindrical container by a rotating endwall. Exp. Fluids 2, 189–196.Google Scholar
Faler, J. H. & Leibovich, S. 1978 An experimental map of the internal structure of a vortex breakdown. J. Fluid Mech. 86, 313–335.Google Scholar
Gelfgat, A. Y., Bar-Yoseph, P. Z. & Solan, A. 2001 Three-dimensional instability of axisymmetric flow in rotating lid-cylinder enclosure. J. Fluid Mech. 438, 363–377.CrossRefGoogle Scholar
Herrada, M. A., Shtern, V. N. & Torregrosa, M. M. 2015 The instability nature of the Vogel–Escudier flow. J. Fluid Mech. 766, 590–610.Google Scholar
Lopez, J. M. 1990 Axisymmetric vortex breakdown. Part 1: confined swirling flow. J. Fluid Mech. 221, 533–552.Google Scholar
Lopez, J. M. 2012 Three-dimensional swirling flows in a tall cylinder driven by a rotating endwall. Phys. Fluids 24, 014101.Google Scholar
Mununga, L., Lo Jacono, D., Sørensen, J. N., Leweke, T., Thompson, M.C. & Hourigan, K. 2014 Control of confined vortex breakdown with partial rotating lids. J. Fluid Mech. 738, 5–33.Google Scholar
Naumov, I. V., Dvoynishnikov, S. V., Kabardin, I. K. & Tsoy, M. A. 2015 Vortex breakdown in closed containers with polygonal cross sectionl. Phys. Fluids 27, 124103.Google Scholar
Naumov, I. V., Mikkelsen, R. F. & Okulov, V. L. 2014 Stagnation zone formation on the axis of a closed vortex flow. Thermophys. Aeromech. 21, 767–770.Google Scholar
Okulov, V. L., Meledin, V. G. & Naumov, I. V. 2003 Experimental investigation of a swirling flow in a cubic container. Tech. Phys. 48, 1249–1254.Google Scholar
Shtern, V. N. 2012 Counterflows, Cambridge University Press.CrossRefGoogle Scholar
Shtern, V. N., Torregrosa, M. M. & Herrada, M. A. 2012 Effect of swirl decay on vortex breakdown in a confined steady axisymmetric flow. Phys. Fluids 24, 043601.CrossRefGoogle Scholar
Sørensen, J. N., Gelfgat, A. Y., Naumov, I. V. & Mikkelsen, R. 2009 Experimental and numerical results on the three-dimensional instabilities in a rotating disk-tall cylinder flow. Phys. Fluids 21, 054102.Google Scholar
Sørensen, J. N., Naumov, I. & Mikkelsen, R. 2006 Experimental investigation in three-dimensional flow instabilities in a rotating lid-driven cavity. Exp. Fluids 41, 425–440.CrossRefGoogle Scholar
Sørensen, J. N., Naumov, I. V. & Okulov, V. L. 2011 Multiple helical modes of vortex breakdown. J. Fluid Mech. 683, 430–441.Google Scholar
Thompson, M. C. & Hourigan, K. 2003 The sensitivity of steady vortex breakdown bubbles in confined cylinder flows to rotating lid misalignment. J. Fluid Mech. 496, 129–138.CrossRefGoogle Scholar
Yu, P., Lee, T. S., Zeng, Y. & Low, H. T. 2006 Effects of conical lids on vortex breakdown in an enclosed cylindrical chamber. Phys. Fluids 18, 117101.Google Scholar
Yu, P., Lee, T. S., Zeng, Y. & Low, H. T. 2007 Characterization of flow behavior in an enclosed cylinder with a partially rotating end wall. Phys. Fluids 19, 057104.Google Scholar
Yu, P., Lee, T. S., Zeng, Y. & Low, H. T. 2008 Steady axisymmetric flow in n enclosed conical frustrum chamber with a rotating bottom wall. Phys. Fluids 20, 087103.Google Scholar
Yu, P. & Meguid, S. A. 2009 Effects of wave sidewall on vortex breakdown in an enclosed cylindrical chamber with a rotating end wall. Phys. Fluids 21, 017104.Google Scholar
Zykova, N. G., Serant, F. A., Nozdrenko, G. V. & Shchinnikov, P. A. 2003 Scheme and parameter optimization of tep boilers with an annular furnace. Thermophys. Aeromech. 10, 465–473.Google Scholar