Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T01:49:34.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological bifurcations of vortex pair interactions

Published online by Cambridge University Press:  23 April 2021

Anne R. Nielsen Open the ORCID record for Anne R. Nielsen [Opens in a new window] ,
Morten Andersen Open the ORCID record for Morten Andersen [Opens in a new window] ,
Jesper S. Hansen  and
Morten Brøns Open the ORCID record for Morten Brøns [Opens in a new window]
Anne R. Nielsen*
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800Lyngby, Denmark
Morten Andersen
Affiliation:
Department of Science and Environment, Roskilde University, 4000Roskilde, Denmark
Jesper S. Hansen
Affiliation:
Department of Science and Environment, Roskilde University, 4000Roskilde, Denmark
Morten Brøns
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800Lyngby, Denmark
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

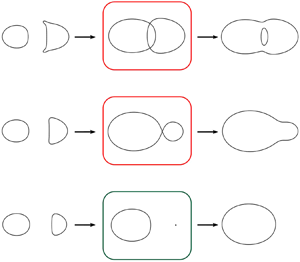
We investigate vortex pair interactions at low Reynolds numbers. We base our analysis on the Q-criterion, where a vortex is defined as a region where the local rotation dominates the strain, and we make use of a topological approach to describe the qualitative changes of the vortex structure. In order to give a complete description of vortex pair interactions we further develop a general bifurcation theory for $Q$-vortices and prove that a threshold for vortex merging may occur when we allow two parameters to vary. To limit the number of free parameters, we study the interactions with two point vortices as the initial condition and show that the threshold is a codimension two bifurcation that appears as a cusp singularity on a bifurcation curve. We apply the general theory to the analytically tractable core growth model and conclude that a pair of co-rotating vortices merge only if their strength ratio, $\alpha =\varGamma _1/\varGamma _2$ is less than $4.58$. Below this threshold value, we observe two different regimes in which the merging processes can be described with different sequences of bifurcations. By comparison with Navier–Stokes simulations at different Reynolds numbers, we conclude that the merging threshold varies only slightly for Reynolds numbers up to $100$. Furthermore, we observe an excellent agreement between the core growth model and the numerical simulations for Reynolds numbers below 10. We therefore conclude that, instead of solving the Navier–Stokes equation numerically we can, for sufficiently small Reynolds numbers, apply the core growth model as a simple, analytically tractable model with a low dimension.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Vortex Flows: Vortex interactions Mathematical Foundations: Topological fluid dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 917 , 25 June 2021 , A11
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andersen, M., Schreck, C., Hansen, J.S. & Brøns, M. 2019 Vorticity topology of vortex pair interactions at low Reynolds numbers. Eur. J. Mech. B/Fluids 74, 58–67.CrossRefGoogle Scholar
Brandt, L.K. & Nomura, K.K. 2010 Characterization of the interactions of two unequal co-rotating vortices. J. Fluid Mech. 646, 233–253.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R.J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Chen, Q., Zhong, Q., Qi, M. & Wang, X. 2015 Comparison of vortex identification criteria for planar velocity fields in wall turbulence. Phys. Fluids 27 (8), 085101.CrossRefGoogle Scholar
Deem, G.S. & Zabusky, N.J. 1978 Vortex waves – stationary $V$ states, interactions, recurrence, and breaking. Phys. Rev. Lett. 40 (13), 859–862.CrossRefGoogle Scholar
Dritschel, D.G. 1985 The stability and energetics of corotating uniform vortices. J. Fluid Mech. 157, 95–134.CrossRefGoogle Scholar
Dritschel, D.G. 1986 Contour surgery: a topological reconnection scheme for extended integrations using contour dynamics. J. Comput. Phys. 77 (77), 240–266.CrossRefGoogle Scholar
Dritschel, D.G. 1995 A general theory for two-dimensional vortex interactions. J. Fluid Mech. 293, 269–303.CrossRefGoogle Scholar
Dritschel, D.G. & Waugh, D.W. 1992 Quantification of the inelastic interaction of unequal vortices in 2-dimensional vortex dynamics. Phys. Fluids A 4 (8), 1737–1744.CrossRefGoogle Scholar
Elsas, J.H. & Moriconi, L. 2017 Vortex identification from local properties of the vorticity field. Phys. Fluids 29 (1), 015101.CrossRefGoogle Scholar
Folz, P.J.R. & Nomura, K.K. 2017 A quantitative assessment of viscous asymmetric vortex pair interactions. J. Fluid Mech. 829, 1–30.CrossRefGoogle Scholar
Gallay, T. 2011 Interaction of vortices in weakly viscous planar flows. Arch. Rat. Mech. Anal. 200 (2), 445–490.CrossRefGoogle Scholar
Gallay, T. & Wayne, C.E. 2005 Global stability of vortex solutions of the two-dimensional Navier–Stokes equation. Commun. Math. Phys. 255 (1), 97–129.CrossRefGoogle Scholar
Hansen, J.S. 2011 GNU Octave – Beginner's Guide. Packt Publishing.Google Scholar
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research, Stanford University.Google Scholar
Jalali, M.M. & Dritschel, D.G. 2018 The interaction of two asymmetric quasi-geostrophic vortex patches. Geophys. Astrophys. Fluid Dyn. 112 (6), 375–401.CrossRefGoogle Scholar
Jalali, M.M. & Dritschel, D.G. 2020 Stability and evolution of two opposite-signed quasi-geostrophic shallow-water vortex patches. Geophys. Astrophys. Fluid Dyn. 114 (4–5), 561–587.CrossRefGoogle Scholar
Jing, F., Kanso, E. & Newton, P.K. 2010 Viscous evolution of point vortex equilibria: the collinear state. Phys. Fluids 22 (12), 123102.CrossRefGoogle Scholar
Jing, F., Kanso, E. & Newton, P.K. 2012 Insights into symmetric and asymmetric vortex mergers using the core growth model. Phys. Fluids 24 (7), 073101.CrossRefGoogle Scholar
Kim, S.C. & Sohn, S.I. 2012 Interactions of three viscous point vortices. J. Phys. A: Math. Theor. 45 (45), 455501.CrossRefGoogle Scholar
Leweke, T., Le Dizès, S. & Williamson, C.H.K. 2016 Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 48 (1), 507–541.CrossRefGoogle Scholar
Melander, M.V., Zabusky, N.J. & McWilliams, J.C. 1988 Symmetric vortex merger in two dimensions: causes and conditions. J. Fluid Mech. 195, 303–340.CrossRefGoogle Scholar
Meunier, P., Ehrenstein, U., Leweke, T. & Rossi, M. 2002 A merging criterion for two-dimensional co-rotating vortices. Phys. Fluids 14 (8), 2757–2766.CrossRefGoogle Scholar
Nielsen, A.R., Heil, M., Andersen, M. & Brøns, M. 2019 Bifurcation theory for vortices with application to boundary layer eruption. J. Fluid Mech. 865, 831–849.CrossRefGoogle Scholar
Overman, E.A. & Zabusky, N.J. 1982 Evolution and merger of isolated vortex structures. Phys. Fluids 25 (8), 1297–1305.CrossRefGoogle Scholar
Rutter, J.W. 2000 Geometry of Curves. Taylor & Francis.Google Scholar
Saffman, P.G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Trieling, R.R., Velasco Fuentes, O.U. & van Heijst, G.J.F. 2005 Interaction of two unequal corotating vortices. Phys. Fluids 17 (8), 087103.CrossRefGoogle Scholar
Weinan, E. & Liu, J.-G. 1996 a Finite difference schemes for incompressible flows in vorticity formulations. ESIAM: Proc. 1, 181–195.Google Scholar
Weinan, E. & Liu, J.-G. 1996 b Vorticity boundary conditions and related issues for finite difference schemes. J. Comput. Phys. 124, 368–382.Google Scholar
Zhang, Y., Liu, K., Xian, H. & Du, X. 2018 A review of methods for vortex identification in hydroturbines. Renew. Sust. Energ. Rev. 81, 1269–1285.CrossRefGoogle Scholar