Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T10:19:09.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Tomographic PIV investigation on 3D wake structures for flow over a wall-mounted short cylinder

Published online by Cambridge University Press:  17 October 2017

Hang-Yu Zhu ,
Cheng-Yue Wang ,
Hong-Ping Wang  and
Jin-Jun Wang Open the ORCID record for Jin-Jun Wang [Opens in a new window]
Hang-Yu Zhu
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Cheng-Yue Wang
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Hong-Ping Wang
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Jin-Jun Wang*
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Tomographic particle image velocimetry (TPIV) measurement with six high-resolution charge-coupled device (CCD) cameras is conducted to investigate flow structures over a finite circular cylinder with an aspect ratio of 2 (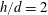$h/d=2$). This short wall-mounted cylinder is fully immersed in a thick turbulent boundary layer (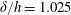$\unicode[STIX]{x1D6FF}/h=1.025$). Focus is placed on the three-dimensional instantaneous vortex structures and their dynamic characteristics in the wake flow fields. Based on the present results, a refined topological model of the mean wake field behind the finite circular cylinder is proposed, where the spatial locations of the typical vortex structures and their interactions are described in more detail. Among the reported typical vortex structures (i.e. the horseshoe, tip, base, trailing and arch vortex), emphasis is laid on discussion of the tip and arch vortex. The instantaneous 3D M-shape arch vortex and an alternating large-scale streamwise vortex are first found in the present experiment, and their developments are also discussed. Therefore, it is suggested that the instantaneous finite-cylinder wake is dominated by the arch vortex system and the large-scale streamwise vortices. Moreover, in the instantaneous volumetric flow fields, both the antisymmetric and the symmetric wake behaviours are observed. With proper orthogonal decomposition (POD) analysis, the dynamic characteristics of the wake field are clarified. Different from the flow around an infinite cylinder without control, the third and fourth POD modes are characterized by low-frequency symmetric shedding. The low-frequency feature shown in the second mode pair is observed and associated with the occurrence of instantaneous symmetric 3D wake behaviour triggered by the low-aspect-ratio effect and the extension of the separated shear layer. The low frequency seems be attributed to the flapping phenomenon, i.e. oscillation of the recirculation in the backward-facing step flow. It is found that the flapping motion has a modulating effect on the occurrence of the antisymmetric shedding vortex and thus the large-scale streamwise vortex.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 743 - 778
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adaramola, M. S., Akinlade, O. G., Sumner, D., Bergstrom, D. J. & Schenstead, A. J. 2006 Turbulent wake of a finite circular cylinder of small aspect ratio. J. Fluid Struct. 22, 919–928.Google Scholar
Bourgeois, J. A., Noack, B. R. & Martinuzzi, R. J. 2013 Generalized phase average with applications to sensor-based flow estimation of the wall-mounted square cylinder wake. J. Fluid Mech. 736, 316–350.Google Scholar
Bourgeois, J. A., Sattari, P. & Martinuzzi, R. J. 2011 Alternating half-loop shedding in the turbulent wake of a finite surface-mounted square cylinder with a thin boundary layer. Phys. Fluids 23, 095101.Google Scholar
Chatterjee, A. 2000 An introduction to the proper orthogonal decomposition. Curr. Sci. 78, 171–174.Google Scholar
Eaton, J. K. & Johnston, J.1980 Turbulent flow reattachment: an experimental study of the flow and structure behind a backward-facing step. Tech. Rep. MD-39. Thermosciences Division, Department of Mechanical Engineering, Stanford University.Google Scholar
Elsinga, G. E., Scarano, F., Wieneke, B. & van Oudheusden, B. W. 2006 Tomographic particle image velocimetry. Exp. Fluids 41, 933–947.Google Scholar
Etzold, F. & Fiedler, H. 1976 The near-wake structure of a cantilevered cylinder in a cross-flow. Z. Flugwiss. 24, 77–82.Google Scholar
Feng, L. H., Wang, J. J. & Pan, C. 2011 Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control. Phys. Fluids 23 (1), 014106.Google Scholar
Frederich, O., Wassen, E., Thiele, F., Jensch, M., Brede, M., Hüttmann, F. & Leder, A. 2008 Numerical simulation of the flow around a finite cylinder with ground plate in comparison to experimental measurements. In New Results in Numerical and Experimental Fluid Mechanics VI (ed. Tropea, C., Jakirlic, S., Heinemann, H.-J., Henke, R. & Hönlinger, H.), pp. 348–355. Springer.Google Scholar
Friedrich, R. & Arnal, M. 1990 Analysing turbulent backward-facing step flow with the lowpass-filtered Navier–Stokes equations. J. Wind Engng Ind. Aerodyn. 35, 101–128.Google Scholar
Fröhlich, J. & Rodi, W. 2004 LES of the flow around a circular cylinder of finite height. Intl J. Heat Fluid Flow 25, 537–548.Google Scholar
Haimes, R. & Kenwright, D. 1999 On the velocity gradient tensor and fluid feature extraction. In 14th AIAA Computational Fluid Dynamics Conference, June, 1999, Norfolk, VA, USA, American Institute of Aeronautics and Astronautics.Google Scholar
Hain, R., Kähler, C. J. & Michaelis, D. 2008 Tomographic and time resolved PIV measurements on a finite cylinder mounted on a flat plate. Exp. Fluids 45, 715–724.Google Scholar
Hassan, M. E., Bourgeois, J. & Martinuzzi, R. 2015 Boundary layer effect on the vortex shedding of wall-mounted rectangular cylinder. Exp. Fluids 56, 1–19.Google Scholar
He, G.-S., Pan, C., Feng, L.-H., Gao, Q. & Wang, J.-J. 2016 Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer. J. Fluid Mech. 792, 274–306.Google Scholar
Hosseini, Z., Bourgeois, J. A. & Martinuzzi, R. J. 2013 Large-scale structures in dipole and quadrupole wakes of a wall-mounted finite rectangular cylinder. Exp. Fluids 54, 1–16.Google Scholar
Hunt, J. C., Wray, A. A. & Moin, P.1988 Eddies, streams, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research.Google Scholar
Kawamura, T., Hiwada, M., Hibino, T., Mabuchi, I. & Kumada, M. 1984 Flow around a finite circular cylinder on a flat plate (cylinder height greater than turbulent boundary layer thickness). Bull. JSME 27, 2142–2151.Google Scholar
Krajnović, S. 2011 Flow around a tall finite cylinder explored by large eddy simulation. J. Fluid Mech. 676, 294–317.Google Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.Google Scholar
Leder, A. 2003 3D-flow structures behind truncated circular cylinders. In Proceedings of the Fluids Engineering Division Summer Meeting (FEDSM 2003) at 4th ASME/JSME Joint Fluids Summer Engineering Conference 6–10 July, 2003, Honolulu, Hawaii, American Society of Mechanical Engineers.Google Scholar
Lee, L. W. 1997 Wake structure behind a circular cylinder with a free end. Proc. Heat Transfer Fluid Mech. Inst. 35, 241–251.Google Scholar
Ma, L. Q., Feng, L. H., Pan, C., Gao, Q. & Wang, J. J. 2015 Fourier mode decomposition of PIV data. Sci. China Technol. Sc. 58, 1935–1948.Google Scholar
Moazamigoodarzi, N., Bergstrom, D., Einian, M. & Sumner, D. 2014 Phase average visualization of a finite cylinder wake as predicted by large eddy simulation. In Fluid-Structure-Sound Interactions and Control, pp. 71–76. Springer.CrossRefGoogle Scholar
Noack, B. R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.Google Scholar
van Oudheusden, B. W., Scarano, F., Hinsberg, N. P. & Watt, D. W. 2005 Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 39, 86–98.Google Scholar
Palau-Salvador, G., Stoesser, T., Fröhlich, J., Kappler, M. & Rodi, W. 2010 Large eddy simulations and experiments of flow around finite-height cylinders. Flow Turbul. Combust. 84, 239–275.Google Scholar
Park, C. W. & Lee, S. J. 2002 Flow structure around a finite circular cylinder embedded in various atmospheric boundary layers. Fluid Dyn. Res. 30, 197–215.Google Scholar
Pattenden, R. J., Turnock, S. R. & Zhang, X. 2005 Measurements of the flow over a low-aspect. Exp. Fluids 39, 10–21.Google Scholar
Porteous, R., Moreau, D. J. & Doolan, C. J. 2014 A review of flow-induced noise from finite wall-mounted cylinders. J. Fluid Struct. 51, 240–254.Google Scholar
Prasad, A. K. & Jensen, K. 1995 Scheimpflug stereocamera for particle image velocimetry in liquid flows. Appl. Opt. 34, 7092–7099.Google Scholar
Qu, Y., Wang, J.-J., Sun, M., Feng, L.-H., Pan, C., Gao, Q. & He, G.-S. 2017 Wake vortex evolution of square cylinder with a slot synthetic jet positioned at the rear surface. J. Fluid Mech. 812, 940–965.Google Scholar
Roh, S. & Park, S. 2003 Vortical flow over the free end surface of a finite circular cylinder mounted on a flat plate. Exp. Fluids 34, 63–67.Google Scholar
Saeedi, M., Lepoudre, P. P. & Wang, B. C. 2014 Direct numerical simulation of turbulent wake behind a surface-mounted square cylinder. J. Fluid Struct. 51, 20–39.Google Scholar
Saeedi, M. & Wang, B.-C. 2016 Large-eddy simulation of turbulent flow around a finite-height wall-mounted square cylinder within a thin boundary layer. Flow Turbul. Combust. 1–26.Google Scholar
Sakamoto, H. & Arie, M. 1983 Vortex shedding from a rectangular prism and a circular cylinder placed vertically in a turbulent boundary layer. J. Fluid Mech. 126, 147–165.Google Scholar
Sattari, P., Bourgeois, J. A. & Martinuzzi, R. J. 2012 On the vortex dynamics in the wake of a finite surface-mounted square cylinder. Exp. Fluids 52, 1149–1167.CrossRefGoogle Scholar
Scarano, F. 2002 Iterative image deformation methods in PIV. Meas. Sci. Technol. 13, R1–R19.Google Scholar
Scarano, F. 2013 Tomographic PIV: principles and practice. Meas. Sci. Technol. 24, 012001.Google Scholar
Schäfer, F., Breuer, M. & Durst, F. 2009 The dynamics of the transitional flow over a backward-facing step. J. Fluid Mech. 623, 85–119.Google Scholar
Sujudi, D. & Haimes, R.1995 Identification of swirling flow in 3D vector fields. AIAA Paper 95-1715.Google Scholar
Sumner, D. & Heseltine, J. L. 2008 Tip vortex structure for a circular cylinder with a free end. J. Wind Engng Ind. Aerodyn. 96, 1185–1196.CrossRefGoogle Scholar
Sumner, D., Heseltine, J. L. & Dansereau, O. J. P. 2004 Wake structure of a finite circular cylinder of small aspect ratio. Exp. Fluids 37, 720–730.Google Scholar
Tadmor, G., Lehmann, O., Noack, B. R. & Morzyński, M. 2010 Mean field representation of the natural and actuated cylinder wake. Phys. Fluids 22, 034102.Google Scholar
Tsutsui, T. 2012 Flow around a cylindrical structure mounted in a plane turbulent boundary layer. J. Wind Engng Ind. Aerodyn. 104–106, 239–247.Google Scholar
Wang, C. Y., Gao, Q., Wang, H. P., Wei, R. J., Li, T. & Wang, J. J. 2016a Divergence-free smoothing for volumetric PIV data. Exp. Fluids 57, 1–23.CrossRefGoogle Scholar
Wang, C. Y., Gao, Q., Wei, R. J., Li, T. & Wang, J. J. 2016b 3D flow visualization and tomographic particle image velocimetry for vortex breakdown over a non-slender delta wing. Exp. Fluids 57, 1–13.CrossRefGoogle Scholar
Wang, H. F., Cao, H. L. & Zhou, Y. 2014a POD analysis of a finite-length cylinder near wake. Exp. Fluids 55, 1–15.Google Scholar
Wang, H. F., Zhou, Y., Chan, C. K. & Lam, K. S. 2006 Effect of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake. Phys. Fluids 18, 2451–2466.Google Scholar
Wang, H. F. & Zhou, Y. 2009 The finite-length square cylinder near wake. J. Fluid Mech. 638, 453–490.Google Scholar
Wang, Y. Q., Jackson, P. L. & Sui, J. 2014b Simulation of turbulent flow around a surface-mounted finite square cylinder. J. Thermophys Heat Transfer 28, 118–132.CrossRefGoogle Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45, 549–556.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar