Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T22:33:13.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Tip-vortex instability and turbulent mixing in wind-turbine wakes

Published online by Cambridge University Press:  23 September 2015

L. E. M. Lignarolo ,
D. Ragni ,
F. Scarano ,
C. J. Simão Ferreira  and
G. J. W. van Bussel
L. E. M. Lignarolo*
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HSDelft, The Netherlands
D. Ragni
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HSDelft, The Netherlands
F. Scarano
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HSDelft, The Netherlands
C. J. Simão Ferreira
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HSDelft, The Netherlands
G. J. W. van Bussel
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HSDelft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Kinetic-energy transport and turbulence production within the shear layer of a horizontal-axis wind-turbine wake are investigated with respect to their influence on the tip-vortex pairwise instability, the so-called leapfrogging instability. The study quantifies the effect of near-wake instability and tip-vortex breakdown on the process of mean-flow kinetic-energy transport within the far wake of the wind turbine, in turn affecting the wake re-energising process. Experiments are conducted in an open-jet wind tunnel with a wind-turbine model of 60 cm diameter at a diameter-based Reynolds number range 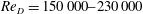$\mathit{Re}_{D}=150\,000{-}230\,000$. The velocity fields in meridian planes encompassing a large portion of the wake past the rotor are measured both in the unconditioned and the phase-locked mode by means of stereoscopic particle image velocimetry. The detailed topology and development of the tip-vortex interactions are discussed prior to a statistical analysis based on the triple decomposition of the turbulent flow fields. The study emphasises the role of the pairing instability as a precursor to the onset of three-dimensional vortex distortion and breakdown, leading to increased turbulent mixing and kinetic-energy transport across the shear layer. Quadrant analysis further elucidates the role of sweep and ejection events within the two identified mixing regimes. Prior to the onset of the instability, vortices shed from the blade appear to inhibit turbulent mixing of the expanding wake. The second region is dominated by the leapfrogging instability, with a sudden increase of the net entrainment of kinetic energy. Downstream of the latter, random turbulent motion characterises the flow, with a significant increase of turbulent kinetic-energy production. In this scenario, the leapfrogging mechanism is recognised as the triggering event that accelerates the onset of efficient turbulent mixing followed by the beginning of the wake re-energising process.

JFM classification

Mixing: Turbulent mixing Vortex Flows: Vortex instability Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 467 - 493
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akay, B., Ferreira, C. S., Van Bussel, G. J. W. & Herraez, I. 2012 Experimental and numerical quantification of radial flow in the root region of a HAWT. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, USA, American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Antonia, R. A. & Browne, L. W. B. 1987 Quadrant analysis in the turbulent far-wake of a cylinder. Fluid Dyn. Res. 2 (1), 3–14.Google Scholar
Antonia, R. A., Browne, L. W. B., Bisset, D. K. & Fulachier, L. 1987 A description of the organized motion in the turbulent far wake of a cylinder at low Reynolds number. J. Fluid Mech. 184, 423–444.Google Scholar
Antonia, R. A., Chambers, A. J., Britz, D. & Browne, L. W. B. 1986 Organized structures in a turbulent plane jet: topology and contribution to momentum and heat transport. J. Fluid Mech. 172, 211–229.Google Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22 (2), 129–136.Google Scholar
Bolnot, H., Le Dizès, S. & Leweke, T. 2014 Pairing instability in helical vortices. In Wind Energy – Impact of Turbulence, vol. 2, pp. 23–28. Springer.CrossRefGoogle Scholar
Bolnot, H., Leweke, T. & Le Dizès, S. 2011 Spatio-temporal development of the pairing instability in helical vortices. In Proceedings of the 6th AIAA Theoretical Fluid Mechanics Conference. Honolulu, Hawaii. AIAA.Google Scholar
Browand, F. K. & Weidman, P. D. 1976 Large scales in the developing mixing layer. J. Fluid Mech. 76 (01), 127–144.Google Scholar
Cal, R. B., Lebrón, J., Castillo, L., Kang, H. S. & Meneveau, C. 2010 Experimental study of the horizontally averaged flow structure in a model wind-turbine array boundary layer. J. Renew. Sustain. Energy 2, 013106.Google Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22 (1), 015110–015116.Google Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
Chamorro, L. P., Arndt, R. E. A. & Sotiropoulos, F. 2012 Reynolds number dependence of turbulence statistics in the wake of wind turbines. Wind Energy 15 (5), 733–742.Google Scholar
Crespo, A., Hernández, J. & Frandsen, S. 1999 Survey of modelling methods for wind turbine wakes and wind farms. Wind Energy 2 (1), 1–24.3.0.CO;2-7>CrossRefGoogle Scholar
Dobrev, I., Maalouf, B., Troldborg, N. & Massouh, F. 2008 Investigation of the wind turbine vortex structure. In Proceedings of the 14th International Symposium on Applications of Laser Techniques to Fluid Mechanics. Lisbon, Portugal.Google Scholar
Escudié, R. & Liné, A. 2003 Experimental analysis of hydrodynamics in a radially agitated tank. AIChE J. 49 (3), 585–603.CrossRefGoogle Scholar
Fabris, G. 1979 Conditional sampling study of the turbulent wake of a cylinder. Part 1. J. Fluid Mech. 94 (04), 673–709.Google Scholar
Felli, M., Camussi, R. & Di Felice, F. 2011 Mechanisms of evolution of the propeller wake in the transition and far fields. J. Fluid Mech. 682, 5–53.CrossRefGoogle Scholar
Ferreira, C. S.2009 The near wake of the VAWT: 2D and 3D views of the VAWT aerodynamics, Delft University of Technology.Google Scholar
Ghaemi, S. & Scarano, F. 2011 Counter–Hairpin vortices in the turbulent wake of a sharp trailing edge. J. Fluid Mech. 689, 317–356.Google Scholar
Hamilton, N., Kang, H. S., Meneveau, C. & Cal, R. B. 2012 Statistical analysis of kinetic energy entrainment in a model wind turbine array boundary layer. J. Renew. Sustain. Energy 4 (6), 063105–063119.CrossRefGoogle Scholar
Hattori, Y., Moeng, C.-H., Suto, H., Tanaka, N. & Hirakuchi, H. 2010 Wind-tunnel experiment on logarithmic-layer turbulence under the influence of overlying detached eddies. Boundary-Layer Meteorol. 134 (2), 269–283.CrossRefGoogle Scholar
Herpin, S., Wong, C. Y., Stanislas, M. & Soria, J. 2008 Stereoscopic PIV measurements of a turbulent boundary layer with a large spatial dynamic range. Exp. Fluids 45 (4), 745–763.Google Scholar
Humble, R. A.2008 Unsteady flow organisation of a shock wave/boundary layer interaction. Aerospace Engineering, Delft University of Technology.Google Scholar
Hussain, A. K. M. F. 1981 Role of coherent structures in turbulent shear flows. Proc. Indian Acad. Sci. C 4 (2), 129–175.CrossRefGoogle Scholar
Hussain, A. K. M. F. 1983 Coherent structures – reality and myth. Phys. Fluids 26 (10), 2816–2850.Google Scholar
Hütter, U. 1977 Optimum wind-energy conversion systems. Annu. Rev. Fluid Mech. 9, 399–419.Google Scholar
Ivanell, S.2009 Numerical computations of wind turbine wakes. Linne Flow Centre, Department of Mechanics. SE-100 44 Stockholm, Sweden, Royal Institute of Technology KTH – Gotland University.Google Scholar
Ivanell, S., Mikkelsen, R., Sørensen, J. N. & Henningson, D. 2010 Stability analysis of the tip vortices of a wind turbine. Wind Energy 13 (8), 705–715.CrossRefGoogle Scholar
Joukowsky, N. E. 1912 Vortex Theory of Screw Propeller. Gauthier-Villars.Google Scholar
Katul, G., Kuhn, G., Schieldge, J. & Hsieh, C.-I. 1997 The ejection-sweep character of scalar fluxes in the unstable surface layer. Boundary-Layer Meteorol. 83 (1), 1–26.Google Scholar
Katul, G., Poggi, D., Cava, D. & Finnigan, J. 2006 The relative importance of ejections and sweeps to momentum transfer in the atmospheric boundary layer. Boundary-Layer Meteorol. 120 (3), 367–375.Google Scholar
Leishman, J. G. 1998 Measurements of the aperiodic wake of a hovering rotor. Exp. Fluids 25 (4), 352–361.Google Scholar
Leweke, T., Bolnot, H., Quaranta, U. & Le Dizès, S. 2013 Local and global pairing in helical vortex systems. In Proceedings of the International Conference on Aerodynamics of Offshore Wind Energy Systems and Wakes Lyngby, Denmark.Google Scholar
Lignarolo, L. E. M., Ragni, D., Krishnaswami, C., Chen, Q., Simão Ferreira, C. J. & Van Bussel, G. J. W. 2014 Experimental analysis of the wake of a horizontal-axis wind-turbine model. Renew. Energy 70, 31–46.Google Scholar
Lugt, H. J. 1996 Introduction to Vortex Theory. Vortex Flow Press.Google Scholar
Medici, D.2005 Experimental Studies of Wind Turbine Wakes – Power Optimisation and Meandering. Mechanics. Stockholm, Royal Institute of Technology (KTH).Google Scholar
Odemark, Y. & Fransson, J. H. M. 2013 The stability and development of tip and root vortices behind a model wind turbine. Exp. Fluids 54 (9), 1–16.Google Scholar
Okulov, V. & Sorensen, J. 2004 Instability of a vortex wake behind wind turbines. Dokl. Phys. 49 (12), 772–777.Google Scholar
Okulov, V. L. 2004 On the stability of multiple helical vortices. J. Fluid Mech. 521, 319–342.CrossRefGoogle Scholar
Okulov, V. L. & Sorensen, J. N. 2007 Stability of helical tip vortices in a rotor far wake. J. Fluid Mech. 576, 1–25.Google Scholar
Pentek, A., Tel, T. & Toroczkai, T. 1995 Chaotic advection in the velocity field of leapfrogging vortex pairs. J. Phys. A: Math. Gen. 28 (8), 2191.Google Scholar
Poggi, D. & Katul, G. 2008 The effect of canopy roughness density on the constitutive components of the dispersive stresses. Exp. Fluids 45 (1), 111–121.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide. Springer Science & Business Media.Google Scholar
Ragni, D., Ashok, A., Van Oudheusden, B. W. & Scarano, F. 2009 Surface pressure and aerodynamic loads determination of a transonic airfoil based on particle image velocimetry. Meas. Sci. Technol. 20 (7), 074005.Google Scholar
Ragni, D., Oudheusden, B. W. & Scarano, F. 2011 Non-intrusive aerodynamic loads analysis of an aircraft propeller blade. Exp. Fluids 51 (2), 361–371.Google Scholar
Raupach, M. R. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (02), 263–288.CrossRefGoogle Scholar
Riley, N. & Stevens, D. P. 1993 A note on leapfrogging vortex rings. Fluid Dyn. Res. 11 (5), 235–244.Google Scholar
van Rooij, R. P. J. O. M. V.1996 Modification of the boundary layer calculation in RFOIL for improved airfoil stall prediction. Delft, Delft University of Technology.Google Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49, 371–380.Google Scholar
Schepers, J. G.2012 Engineering models in wind energy aerodynamics. PhD thesis, Aerospace Engineering, Delft University of Technology.Google Scholar
Schreck, S., Lundquist, J. & Shaw, W.2008 US Department of Energy Workshop Report Research needs for wind resource characterization. Golden, CO, National Renewable Energy Laboratory.Google Scholar
Selig, M. S., Guglielmo, J. J., Broeren, A. P. & Giguère, P. 1995 Summary of Low-Speed Airfoil Data. SoarTech.Google Scholar
Snel, H., Schepers, J. G. & Montgomerie, B. 2007 The MEXICO Project (model experiments in controlled conditions): The database and first results of data processing and interpretation. J. Phys.: Conf. Ser. 75 (1), 012014.Google Scholar
Sørensen, J. N. 2011 Instability of helical tip vortices in rotor wakes. J. Fluid Mech. 682, 1–4.Google Scholar
Stanislas, M., Perret, L. & Foucaut, J. M. 2008 Vortical structures in the turbulent boundary layer: a possible route to a universal representation. J. Fluid Mech. 602, 327–382.Google Scholar
Tophøj, L. & Aref, H. 2013 Instability of vortex pair leapfrogging. Phys. Fluids 25 (1), 014107.CrossRefGoogle Scholar
Vandernoot, F.-X., Barricau, P., Bézard, H. & Boisson, H.-C. 2008 Mean and turbulence measurements of wake vortices. Wandering effects. In Proceedings of the 14th International Symposium on Applications of Laser Techniques to Fluid Mechanics Lisbon, Portugal.Google Scholar
Vermeer, L. J., Sørensen, J. N. & Crespo, A. 2003 Wind turbine wake aerodynamics. Prog. Aeronaut. Sci. 39 (6–7), 467–510.Google Scholar
Violato, D. & Scarano, F. 2011 Three-dimensional evolution of flow structures in transitional circular and chevron jets. Phys. Fluids 23 (12), 124104.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (01), 39–48.Google Scholar
Westerweel, J. 1997 Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 8, 1379–1392.Google Scholar
Whale, J., Anderson, C. G., Bareiss, R. & Wagner, S. 2000 An experimental and numerical study of the vortex structure in the wake of a wind turbine. J. Wind Engng Ind. Aerodyn. 84 (1), 1–21.Google Scholar
White, F. M. 1991 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Widnall, S. E. 1972 The stability of a helical vortex filament. J. Fluid Mech. 54 (04), 641–663.Google Scholar
Widnall, S. E. & Sullivan, J. P. 1973 On the Stability of Vortex Rings. The Royal Society.Google Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55 (01), 65–92.Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63 (02), 237–255.Google Scholar
Yule, A. J. 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89 (03), 413–432.Google Scholar