Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T21:50:12.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Time-resolved flow dynamics and Reynolds number effects at a wall–cylinder junction

Published online by Cambridge University Press:  13 July 2015

Nikolaos Apsilidis ,
Panayiotis Diplas ,
Clinton L. Dancey  and
Polydefkis Bouratsis
Nikolaos Apsilidis*
Affiliation:
Baker Environmental Hydraulics Laboratory, Virginia Tech, Blacksburg, VA 24061, USA
Panayiotis Diplas
Affiliation:
Department of Civil and Environmental Engineering, Lehigh University, Bethlehem, PA 18015, USA
Clinton L. Dancey
Affiliation:
Baker Environmental Hydraulics Laboratory, Virginia Tech, Blacksburg, VA 24061, USA
Polydefkis Bouratsis
Affiliation:
Baker Environmental Hydraulics Laboratory, Virginia Tech, Blacksburg, VA 24061, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study investigated the physics of separated turbulent flows near the vertical intersection of a flat wall with a cylindrical obstacle. The geometry imposes an adverse pressure gradient on the incoming boundary layer. As a result, flow separates from the wall and reorganizes to a system of characteristic flow patterns known as the horseshoe vortex. We studied the time-averaged and instantaneous behaviour of the turbulent horseshoe vortex using planar time-resolved particle image velocimetry (TRPIV). In particular, we focused on the effect of Reynolds number based on the diameter of the obstacle and the bulk approach velocity, 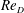$\mathit{Re}_{D}$. Experiments were carried out at 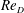$\mathit{Re}_{D}$: 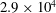$2.9\times 10^{4}$, 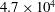$4.7\times 10^{4}$ and 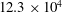$12.3\times 10^{4}$. Data analysis emphasized time-averaged and turbulence quantities, time-resolved flow dynamics and the statistics of coherent flow patterns. It is demonstrated that two large-scale vortical structures dominate the junction flow topology in a time-averaged sense. The number of additional vortices with intermittent presence does not vary substantially with 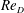$\mathit{Re}_{D}$. In addition, the increase of turbulence kinetic energy (TKE), momentum and vorticity content of the flow at higher 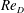$\mathit{Re}_{D}$ is documented. The distinctive behaviour of the primary horseshoe vortex for the 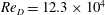$\mathit{Re}_{D}=12.3\times 10^{4}$ case is manifested by episodes of rapid advection of the vortex to the upstream, higher spatio-temporal variability of its trajectory, and violent eruptions of near-wall fluid. Differences between this experimental run and those at lower Reynolds numbers were also identified with respect to the spatial extents of the bimodal behaviour of the horseshoe vortex, which is a well-known characteristic of turbulent junction flows. Our findings suggest a modified mechanism for the aperiodic switching between the dominant flow modes. Without disregarding the limitations of this work, we argue that Reynolds number effects need to be considered in any effort to control the dynamics of junction flows characterized by the same (or reasonably similar) configurations.

JFM classification

Waves/Free-surface Flows: Hydraulics Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 475 - 511
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Agui, J. H. & Andreopoulos, Y. 1992 Experimental investigation of a three-dimensional boundary layer flow in the vicinity of an upright wall mounted cylinder. Trans. ASME: J. Fluids Engng 114, 566–576.Google Scholar
Allen, J. J. & Naitoh, T. 2007 Scaling and instability of a junction vortex. J. Fluid Mech. 574, 1–23.Google Scholar
Baker, C. J. 1979 The turbulent horseshoe vortex. J. Wind Engng Ind. Aerodyn. 6, 9–23.Google Scholar
Ballio, F., Bettoni, C. & Franzetti, S. 1998 Survey of time-averaged characteristics of laminar and turbulent horseshoe vortices (Data bank contribution). Trans. ASME J. Fluids Engng 120 (2), 233–242.Google Scholar
Dargahi, B. 1989 The turbulent flow field around a circular cylinder. Exp. Fluids 8 (1–2), 1–12.Google Scholar
Devenport, W. J. & Simpson, R. L. 1990 Time-dependent and time-averaged turbulence structure near the nose of a wing–body junction. J. Fluid Mech. 210, 23–55.Google Scholar
Eckerle, W. A. & Awad, J. K. 1991 Effect of freestream velocity on the 3-dimensional separated flow region in front of a cylinder. Trans. ASME: J. Fluids Engng 113 (1), 37–44.Google Scholar
Eckstein, A. C., Charonko, J. & Vlachos, P. P. 2008 Phase correlation processing for DPIV measurements. Exp. Fluids 45 (3), 485–500.Google Scholar
Eckstein, A. C. & Vlachos, P. P. 2009 Assessment of advanced windowing techniques for digital particle image velocimetry (DPIV). Meas. Sci. Technol. 20 (7), 075402.Google Scholar
Escauriaza, C. & Sotiropoulos, F. 2011a Initial stages of erosion and bed form development in a turbulent flow around a cylindrical pier. J. Geophys. Res. 116, F03007.Google Scholar
Escauriaza, C. & Sotiropoulos, F. 2011b Lagrangian model of bed-load transport in turbulent junction flows. J. Fluid Mech. 666, 36–76.Google Scholar
Escauriaza, C. & Sotiropoulos, F. 2011c Reynolds number effects on the coherent dynamics of the turbulent horseshoe vortex system. Flow Turbul. Combust. 86 (2), 231–262.Google Scholar
Etebari, A. & Vlachos, P. P. 2005 Improvements on the accuracy of derivative estimation from DPIV velocity measurements. Exp. Fluids 39 (6), 1040–1050.Google Scholar
Fleming, J. L., Simpson, R. L., Cowling, J. E. & Devenport, W. J. 1993 An experimental study of a turbulent wing body junction and wake flow. Exp. Fluids 14 (5), 366–378.CrossRefGoogle Scholar
Gand, F., Deck, S., Brunet, V. & Sagaut, P. 2010 Flow dynamics past a simplified wing body junction. Phys. Fluids 22 (11), 115111.Google Scholar
Honkanen, M. & Nobach, H. 2005 Background extraction from double-frame PIV images. Exp. Fluids 38 (3), 348–362.Google Scholar
Hunt, J. C. R., Abell, C. J., Peterka, J. A. & Woo, H. 1978 Kinematical studies of flows around free or surface-mounted obstacles – applying topology to flow visualization. J. Fluid Mech. 86 (1), 179–200.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases 2, vol. 1, pp. 193–208.Google Scholar
Ishii, J. & Honami, S. 1986 A three-dimensional turbulent detached flow with a horseshoe vortex. Trans. ASME: J. Engng Gas Turbines Power 108 (1), 125–130.Google Scholar
Kirkil, G. & Constantinescu, G. 2009 Nature of flow and turbulence structure around an in-stream vertical plate in a shallow channel and the implications for sediment erosion. Water Resour. Res. 45, W06412.CrossRefGoogle Scholar
Kirkil, G., Constantinescu, G. & Ettema, R. 2006 Investigation of the velocity and pressure fluctuations distributions inside the turbulent horseshoe vortex system around a circular bridge pier. In River Flow 2006, pp. 709–718. Taylor & Francis/A. A. Balkema.Google Scholar
Koken, M. & Constantinescu, G. 2009 An investigation of the dynamics of coherent structures in a turbulent channel flow with a vertical sidewall obstruction. Phys. Fluids 21 (8), 085104.Google Scholar
Ölçmen, S. M. & Simpson, R. L. 1994 Influence of wing shapes on surface pressure fluctuations at wing–body junctions. AIAA J. 32 (1), 6–15.CrossRefGoogle Scholar
Paik, J., Escauriaza, C. & Sotiropoulos, F. 2007 On the bimodal dynamics of the turbulent horseshoe vortex system in a wing–body junction. Phys. Fluids 19 (4), 115104.Google Scholar
Praisner, T. J., Seal, C. V., Takmaz, L. & Smith, C. R. 1997 Spatial-temporal turbulent flow-field and heat transfer behavior in end-wall junctions. Intl J. Heat Fluid Flow 18 (1), 142–151.Google Scholar
Praisner, T. J. & Smith, C. R. 2006a The dynamics of the horseshoe vortex and associated endwall heat transfer – part I: temporal behavior. Trans. ASME: J. Turbomach. 128 (4), 747–754.Google Scholar
Praisner, T. J. & Smith, C. R. 2006b The dynamics of the horseshoe vortex and associated endwall heat transfer – part II: time-mean results. Trans. ASME: J. Turbomach. 128 (4), 755–762.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2007 Particle Image Velocimetry – A Practical Guide, 2nd edn. Springer.Google Scholar
Rodi, W. 1997 Comparison of LES and RANS calculations of the flow around bluff bodies. J. Wind Engng Ind. Aerodyn. 69–71, 55–75.CrossRefGoogle Scholar
Roulund, A., Sumer, B. M., Fredsøe, J. & Michelsen, J. 2005 Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 534, 351–401.Google Scholar
Sabatino, D. R. & Smith, C. R. 2009 Boundary layer influence on the unsteady horseshoe vortex flow and surface heat transfer. Trans. ASME: J. Turbomach. 131 (1), 011015.Google Scholar
Shavit, U., Lowe, R. & Steinbuck, J. 2007 Intensity capping: a simple method to improve cross-correlation PIV results. Exp. Fluids 42 (2), 225–240.Google Scholar
Simpson, R. L. 2001 Junction flows. Annu. Rev. Fluid Mech. 33, 415–443.Google Scholar
Wallace, J. M. & Foss, J. F. 1995 The measurement of vorticity in turbulent flows. Annu. Rev. Fluid Mech. 27 (1), 469–514.Google Scholar
Westerweel, J. 1997 Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 8, 1379–1392.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.Google Scholar