Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T14:46:39.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Time evolution of uniform momentum zones in a turbulent boundary layer

Published online by Cambridge University Press:  13 March 2018

A. Laskari Open the ORCID record for A. Laskari [Opens in a new window] ,
R. de Kat Open the ORCID record for R. de Kat [Opens in a new window] ,
R. J. Hearst Open the ORCID record for R. J. Hearst [Opens in a new window]  and
B. Ganapathisubramani
A. Laskari
Affiliation:
Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
R. de Kat
Affiliation:
Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
R. J. Hearst
Affiliation:
Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK Department of Energy and Process Engineering, Norwegian University of Science and Technology, Trondheim, Norway
B. Ganapathisubramani*
Affiliation:
Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Time-resolved planar particle image velocimetry was used to analyse the structuring of a turbulent boundary layer into uniform momentum zones (UMZs). The instantaneous peak-detection method employed by Adrian et al. (J. Fluid Mech., vol. 422, 2000, pp. 1–54) and de Silva et al. (J. Fluid Mech., vol. 786, 2016, pp. 309–331) is extended to account for temporal coherence of UMZs. The resulting number of zones detected appears to follow a normal distribution at any given instant. However, the extreme cases in which the number of zones is either very high or very low, are shown to be linked with two distinct flow states. A higher than average number of zones is associated with a large-scale 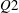$Q2$ event in the log region which creates increased small-scale activity within that region. Conversely, a low number of zones corresponds to a large-scale 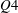$Q4$ event in the log region and decreased turbulent activity away from the wall. The residence times, within the measurement plane, of zones belonging to the latter scenario are shown to be on average four times larger than those of zones present during higher than average zone structuring states. For both cases, greater residence times are observed for zones of higher momentum that are generally closer to the free stream.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 554 - 590
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Ahn, Junsun, Lee, J. H., Lee, J., Kang, J.-H. & Sung, H. J. 2015 Direct numerical simulation of a 30r long turbulent pipe flow at Re = 3008. Phys. Fluids 27 (6), 065110.Google Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.CrossRefGoogle Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.Google Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014a Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 298–328.Google Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014b The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21 (2), 91–108.Google Scholar
Corino, E. R. & Brodkey, R. S. 1969 A visual investigation of the wall region in turbulent flow. J. Fluid Mech. 37, 1–30.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep.Google Scholar
Davoust, S. & Jacquin, L. 2011 Taylor’s hypothesis convection velocities from mass conservation equation. Phys. Fluids 23 (5), 051701.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Eisma, J., Westerweel, J., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27 (5), 055103.Google Scholar
Fisher, M. J. & Davies, P. O. A. L. 1964 Correlation measurements in a non-frozen pattern of turbulence. J. Fluid Mech. 18, 97–116.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Geng, C., He, G., Wang, Y., Xu, C., Lozano-Durán, Á. & Wallace, J. M. 2015 Taylor’s hypothesis in turbulent channel flow considered using a transport equation analysis. Phys. Fluids 27 (2), 025111.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.CrossRefGoogle Scholar
Hellström, L. H. O., Ganapathisubramani, B. & Smits, A. J. 2015 The evolution of large-scale motions in turbulent pipe flow. J. Fluid Mech. 779, 701–715.Google Scholar
Hunt, J. C., Eames, I. & Westerweel, J. 2006 Mechanics of inhomogeneous turbulence and interfacial layers. J. Fluid Mech. 554, 499–519.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Ishihara, T., Ogasawara, H. & Hunt, J. C. R. 2015 Analysis of conditional statistics obtained near the turbulent/non-turbulent interface of turbulent boundary layers. J. Fluids Struct. 53, 50–57; Special Issue on Unsteady Separation in Fluid-Structure Interaction II.Google Scholar
JCGM2008 Evaluation of measurement data – Guide to the expression of uncertainty in measurement (GUM 1995 with minor corrections). Tech. Rep. Joint Committee for Guides in Metrology.Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.CrossRefGoogle Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.Google Scholar
Khashehchi, M., Ooi, A., Soria, J. & Marusic, I. 2013 Evolution of the turbulent/non-turbulent interface of an axisymmetric turbulent jet. Exp. Fluids 54 (1), 1–12.CrossRefGoogle Scholar
Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50, 133–160.Google Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids A 5 (3), 695–706.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.Google Scholar
Kwon, Y. S., Philip, J., de Silva, C. M., Hutchins, N. & Monty, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
Lozano-Duran, A., Flores, O. & Jimenez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Offen, G. R. & Kline, S. J. 1975 A proposed model of the bursting process in turbulent boundary layers. J. Fluid Mech. 70, 209–228.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Phillips, O. M. 1955 The irrotational motion outside a free turbulent boundary. Math. Proc. Camb. Phil. Soc. 51, 220–229.Google Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27 (8), 084006.Google Scholar
de Silva, C., Marusic, I. & Hutchins, N. 2014 Regions of uniform streamwise momentum in turbulent boundary layers. In Proceedings of the 19th Australasian Fluid Mechanics Conference, RMIT University, Melbourne, Australia.Google Scholar
da Silva, C. B., dos Reis, R. J. N. & Pereira, J. C. F. 2011 The intense vorticity structures near the turbulent/non-turbulent interface in a jet. J. Fluid Mech. 685, 165–190.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.Google Scholar
Spalding, D. B. 1961 A single formula for the law of the wall. Trans. ASME J. Appl. Mech. 28 (3), 455–458.Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the 2nd Midwestern Conference of Fluid Mechanics, Ohio State University, Colombus, OH.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.CrossRefGoogle Scholar
Townsend, A. A. 1949 Momentum and energy diffusion in the turbulent wake of a cylinder. Proc. R. Soc. Lond. A 197 (1048), 124–140.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.CrossRefGoogle Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015 Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.CrossRefGoogle Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.CrossRefGoogle Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1981 Taylor hypothesis and large-scale coherent structures. J. Fluid Mech. 112, 379–396.CrossRefGoogle Scholar
Zheng, S. & Longmire, E. 2014 Perturbing vortex packets in a turbulent boundary layer. J. Fluid Mech. 748, 368–398.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, R. S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar

Laskari et al. supplementary movie 1

Time evolution of all instantaneously detected zones. For the time-sequence of velocity contours (left), the resulting probability density function (pdf) of U is shown in the middle. The peaks of the pdf (representing modal velocities) are marked with coloured symbols (colours according to the velocity value at each peak) for time coherent zones, and grey symbols for short-lived ones. The velocities marking the edge of the zones are shown with dashed lines on the pdf and correspond to the black solid lines demarkating each zone in physical space on the right. The time evolution of the thickness of each zone is presented on the right, where each zone is coloured according to its modal velocity.

Download Laskari et al. supplementary movie 1(Video)
Video 1.8 MB

Laskari et al. supplementary movie 2

Time evolution and ranking of time-coherent zones. For the time-sequence of velocity contours (left), the resulting probability density function (pdf) of U is shown in the middle for the same sequence as in movie 1, with all short-lived peaks removed. The remaining peaks for the time coherent zones are ranked in ascending order according to their momentum deficit level, effectively labelling the zone closest to the freestream as rank one, while the rank of the zone closest to the wall is equal to the total number of zones present in that particular image. Symbols denote different ranks. The time evolution of the thickness of each zone is presented on the right, where each zone is coloured according to its rank.

Download Laskari et al. supplementary movie 2(Video)
Video 1.6 MB