Published online by Cambridge University Press: 02 November 2017
The incompressible flow of a uniform fluid, which fills a rigid spheroid rotating about an arbitrary axis fixed in an inertial frame, is dominated at small Rossby and Ekman numbers by the rotation through the Coriolis force. The effects of rotation on the flow can be found by treating the Coriolis force modified by a pressure gradient as a skew-symmetric bounded linear operator 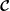 $\boldsymbol{{\mathcal{C}}}$ acting on smooth inviscid incompressible flows in the spheroid. It is shown that the space of incompressible polynomial flows of degree
$\boldsymbol{{\mathcal{C}}}$ acting on smooth inviscid incompressible flows in the spheroid. It is shown that the space of incompressible polynomial flows of degree 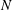 $N$ or less in the spheroid is invariant under
$N$ or less in the spheroid is invariant under 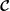 $\boldsymbol{{\mathcal{C}}}$ for any
$\boldsymbol{{\mathcal{C}}}$ for any 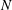 $N$. The skew symmetry of
$N$. The skew symmetry of 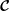 $\boldsymbol{{\mathcal{C}}}$ implies the Coriolis operator
$\boldsymbol{{\mathcal{C}}}$ implies the Coriolis operator 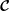 $\boldsymbol{{\mathcal{C}}}$ is non-defective for such flows with an orthogonal set of eigenmodes (inertial and geostrophic modes) which form a basis for the finite-dimensional space of spheroidal polynomial flows. The eigenmodes are tilted if the rotation axis is not aligned with the symmetry axis of the spheroid. The non-defective property of
$\boldsymbol{{\mathcal{C}}}$ is non-defective for such flows with an orthogonal set of eigenmodes (inertial and geostrophic modes) which form a basis for the finite-dimensional space of spheroidal polynomial flows. The eigenmodes are tilted if the rotation axis is not aligned with the symmetry axis of the spheroid. The non-defective property of 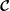 $\boldsymbol{{\mathcal{C}}}$ enables enumeration of the modes and proof of their completeness using the Weierstrass polynomial approximation theorem. The fundamental tool, which is required to establish invariance of spheroidal polynomial flows under
$\boldsymbol{{\mathcal{C}}}$ enables enumeration of the modes and proof of their completeness using the Weierstrass polynomial approximation theorem. The fundamental tool, which is required to establish invariance of spheroidal polynomial flows under 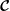 $\boldsymbol{{\mathcal{C}}}$ and completeness of the Coriolis modes, is that the solution of the polynomial Poisson–Neumann problem, i.e. Poisson’s equation with Neumann boundary condition and polynomial data, in a spheroid is a polynomial. The Coriolis modes of degree one and all geostrophic modes are explicitly constructed. Only the modes of degree one have non-zero angular momentum in the boundary frame.
$\boldsymbol{{\mathcal{C}}}$ and completeness of the Coriolis modes, is that the solution of the polynomial Poisson–Neumann problem, i.e. Poisson’s equation with Neumann boundary condition and polynomial data, in a spheroid is a polynomial. The Coriolis modes of degree one and all geostrophic modes are explicitly constructed. Only the modes of degree one have non-zero angular momentum in the boundary frame.