Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T05:40:13.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Threshold shear stress for the transition between tumbling and tank-treading of red blood cells in shear flow: dependence on the viscosity of the suspending medium

Published online by Cambridge University Press:  06 November 2013

Thomas M. Fischer  and
Rafal Korzeniewski
Thomas M. Fischer*
Affiliation:
Department of Physiology, RWTH Aachen University, Pauwelsstr. 30, 52074 Aachen, Germany
Rafal Korzeniewski
Affiliation:
Department of Physiology, RWTH Aachen University, Pauwelsstr. 30, 52074 Aachen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Red blood cells are the subject of diverse studies. One branch is the observation and theoretical modelling of their behaviour in a shear flow. This work deals with the flow of single red cells suspended in solutions much more viscous than blood plasma. Below a critical shear rate (${\dot {\gamma } }_{t} $) the red cells rotate with little change of their resting shape. Above that value they become elongated and aligned in the shear field. We measured 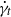${\dot {\gamma } }_{t} $ at viscosities (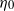${\eta }_{0} $) ranging from 10.7 to 104 mPa s via observation along the vorticity of a Poiseuille flow in a glass capillary; 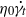${\eta }_{0} {\dot {\gamma } }_{t} $ decreased steeply with increasing 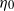${\eta }_{0} $ up to a value of 25 mPa s and remained constant for higher values. Present theoretical models are not in keeping with the measured data. Modifications of basic model assumptions are suggested.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Capsule/cell dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 736 , 10 December 2013 , pp. 351 - 365
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abkarian, M., Faivre, M. & Viallat, A. 2007 Swinging of red blood cells under shear flow. Phys. Rev. Lett. 98, 188302.CrossRefGoogle ScholarPubMed
Basu, H, Dharmadhikari, A. K., Dharmadhikari, J. A., Sharma, S. & Mathur, D. 2011 Tank treading of optically trapped red blood cells in shear flow. Biophys. J. 101, 1604–1612.CrossRefGoogle ScholarPubMed
Bessis, M. 1972 Red cell shapes: an illustrated classification and its rationale. Nouvelle Revue Française d’Hématologie 12, 721–746.Google ScholarPubMed
Betz, T., Lenz, M., Joanny, J.-F. & Sykes, C. 2009 ATP-dependent mechanics of red blood cells. Proc. Natl Acad. Sci. 106, 15320–15325.CrossRefGoogle ScholarPubMed
Bitbol, M. 1986 Red blood cell orientation in orbit $C= 0$ . Biophys. J. 49, 1055–1068.CrossRefGoogle ScholarPubMed
Boss, D., Hoffmann, A., Rappaz, B., Depeursinge, C. & Magistretti, P. J. 2012 Spatially-resolved eigenmode decomposition of red blood cells membrane fluctuations questions the role of ATP in flickering. PLoS ONE 7, e40667.CrossRefGoogle ScholarPubMed
Dimitrakopoulos, P. 2012 Analysis of the variation in the determination of the shear modulus of the erythrocyte membrane: effects of the constitutive law and membrane modelling. Phys. Rev. E 85, 041917.CrossRefGoogle Scholar
Dupire, J., Socol, M. & Viallat, A. 2012 Full dynamics of a red blood cell in shear flow. Proc. Natl Acad. Sci. USA 109, 20808–20813.CrossRefGoogle ScholarPubMed
Evans, E. & Fung, Y.-C. 1972 Improved measurements of the erythrocyte geometry. Microvasc. Res. 4, 335–347.CrossRefGoogle ScholarPubMed
Evans, J., Gratzer, W., Mohandas, N., Parker, K. & Sleep, J. 2008 Fluctuations of the red blood cell membrane: relation to mechanical properties and lack of ATP dependence. Biophys. J. 94, 4134–4144.CrossRefGoogle ScholarPubMed
Fedosov, D. A., Caswell, B. & Karniadakis, G. E 2010a Dissipative particle dynamics modelling of red blood cells. In Red Cell Membrane Transport in Health and Disease (ed. Pozrikidis, C.), pp. 182–218. CRC Press.Google Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010b A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 98, 2215–2225.CrossRefGoogle ScholarPubMed
Fischer, T. M. 1980 On the energy dissipation in a tank-treading human red blood cell. Biophys. J. 61, 863–868.CrossRefGoogle Scholar
Fischer, T. M. 2004 Shape memory of human red blood cells. Biophys. J. 86, 3304–3313.CrossRefGoogle ScholarPubMed
Fischer, T. M. 2010 A method to prepare isotonic dextran–salt solutions. Cytometry A 77, 805–810.CrossRefGoogle ScholarPubMed
Fischer, T. M., Haest, C. W. M., Stöhr-Liesen, M., Schmid-Schönbein, H. & Skalak, R. 1981 The stress-free shape of the red blood cell membrane. Biophys. J. 34, 409–422.CrossRefGoogle ScholarPubMed
Fischer, T. M. & Korzeniewski, R. 2011 Effects of shear rate and suspending medium viscosity on elongation of red cells tank-treading in shear flow. Cytometry A 79, 946–951.CrossRefGoogle ScholarPubMed
Goldsmith, H. L. & Marlow, J. 1972 Flow behaviour of erythrocytes. Part 1. Rotation and deformation in dilute suspensions. Proc. R. Soc. Lond. B 182, 351–384.Google Scholar
Hochmuth, R. M., Worthy, P. R. & Evans, E. A. 1979 Red cell extensional recovery and the determination of membrane viscosity. Biophys. J. 26, 101–114.CrossRefGoogle ScholarPubMed
Huang, W.-X., Chang, C. B. & Sung, H. J. 2012 Three-dimensional simulation of elastic capsules in shear flow by the penalty immersed boundary method. J. Comput. Phys. 231, 3340–3364.CrossRefGoogle Scholar
Kaoui, B., Kruger, T. & Harting, J. 2012 How does confinement affect the dynamics of viscous vesicles and red blood cells?. Soft Matt. 8, 9246–9252.CrossRefGoogle Scholar
Keller, S. R. & Skalak, R. 1982 Motion of a tank-treading ellipsoidal particle in a shear flow. J. Fluid Mech. 120, 27–47.CrossRefGoogle Scholar
Le, D. V. 2010 Effect of bending stiffness on the deformation of liquid capsules enclosed by thin shells in shear flow. Phys. Rev. E 82, 016318.CrossRefGoogle ScholarPubMed
Le, D.-V. & Tan, Z. 2010 Large deformation of liquid capsules enclosed by thin shells immersed in the fluid. J. Comput. Phys. 229, 4097–4116.CrossRefGoogle Scholar
Lim, G. H. W., Wortis, M. & Mukhopadhyay, R. 2002 Stomatocyte–discocyte–echinocyte sequence of the human red blood cell: evidence for the bilayer-couple hypothesis from membrane mechanics. Proc. Natl Acad. Sci. USA 99, 16766–16769.CrossRefGoogle Scholar
Linderkamp, O. & Meiselman, H. J. 1982 Geometric, osmotic, and membrane mechanical properties of density-separated human red cells. Blood 59, 1121–1127.CrossRefGoogle ScholarPubMed
Morris, D. R. & Williams, A. R. 1979 The effects of suspending medium viscosity on erythrocyte deformation and haemolysis in vitro . Biochim. Biophys. Acta 550, 288–296.CrossRefGoogle ScholarPubMed
Noguchi, H. 2009 Swinging and synchronized rotations of red blood cells in simple shear flow. Phys. Rev. E 80, 021902.CrossRefGoogle ScholarPubMed
Park, Y., Best, C. A., Badizadegan, K., Dasari, R. R., Feld, M. S., Kuriabova, T., Henle, M. L., Levine, A. J. & Popescu, G. 2010 Measurement of red blood cell mechanics during morphological changes. Proc. Natl Acad. Sci. 107, 6731–6736.CrossRefGoogle ScholarPubMed
Schmid-Schönbein, H. & Wells, R. 1969 Fluid drop-like transition of erythrocytes under shear. Science 165, 288–291.CrossRefGoogle Scholar
Secomb, T. W. & Skalak, R. 1982 Surface flow of viscoelastic membranes in viscous fluids. Q. J. Mech. Appl. Maths 35, 233–247.CrossRefGoogle Scholar
Skalak, R., Tözeren, A., Zarda, P. & Chien, S. 1973 Strain energy function of red blood cell membranes. Biophys. J. 13, 245–264.CrossRefGoogle ScholarPubMed
Skotheim, J. M. & Secomb, T. W. 2007 Red blood cells and other nonspherical capsules in shear flow: oscillatory dynamics and the tank-treading-to-tumbling transition. Phys. Rev. Lett. 98, 078301.CrossRefGoogle ScholarPubMed
Tran-Son-Tay, R., Sutera, S. P. & Rao, P. R. 1984 Determination of red blood cell membrane viscosity from rheoscopic observations of tank-treading motion. Biophys. J. 46, 65–72.CrossRefGoogle ScholarPubMed
Tuvia, S., Almagor, A., Bitler, A., Levin, S., Korenstein, R. & Yedgar, S. 1997 Cell membrane fluctuations are regulated by medium macroviscosity: evidence for a metabolic driving force. Proc. Natl Acad. Sci. USA 94, 5045–5049.CrossRefGoogle ScholarPubMed
Vlahovska, P. M., Young, Y.-N., Danker, G. & Misbah, C. 2011 Dynamics of a non-spherical microcapsule with incompressible interface in shear flow. J. Fluid Mech. 678, 221–247.CrossRefGoogle Scholar
Yazdani, A. Z. K. & Bagchi, P. 2011 Phase diagram and breathing dynamics of a single red blood cell and a biconcave capsule in dilute shear flow. Phys. Rev. E 84, 026314.CrossRefGoogle Scholar
Yoon, Y.-Z., Hong, H., Brown, A., Kim, D. C., Kang, D. J., Lew, V. L. & Cicuta, P. 2009 Flickering analysis of erythrocyte mechanical properties: dependence on oxygenation level, cell shape, and hydration level. Biophys. J. 97, 1606–1615.CrossRefGoogle ScholarPubMed
Supplementary material: PDF

Fischer and Korzeniewski Supplementary Material

Supplementary Material

Download Fischer and Korzeniewski Supplementary Material(PDF)
PDF 220.6 KB