Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T14:28:46.546Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensionality of elliptical cylinder wakes at low angles of incidence

Published online by Cambridge University Press:  20 July 2017

Anirudh Rao Open the ORCID record for Anirudh Rao [Opens in a new window] ,
Justin S. Leontini ,
Mark C. Thompson  and
Kerry Hourigan
Anirudh Rao
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, 17 College Walk, Monash University, Clayton, Victoria 3800, Australia
Justin S. Leontini
Affiliation:
Department of Mechanical and Product Design Engineering, Swinburne University of Technology, John Street, Hawthorn, Victoria 3122, Australia
Mark C. Thompson*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, 17 College Walk, Monash University, Clayton, Victoria 3800, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, 17 College Walk, Monash University, Clayton, Victoria 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The wake of an elliptical cylinder at low incident angles is investigated for different aspect ratio (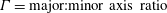$\unicode[STIX]{x1D6E4}=\text{major:minor axis ratio}$) cylinders using stability analysis and direct simulations. In particular, two- and three-dimensional transitions are mapped for cylinders of aspect ratios between 1 and 4 using Floquet stability analysis. The transition scenario for near-unity aspect ratio cylinders resembles that for a circular cylinder wake as Reynolds number is increased to 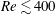$Re\lesssim 400$; first, with the transition from steady two-dimensional flow to unsteady two-dimensional flow, followed by the onset of three-dimensional flow via a long-wavelength instability (mode A), then, a short-wavelength instability (mode B) and, finally, an intermediary wavelength instability which is quasi-periodic in nature (mode QP). The effect of the incident angle on this transition scenario for the low-aspect-ratio cylinders is minimal. As the aspect ratio is increased towards 2, two synchronous modes, modes 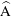$\widehat{\text{A}}$ and 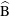$\widehat{\text{B}}$, become unstable; these modes have spatio-temporal symmetries similar to their circular cylinder wake counterparts, modes A and mode B, respectively. While mode 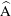$\widehat{\text{A}}$ persists for all incident angles investigated here, mode 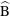$\widehat{\text{B}}$ is found only to be unstable for incident angles up to 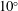$10^{\circ }$. Surprisingly, for 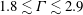$1.8\lesssim \unicode[STIX]{x1D6E4}\lesssim 2.9$, the mode A instability observed at zero incident angle emerges as a quasi-periodic mode as the incident angle is increased even slightly. At higher incident angles, this quasi-periodic mode once again transforms to a real mode on increasing the Reynolds number. The parameter space maps for the various aspect ratios are presented in the Reynolds number–incident angle plane, and the three-dimensional modes are discussed in terms of similarities to and differences from existing modes. A key aim of the work is to map the different modes and various transition sequences as a simple body geometry is systematically changed and as the flow symmetry is systematically broken; thus, insight is provided on the overall path towards fully turbulent flow.

JFM classification

Instability: Parametric instability Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 245 - 283
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbar, T., Bouchet, G. & Dušek, J. 2011 Numerical investigation of the subcritical effects at the onset of three-dimensionality in the circular cylinder wake. Phys. Fluids 23 (9), 094103.CrossRefGoogle Scholar
Akbar, T., Bouchet, G. & Dušek, J. 2014 Co-existence of A and B modes in the cylinder wake at Re = 170. Eur. J. Mech. (B/Fluids) 48, 19–26.CrossRefGoogle Scholar
Badr, H. M., Dennis, S. C. R. & Kocabiyik, S. 2001 Numerical simulation of the unsteady flow over an elliptic cylinder at different orientations. Intl J. Numer. Meth. Fluids 37 (8), 905–931.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Barkley, D., Tuckerman, L. S. & Golubitsky, M. 2000 Bifurcation theory for three-dimensional flow in the wake of a circular cylinder. Phys. Rev. E 61, 5247–5252.Google ScholarPubMed
Behara, S. & Mittal, S. 2010 Flow past a circular cylinder at low Reynolds number: oblique vortex shedding. Phys. Fluids 22 (5), 054102.CrossRefGoogle Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15, L57–L60.Google Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 552, 395–411.Google Scholar
Blackburn, H. M. & Sheard, G. J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22 (3), 031701,1–4.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics, 2nd edn. Springer.Google Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.CrossRefGoogle Scholar
Choi, C. B. & Yang, K. S. 2014 Three-dimensional instability in flow past a rectangular cylinder ranging from a normal flat plate to a square cylinder. Phys. Fluids 26 (6), 061702.Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22, 745–762.Google Scholar
Griffith, M. D., Jacono, D. L., Sheridan, J. & Leontini, J. S. 2016 Passive heaving of elliptical cylinders with active pitching – from cylinders towards flapping foils. J. Fluids Struct. 67, 124–141.Google Scholar
Griffith, M. D., Thompson, M. C., Leweke, T., Hourigan, K. & Anderson, W. P. 2007 Wake behaviour and instability of flow through a partially blocked channel. J. Fluid Mech. 582, 319–340.CrossRefGoogle Scholar
Jackson, C. P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.Google Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017 Two- and three-dimensional instabilities in the wake of a circular cylinder near a moving wall. J. Fluid Mech. 812, 435–462.Google Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016a Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.Google Scholar
Jiang, H., Cheng, L., Tong, F., Draper, S. & An, H. 2016b Stable state of mode A for flow past a circular cylinder. Phys. Fluids 28 (10), 104103.CrossRefGoogle Scholar
Johnson, S. A., Thompson, M. C. & Hourigan, K. 2004 Predicted low frequency structures in the wake of elliptical cylinders. Eur. J. Mech. (B/Fluids) 23 (1), 229–239.Google Scholar
Jones, M. C., Hourigan, K. & Thompson, M. C. 2015 A study of the geometry and parameter dependence of vortex breakdown. Phys. Fluids 27, 044102.Google Scholar
Jung, J. H. & Yoon, H. S. 2014 Large eddy simulation of flow over a twisted cylinder at a subcritical Reynolds number. J. Fluid Mech. 759, 579–611.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/hp Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
Kim, M.-S. & Park, Y.-B. 2006 Unsteady lift and drag forces acting on the elliptic cylinder. J. Mech. Sci. Technol. 20 (1), 167–175.Google Scholar
Kim, M.-S. & Sengupta, A. 2005 Unsteady viscous flow over elliptic cylinders at various thickness with different Reynolds numbers. J. Mech. Sci. Technol. 19 (3), 877–886.Google Scholar
Kim, W., Lee, J. & Choi, H. 2016 Flow around a helically twisted elliptic cylinder. Phys. Fluids 28 (5), 053602.Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2015 Stability analysis of the elliptic cylinder wake. J. Fluid Mech. 763, 302–321.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.Google Scholar
Lindsey, W. F.1937 Drag of cylinders of simple shapes. Tech. Rep. 619. National Advisory Committee for Aeronautics.Google Scholar
Ling, G. C. & Zhao, H. L. 2009 Vortex dislocations in wake-type flow induced by spanwise disturbances. Phys. Fluids 21 (7), 073604.Google Scholar
Lugt, H. J. & Haussling, H. J.1972 Laminar flows past elliptic cylinders at various angles of attack. Tech. Rep. 3748. Naval Ship Research And Development Center.Google Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf-bifurcation in spherical Couette flow. Phys. Fluids 7 (1), 80–91.Google Scholar
Marques, F., Lopez, J. M. & Blackburn, H. M. 2004 Bifurcations in systems with Z 2 spatio-temporal and O (2) spatial symmetry. Physica D 189, 247–276.CrossRefGoogle Scholar
Meneghini, J. R., Carmo, B. S., Tsiloufas, S. P., Gioria, R. S. & Aranha, J. A. P. 2011 Wake instability issues: from circular cylinders to stalled airfoils. J. Fluids Struct. 27 (56), 694–701; {IUTAM} Symposium on Bluff Body Wakes and Vortex-Induced Vibrations (BBVIV-6).Google Scholar
Mittal, R. & Balachandar, S. 1996 Direct numerical simulation of flow past elliptic cylinders. J. Comput. Phys. 124 (2), 351–367.Google Scholar
Mittal, S. & Sidharth, G. S. 2014 Steady forces on a cylinder with oblique vortex shedding. J. Fluids Struct. 44, 310–315.Google Scholar
Mori, T., Yoshikawa, H. & Ota, T. 2003 Unsteady flow around an elliptic cylinder in the critical Reynolds number regime. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, vol. 1, pp. 677–682.Google Scholar
Naik, S. N., Vengadesan, S. & Prakash, K. A. 2017 Numerical study of fluid flow past a rotating elliptic cylinder. J. Fluids Struct. 68, 15–31.Google Scholar
Nair, M. T. & Sengupta, T. K. 1997 Unsteady flow past elliptical cylinders. J. Fluids Struct. 11 (6), 555–595.Google Scholar
Navrose, M. J. & Mittal, S. 2015 Three-dimensional flow past a rotating cylinder. J. Fluid Mech. 766, 28–53.Google Scholar
Ng, Z. Y., Vo, T., Hussam, W. K. & Sheard, G. J. 2016 Linear instabilities in the wakes of cylinders with triangular cross-sections. In 20th Australasian Fluid Mechanics Conference (ed. Jones, N., Ivey, G., Zhou, T. & Draper, S.). Australasian Fluid Mechanics Society.Google Scholar
Paul, I., Prakash, K. A. & Vengadesan, S. 2014a Numerical analysis of laminar fluid flow characteristics past an elliptic cylinder: A parametric study. Intl J. Numer. Meth. Heat Fluid Flow 24 (7), 1570–1594.Google Scholar
Paul, I., Prakash, K. A. & Vengadesan, S. 2014b Onset of laminar separation and vortex shedding in flow past unconfined elliptic cylinders. Phys. Fluids 26 (2), 023601,1–15.Google Scholar
Radi, A., Thompson, M. C., Rao, A., Hourigan, K. & Sheridan, J. 2013 Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder. J. Fluid Mech. 734, 567–594.Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.CrossRefGoogle Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013b Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.CrossRefGoogle Scholar
Rao, A., Passaggia, P.-Y., Bolnot, H., Thompson, M. C., Leweke, T. & Hourigan, K. 2012 Transition to chaos in the wake of a rolling sphere. J. Fluid Mech. 695, 135–148.Google Scholar
Rao, A., Radi, A., Leontini, J. S., Thompson, M. C., Sheridan, J. & Hourigan, K. 2015a A review of rotating cylinder wake transitions. J. Fluids Struct. 53, 2–14; special issue on unsteady separation in fluid-structure interaction – II.Google Scholar
Rao, A., Radi, A., Leontini, J. S., Thompson, M. C., Sheridan, J. & Hourigan, K. 2015b The influence of a small upstream wire on transition in a rotating cylinder wake. J. Fluid Mech. 769, R2-1–R2-12.CrossRefGoogle Scholar
Rao, A., Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2011 Flows past rotating cylinders next to a wall. J. Fluids Struct. 27 (5–6), 668–679.Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2013c The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41 (0), 9–21.Google Scholar
Rao, A., Thompson, M. C. & Hourigan, K. 2016 A universal three-dimensional instability of the wakes of two-dimensional bluff bodies. J. Fluid Mech. 792, 50–66.Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2015c Flow past a rotating cylinder translating at different gap heights along a wall. J. Fluids Struct. 57, 314–330.Google Scholar
Robichaux, J., Balachandar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of a square cylinder. Phys. Fluids 11 (3), 560–578.Google Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 538, 1–29.CrossRefGoogle Scholar
Sheard, G. J. 2007 Cylinders with elliptical cross-section: wake stability with incidence angle variation. In Proceedings of the IUTAM Symposium on Unsteady Separated Flows and Their Control, pp. 5–18. Institut de Mécanique des Fluides de Toulouse.Google Scholar
Sheard, G. J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27 (5–6), 734–742.Google Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004a Asymmetric structure and non-linear transition behaviour of the wakes of toroidal bodies. Eur. J. Mech. (B/Fluids) 23 (1), 167–179.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004b From spheres to circular cylinders: non-axisymmetric transitions in the flow past rings. J. Fluid Mech. 506, 45–78.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2005a Subharmonic mechanism of the mode C instability. Phys. Fluids 17 (11), 1–4.Google Scholar
Sheard, G. J., Thompson, M. C., Hourigan, K. & Leweke, T. 2005b The evolution of a subharmonic mode in a vortex street. J. Fluid Mech. 534, 23–38.Google Scholar
Stewart, B. E., Hourigan, K., Thompson, M. C. & Leweke, T. 2006 Flow dynamics and forces associated with a cylinder rolling along a wall. Phys. Fluids 18 (11), 111701,1–4.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.Google Scholar
Strouhal, V. 1878 Ueber eine besondere art der tonerregung. Annalen der Physik 241 (10), 216–251.Google Scholar
Thompson, M. C. & Hourigan, K. 2003 The sensitivity of steady vortex breakdown bubbles in confined cylinder flows to rotating lid misalignment. J. Fluid Mech. 496, 129–138.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006a Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 1356–1369.Google Scholar
Thompson, M. C., Hourigan, K., Ryan, K. & Sheard, G. J. 2006b Wake transition of two-dimensional cylinders and axisymmetric bluff bodies. J. Fluids Struct. 22, 793–806.CrossRefGoogle Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Thompson, M. C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.Google Scholar
Wei, D. J., Yoon, H. S. & Jung, J. H. 2016 Characteristics of aerodynamic forces exerted on a twisted cylinder at a low Reynolds number of 100. Comput. Fluids 136, 456–466.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.Google Scholar
Williamson, C. H. K. 1992 The natural and forced formation of spot-like in the transition of a wake. J. Fluid Mech. 243, 393–441.Google Scholar
Williamson, C. H. K. 1996a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C. H. K. 1996b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Yang, D., Pettersen, B., Andersson, H. I. & Narasimhamurthy, V. D. 2012 Vortex shedding in flow past an inclined flat plate at high incidence. Phys. Fluids 24 (8), 084103.CrossRefGoogle Scholar
Yang, D., Pettersen, B., Andersson, H. I. & Narasimhamurthy, V. D. 2013 Floquet stability analysis of the wake of an inclined flat plate. Phys. Fluids 25 (9), 094103.Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013a Energy contents and vortex dynamics in Mode-C transition of wired-cylinder wake. Phys. Fluids 25 (5), 054103.Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013b Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.Google Scholar
Yoon, H. S., Yin, J., Choi, C., Balachandar, S. & Ha, M. Y. 2016 Bifurcation of laminar flow around an elliptic cylinder at incidence for low Reynolds numbers. Prog. Comput. Fluid Dyn. 16 (3), 163–178.CrossRefGoogle Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., Konig, M. & Eckelemann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.Google Scholar
Zienkiewicz, O. C. 1977 The Finite Element Method, 3rd edn. McGraw-Hill.Google Scholar