Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Radi, A.
Thompson, M. C.
Rao, A.
Hourigan, K.
and
Sheridan, J.
2013.
Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder.
Journal of Fluid Mechanics,
Vol. 734,
Issue. ,
p.
567.
Bourguet, Rémi
and
Lo Jacono, David
2014.
Flow-induced vibrations of a rotating cylinder.
Journal of Fluid Mechanics,
Vol. 740,
Issue. ,
p.
342.
Navrose,
Meena, Jagmohan
and
Mittal, Sanjay
2015.
Three-dimensional flow past a rotating cylinder.
Journal of Fluid Mechanics,
Vol. 766,
Issue. ,
p.
28.
Leontini, Justin S.
Lo Jacono, David
and
Thompson, Mark C.
2015.
Stability analysis of the elliptic cylinder wake.
Journal of Fluid Mechanics,
Vol. 763,
Issue. ,
p.
302.
Wang, Huakun
Zhao, Dongliang
Yang, Wenyu
and
Yu, Guoliang
2015.
Numerical investigation on flow-induced vibration of a triangular cylinder at a low Reynolds number.
Fluid Dynamics Research,
Vol. 47,
Issue. 1,
p.
015501.
Rao, A.
Thompson, M.C.
Leweke, T.
and
Hourigan, K.
2015.
Flow past a rotating cylinder translating at different gap heights along a wall.
Journal of Fluids and Structures,
Vol. 57,
Issue. ,
p.
314.
Seyed-Aghazadeh, Banafsheh
and
Modarres-Sadeghi, Yahya
2015.
An experimental investigation of vortex-induced vibration of a rotating circular cylinder in the crossflow direction.
Physics of Fluids,
Vol. 27,
Issue. 6,
Rao, A.
Radi, A.
Leontini, J.S.
Thompson, M.C.
Sheridan, J.
and
Hourigan, K.
2015.
A review of rotating cylinder wake transitions.
Journal of Fluids and Structures,
Vol. 53,
Issue. ,
p.
2.
Rao, Anirudh
Radi, Alexander
Leontini, Justin S.
Thompson, Mark C.
Sheridan, John
and
Hourigan, Kerry
2015.
The influence of a small upstream wire on transition in a rotating cylinder wake.
Journal of Fluid Mechanics,
Vol. 769,
Issue. ,
Bourguet, Rémi
and
Lo Jacono, David
2015.
In-line flow-induced vibrations of a rotating cylinder.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
127.
Martín-Alcántara, A.
Sanmiguel-Rojas, E.
and
Fernandez-Feria, R.
2015.
On the development of lift and drag in a rotating and translating cylinder.
Journal of Fluids and Structures,
Vol. 54,
Issue. ,
p.
868.
Afroz, Farhana
Sharif, Muhammad A.R.
and
Lang, Amy
2016.
Numerical study of adverse pressure gradient generation over a flat plate using a rotating cylinder.
Journal of Fluids and Structures,
Vol. 62,
Issue. ,
p.
187.
Rao, Anirudh
Thompson, Mark C.
and
Hourigan, Kerry
2016.
A universal three-dimensional instability of the wakes of two-dimensional bluff bodies.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
50.
Houdroge, F. Y.
Leweke, T.
Hourigan, K.
and
Thompson, M. C.
2017.
Two- and three-dimensional wake transitions of an impulsively started uniformly rolling circular cylinder.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
32.
Rana, Khushbakht
Manzoor, S.
Sheikh, N.A.
Ali, Muzaffar
and
Ali, H.M.
2017.
Gust response of a rotating circular cylinder in the vortex suppression regime.
International Journal of Heat and Mass Transfer,
Vol. 115,
Issue. ,
p.
763.
Naik, Sandeep N.
Vengadesan, S.
and
Prakash, K. Arul
2017.
Numerical study of fluid flow past a rotating elliptic cylinder.
Journal of Fluids and Structures,
Vol. 68,
Issue. ,
p.
15.
Rao, Anirudh
Leontini, Justin S.
Thompson, Mark C.
and
Hourigan, Kerry
2017.
Three-dimensionality of elliptical cylinder wakes at low angles of incidence.
Journal of Fluid Mechanics,
Vol. 825,
Issue. ,
p.
245.
Afroz, Farhana
and
Sharif, Muhammad A R
2018.
Numerical analysis of the flow separation and adverse pressure gradient in laminar boundary layer over a flat plate due to a rotating cylinder in the vicinity.
Fluid Dynamics Research,
Vol. 50,
Issue. 2,
p.
025501.
Lu, H.
Lua, K.B.
and
Lim, T.T.
2018.
Flow past a rapidly rotating elliptic cylinder.
European Journal of Mechanics - B/Fluids,
Vol. 72,
Issue. ,
p.
676.
Lo Jacono, David
Bourguet, Rémi
Thompson, Mark C.
and
Leontini, Justin S.
2018.
Three-dimensional mode selection of the flow past a rotating and inline oscillating cylinder.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
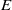 $E$) appears consistent with a hyperbolic instability in the wake, while the second (named mode
$E$) appears consistent with a hyperbolic instability in the wake, while the second (named mode 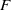 $F$) appears to be a centrifugal instability of the flow very close to the cylinder surface. At higher rotation rates on the second steady state, a single three-dimensional mode due to centrifugal instability (named mode
$F$) appears to be a centrifugal instability of the flow very close to the cylinder surface. At higher rotation rates on the second steady state, a single three-dimensional mode due to centrifugal instability (named mode 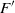 ${F}^{\prime } $) is found. This mode becomes increasingly difficult to excite as the rotation rate is increased.
${F}^{\prime } $) is found. This mode becomes increasingly difficult to excite as the rotation rate is increased.