Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Peng, Si
Wang, Hanfeng
Zeng, Lingwei
and
He, Xuhui
2019.
Low-frequency dynamics of the flow around a finite-length square cylinder.
Experimental Thermal and Fluid Science,
Vol. 109,
Issue. ,
p.
109877.
Tanweer, Sartaj
Dewan, Anupam
and
Sanghi, Sanjeev
2020.
Influence of three-dimensional wake transition on heat transfer from a square cylinder near a moving wall.
International Journal of Heat and Mass Transfer,
Vol. 148,
Issue. ,
p.
118986.
Xiang, Gong
and
Guedes Soares, C.
2020.
Improved dynamical modelling of freely falling underwater cylinder based on CFD.
Ocean Engineering,
Vol. 211,
Issue. ,
p.
107538.
Sun, Xu
Steve Suh, C.
Sun, Chaochao
and
Yu, Bo
2021.
Vortex-induced vibration of a flexible splitter plate attached to a square cylinder in laminar flow.
Journal of Fluids and Structures,
Vol. 101,
Issue. ,
p.
103206.
Devi, Kalpana
Hanmaiahgari, Prashanth Reddy
Balachandar, Ram
and
Pu, Jaan H.
2021.
A Comparative Study between Sand- and Gravel-Bed Open Channel Flows in the Wake Region of a Bed-Mounted Horizontal Cylinder.
Fluids,
Vol. 6,
Issue. 7,
p.
239.
Agbaglah, G. Gilou
2021.
Numerical study of hole formation in a thin flapping liquid sheet sheared by a fast gas stream.
Physics of Fluids,
Vol. 33,
Issue. 6,
Vadsola, M.
Agbaglah, G. G.
and
Mavriplis, C.
2021.
Slat cove dynamics of low Reynolds number flow past a 30P30N high lift configuration.
Physics of Fluids,
Vol. 33,
Issue. 3,
Tanweer, Sartaj
Dewan, Anupam
and
Sanghi, Sanjeev
2022.
Flow dynamics in the wake of a rectangular cylinder near a moving wall.
Ocean Engineering,
Vol. 266,
Issue. ,
p.
112966.
Liu, Hao
Qu, Yegao
Xie, Fangtao
and
Meng, Guang
2022.
Vortex-induced vibration of large deformable underwater composite beams based on a nonlinear higher-order shear deformation zig-zag theory.
Ocean Engineering,
Vol. 250,
Issue. ,
p.
111000.
Lin, L M
2022.
Initially generated pure mode A in the three-dimensional wake transition of a circular cylinder.
Fluid Dynamics Research,
Vol. 54,
Issue. 3,
p.
035504.
Li, Ming
Li, Qiusheng
Shi, Haoyun
and
Li, Mingshui
2022.
Effects of free-stream turbulence on the near wake flow and aerodynamic forces of a square cylinder.
Journal of Fluids and Structures,
Vol. 114,
Issue. ,
p.
103748.
Lin, L M
and
Tan, Z R
2022.
DNS of the spatiotemporal evolution of the vorticity in (pure) mode B of a circular cylinder’s wake.
Fluid Dynamics Research,
Vol. 54,
Issue. 1,
p.
015511.
Farrokhi Derakhshandeh, Javad
2022.
Fluid structural interaction of a flexible plate submerged in the wake of a circular cylinder.
Ocean Engineering,
Vol. 266,
Issue. ,
p.
112933.
Feng, Y.L.
Chen, D.Y.
Li, S.W.
Xiao, Q.
and
Li, W.
2022.
Vortex-induced vibrations of flexible cylinders predicted by wake oscillator model with random components of mean drag coefficient and lift coefficient.
Ocean Engineering,
Vol. 251,
Issue. ,
p.
110960.
Kokash, Hussein
and
Agbaglah, G. Gilou
2022.
On the origin of mode B instability of the wake of a square cylinder.
Physics of Fluids,
Vol. 34,
Issue. 7,
Tian, Zhongchu
and
Liao, Zhangying
2023.
Three-Dimensional Numerical Simulation of the Water Flow Effect on a Temporary Pier with Three Columns in Series.
Applied Sciences,
Vol. 13,
Issue. 21,
p.
11683.
Lu, Jiachen
Nazarian, Negin
Hart, Melissa Anne
Krayenhoff, E. Scott
and
Martilli, Alberto
2023.
Novel Geometric Parameters for Assessing Flow Over Realistic Versus Idealized Urban Arrays.
Journal of Advances in Modeling Earth Systems,
Vol. 15,
Issue. 7,
Lin, L M
2023.
Phase transition between pure modes A and B in a circular cylinder’s wake. Part I: analysis of fluid forces.
Fluid Dynamics Research,
Vol. 55,
Issue. 3,
p.
035502.
Wang, Jie
Zhou, Bo
Xu, Haoyuan
Liu, Zhengyuan
Han, Xiaoshuang
and
Zhang, Guiyong
2023.
Wake control of a square cylinder: Impinging the vortex cores with dual flexible splitter plates.
Journal of Fluids and Structures,
Vol. 120,
Issue. ,
p.
103921.
Pawar, Ashish P.
Sarkar, Sandip
and
Saha, Sandip K.
2023.
Three-dimensional study of flow past blunt headed cylinder at low Reynolds numbers.
International Journal of Thermal Sciences,
Vol. 189,
Issue. ,
p.
108256.
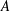 $A$ and
$A$ and 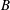 $B$, respectively, and that of the square’s circumscribed circular cylinder are examined by using three-dimensional Navier–Stokes numerical simulations. At small times, prior to the streamwise vortex shedding, a self-similar velocity is observed in the wake and no significant difference is observed in the dynamics of the flows past the square and the circular cylinders. The exponential growth of the three-dimensional instability reaches a saturation regime during this early time for the considered Reynolds numbers. Vortical structures in the wake at long times and shedding frequencies are very close for the square and the circular cylinders. The flow separation on the forward top and bottom corners of the square cylinder have the effect of increasing its effective width, making it comparable with the diameter of the circumscribed circular cylinder. Thus, Floquet multipliers and modes of the associated three-dimensional instabilities are shown to be very close for the two cylinders when using the circumscribed circular cylinder as the basis for a characteristic length scale. Most importantly, the wavenumber with the maximum growth rate, for modes
$B$, respectively, and that of the square’s circumscribed circular cylinder are examined by using three-dimensional Navier–Stokes numerical simulations. At small times, prior to the streamwise vortex shedding, a self-similar velocity is observed in the wake and no significant difference is observed in the dynamics of the flows past the square and the circular cylinders. The exponential growth of the three-dimensional instability reaches a saturation regime during this early time for the considered Reynolds numbers. Vortical structures in the wake at long times and shedding frequencies are very close for the square and the circular cylinders. The flow separation on the forward top and bottom corners of the square cylinder have the effect of increasing its effective width, making it comparable with the diameter of the circumscribed circular cylinder. Thus, Floquet multipliers and modes of the associated three-dimensional instabilities are shown to be very close for the two cylinders when using the circumscribed circular cylinder as the basis for a characteristic length scale. Most importantly, the wavenumber with the maximum growth rate, for modes 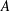 $A$ and
$A$ and 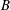 $B$, is approximately identical for the two cylinders.
$B$, is approximately identical for the two cylinders.