Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-07T20:07:33.365Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional wake transition for a circular cylinder near a moving wall

Published online by Cambridge University Press:  05 April 2017

Hongyi Jiang Open the ORCID record for Hongyi Jiang [Opens in a new window] ,
Liang Cheng ,
Scott Draper  and
Hongwei An
Hongyi Jiang
Affiliation:
DUT-UWA Joint Research Centre, State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, 116024, China School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Liang Cheng*
Affiliation:
DUT-UWA Joint Research Centre, State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, 116024, China School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Scott Draper
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia Centre for Offshore Foundation Systems, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Hongwei An
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

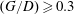Three-dimensional (3D) wake transition for a circular cylinder placed near to a moving wall is investigated using direct numerical simulation (DNS). The study covers a parameter space spanning a gap ratio $(G/D)\geqslant 0.3$ and Reynolds number (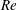$Re$) up to 325. The wake transition regimes in the parameter space are mapped out. It is found that vortex dislocation associated with Mode A is completely suppressed at 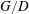$G/D$ smaller than approximately 1.0. The suppression of vortex dislocation is believed to be due to the confinement of the Mode A streamwise vortices by the plane wall, which suppresses the excess growth and local dislocation of any Mode A vortex loop. Detailed wake transition is examined at 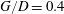$G/D=0.4$, where the wake transition sequence is ‘two-dimensional (2D) $\rightarrow$ ordered Mode A $\rightarrow$ mode swapping (without dislocations) $\rightarrow$ Mode B’. Relatively strong three-dimensionality is found at 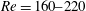$Re=160{-}220$ as the wake is dominated by large-scale structure of ordered Mode A, and also at 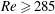$Re\geqslant 285$, where Mode B becomes increasingly disordered. A local reduction in three-dimensionality is observed at 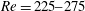$Re=225{-}275$, where the wake is dominated by finer-scale structure of a mixture of ordered Modes A and B. Corresponding variations in the vortex shedding frequency and hydrodynamic forces are also investigated.

JFM classification

Vortex Flows: Vortex instability Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 260 - 287
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bearman, P. W. & Zdravkovich, M. M. 1978 Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 89, 33–47.CrossRefGoogle Scholar
Grass, A. J., Raven, P. W. J., Stuart, R. J. & Bray, J. A. 1984 The influence of boundary layer velocity gradients and bed proximity on vortex shedding from free spanning pipelines. J. Energy Resour. Technol. 106, 70–78.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Huang, W. X. & Sung, H. J. 2007 Vortex shedding from a circular cylinder near a moving wall. J. Fluids Struct. 23, 1064–1076.Google Scholar
Issa, R. I. 1986 Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017 Two- and three-dimensional instabilities in the wake of a circular cylinder near a moving wall. J. Fluid Mech. 812, 435–462.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016 Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.CrossRefGoogle Scholar
Lei, C., Cheng, L., Armfield, S. W. & Kavanagh, K. 2000 Vortex shedding suppression for flow over a circular cylinder near a plane boundary. Ocean Engng 27, 1109–1127.Google Scholar
Lei, C., Cheng, L. & Kavanagh, K. 1999 Re-examination of the effect of a plane boundary on force and vortex shedding of a circular cylinder. J. Wind Engng Ind. Aerodyn. 80, 263–286.CrossRefGoogle Scholar
Leweke, T. & Williamson, C. H. K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.CrossRefGoogle Scholar
Price, S. J., Sumner, D., Smith, J. G., Leong, K. & Païdoussis, M. P. 2002 Flow visualization around a circular cylinder near to a plane wall. J. Fluids Struct. 16, 175–191.Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2013 The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41, 9–21.Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2015 Flow past a rotating cylinder translating at different gap heights along a wall. J. Fluids Struct. 57, 314–330.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.Google Scholar
Taneda, S. 1965 Experimental investigation of vortex streets. J. Phys. Soc. Japan 20, 1714–1721.CrossRefGoogle Scholar
Thapa, J., Zhao, M., Zhou, T. & Cheng, L. 2014 Three-dimensional simulation of vortex shedding flow in the wake of a yawed circular cylinder near a plane boundary at a Reynolds number of 500. Ocean Engng 87, 25–39.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.Google Scholar
Wang, X. K. & Tan, S. K. 2008 Near-wake flow characteristics of a circular cylinder close to a wall. J. Fluids Struct. 24, 605–627.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Yoon, H. S., Lee, J. B., Seo, J. H. & Park, H. S. 2010 Characteristics for flow and heat transfer around a circular cylinder near a moving wall in wide range of low Reynolds number. Intl J. Heat Mass Transfer 53, 5111–5120.CrossRefGoogle Scholar
Zdravkovich, M. M. 1985 Observation of vortex shedding behind a towed circular cylinder near a wall. In Proceedings of the 3rd International Symposium on Flow Visualization, Ann Arbor, Michigan, pp. 423–427. Hemisphere Publishing Corp.Google Scholar