Article contents
Three-dimensional vorticity, momentum and heat transport in a turbulent cylinder wake
Published online by Cambridge University Press: 09 November 2016
Abstract
The transport of momentum and heat in the turbulent intermediate wake of a circular cylinder is inherently three-dimensional (3-D). This work aims to gain new insight into the 3-D vorticity structure, momentum and heat transport in this flow. All three components of the velocity and vorticity vectors, along with the fluctuating temperature, are measured simultaneously, at nominally the same point in the flow, with a probe consisting of four X-wires and four cold wires. Measurements are made in the ( $x$,
$x$, 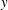 $y$) or mean shear plane at
$y$) or mean shear plane at 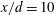 $x/d=10$, 20 and 40 at a Reynolds number of
$x/d=10$, 20 and 40 at a Reynolds number of 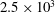 $2.5\times 10^{3}$ based on the cylinder diameter
$2.5\times 10^{3}$ based on the cylinder diameter  $d$ and the free-stream velocity. A phase-averaging technique is developed to separate the large-scale coherent structures from the remainder of the flow. It is found that the effects of vorticity on heat transport at
$d$ and the free-stream velocity. A phase-averaging technique is developed to separate the large-scale coherent structures from the remainder of the flow. It is found that the effects of vorticity on heat transport at 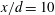 $x/d=10$ and
$x/d=10$ and 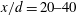 $x/d=20{-}40$ are distinctly different. At
$x/d=20{-}40$ are distinctly different. At 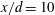 $x/d=10$, both spanwise and streamwise vorticity components account significantly for the heat flux. At
$x/d=10$, both spanwise and streamwise vorticity components account significantly for the heat flux. At 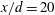 $x/d=20$ and 40, the spanwise vortex rollers play a major role in inducing the coherent components of the heat flux vector, while the ribs are responsible for the small-scale heat diffusion out of the spanwise vortex rollers. The present data indicate that, if the spanwise-velocity-related terms are ignored, the estimated values of the production can have errors of approximately 22 % and 13 % respectively for the turbulent energy and temperature variance at
$x/d=20$ and 40, the spanwise vortex rollers play a major role in inducing the coherent components of the heat flux vector, while the ribs are responsible for the small-scale heat diffusion out of the spanwise vortex rollers. The present data indicate that, if the spanwise-velocity-related terms are ignored, the estimated values of the production can have errors of approximately 22 % and 13 % respectively for the turbulent energy and temperature variance at 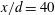 $x/d=40$, and the errors are expected to further increase downstream. A conceptual model summarizing the 3-D features of the heat and momentum transports at
$x/d=40$, and the errors are expected to further increase downstream. A conceptual model summarizing the 3-D features of the heat and momentum transports at 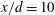 $x/d=10$ is proposed. Compared with the previous two-dimensional model of Matsumura & Antonia (J. Fluid Mech., vol. 250, 1993, pp. 651–668) or MA, the new model provides a more detailed description of the role the rib-like structures undertake in transporting heat and momentum, and also underlines the importance of the upstream half of the spanwise vortex rollers, instead of only one quadrant of these rollers, as in the MA model, in diffusing heat out of the vortex.
$x/d=10$ is proposed. Compared with the previous two-dimensional model of Matsumura & Antonia (J. Fluid Mech., vol. 250, 1993, pp. 651–668) or MA, the new model provides a more detailed description of the role the rib-like structures undertake in transporting heat and momentum, and also underlines the importance of the upstream half of the spanwise vortex rollers, instead of only one quadrant of these rollers, as in the MA model, in diffusing heat out of the vortex.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 19
- Cited by



