Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T19:43:47.464Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional organisation of primary and secondary crossflow instability

Published online by Cambridge University Press:  21 June 2016

Jacopo Serpieri  and
Marios Kotsonis
Jacopo Serpieri*
Affiliation:
AWEP Department, Section of Aerodynamics, Delft University of Technology, Kluyverweg 1, 2629HS Delft, The Netherlands
Marios Kotsonis
Affiliation:
AWEP Department, Section of Aerodynamics, Delft University of Technology, Kluyverweg 1, 2629HS Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An experimental investigation of primary and secondary crossflow instability developing in the boundary layer of a 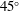$45^{\circ }$ swept wing at a chord Reynolds number of 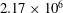$2.17\times 10^{6}$ is presented. Linear stability theory is applied for preliminary estimation of the flow stability while surface flow visualisation using fluorescent oil is employed to inspect the topological features of the transition region. Hot-wire anemometry is extensively used for the investigation of the developing boundary layer and identification of the statistical and spectral characteristics of the instability modes. Primary stationary, as well as unsteady type-I (z-mode), type-II (y-mode) and type-III modes are detected and quantified. Finally, three-component, three-dimensional measurements of the transitional boundary layer are performed using tomographic particle image velocimetry. This research presents the first application of an optical experimental technique for this type of flow. Among the optical techniques, tomographic velocimetry represents, to date, the most advanced approach allowing the investigation of spatially correlated flow structures in three-dimensional fields. Proper orthogonal decomposition (POD) analysis of the captured flow fields is applied to this goal. The first POD mode features a newly reported structure related to low-frequency oscillatory motion of the stationary vortices along the spanwise direction. The cause of this phenomenon is only conjectured. Its effect on transition is considered negligible but, given the related high energy level, it needs to be accounted for in experimental investigations. Secondary instability mechanisms are captured as well. The type-III mode corresponds to low-frequency primary travelling crossflow waves interacting with the stationary ones. It appears in the inner upwelling region of the stationary crossflow vortices and is characterised by elongated structures approximately aligned with the axis of the stationary waves. The type-I secondary instability consists instead of significantly inclined structures located at the outer upwelling region of the stationary vortices. The much narrower wavelength and higher advection velocity of these structures correlate with the higher-frequency content of this mode. The results of the investigation of both primary and secondary instability from the exploited techniques agree with and complement each other and are in line with existing literature. Finally, they present the first experimental observation of the secondary instability structures under natural flow conditions.

JFM classification

Boundary Layers: Boundary layer stability Boundary Layers: Boundary layer structure
Type
Papers
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , pp. 200 - 245
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Arnal, D. & Casalis, G. 2000 Laminar-turbulent transition prediction in three-dimensional flows. Prog. Aerosp. Sci. 36 (2), 173–191.CrossRefGoogle Scholar
Arnal, D., Gasparian, G. & Salinas, H.1998 Recent advances in theoretical methods for laminar-turbulent transition prediction. AIAA Paper 1998-0223.CrossRefGoogle Scholar
Bippes, H. 1999 Basic experiments on transition in three-dimensional boundary layers dominated by crossflow instability. Prog. Aerosp. Sci. 35 (4), 363–412.CrossRefGoogle Scholar
Bonfigli, G. & Kloker, M. 2007 Secondary instability of crossflow vortices: validation of the stability theory by direct numerical simulation. J. Fluid Mech. 583, 229–272.CrossRefGoogle Scholar
Bridges, T. J. & Morris, P. J. 1984 Differential eigenvalue problems in which the parameter appears nonlinearly. J. Comput. Phys. 55 (3), 437–460.CrossRefGoogle Scholar
Chernoray, V. G., Dovgal, A. V., Kozlov, V. V. & Löfdahl, L. 2005 Experiments on secondary instability of streamwise vortices in a swept-wing boundary layer. J. Fluid Mech. 534, 295–325.CrossRefGoogle Scholar
Dagenhart, J. R., Saric, W. S., Mousseux, M. C. & Stack, J. P.1989 Crossflow vortex instability and transition on a 45-degree swept wing. AIAA Paper 89-1982.CrossRefGoogle Scholar
Deyhle, H. & Bippes, H. 1996 Disturbance growth in an unstable three-dimensional boundary layer and its dependence on environmental conditions. J. Fluid Mech. 316, 73–113.CrossRefGoogle Scholar
Downs, R. S. III & White, E. B. 2013 Free-stream turbulence and the development of cross-flow disturbances. J. Fluid Mech. 735, 347–380.CrossRefGoogle Scholar
Elsinga, G. E., Scarano, F., Wieneke, B. & van Oudheusden, B. W. 2006 Tomographic particle image velocimetry. Exp. Fluids 41 (6), 933–947.CrossRefGoogle Scholar
Fischer, T. M. & Dallmann, U. 1991 Primary and secondary stability analysis of a three-dimensional boundary-layer flow. Phys. Fluids A 3 (10), 2378–2391.CrossRefGoogle Scholar
Glauser, M. N., Saric, W. S., Chapman, K. L. & Reibert, M. S. 2014 Swept-wing boundary-layer transition and turbulent flow physics from multipoint measurements. AIAA J. 52 (2), 338–347.CrossRefGoogle Scholar
Haynes, T. S. & Reed, H. L. 2000 Simulation of swept-wing vortices using nonlinear parabolized stability equations. J. Fluid Mech. 405, 325–349.CrossRefGoogle Scholar
Högberg, M. & Henningson, D. 1998 Secondary instability of cross-flow vortices in Falkner–Skan–Cooke boundary layers. J. Fluid Mech. 368, 339–357.CrossRefGoogle Scholar
Hosseini, S. M., Tempelmann, D., Hanifi, A. & Henningson, D. S. 2013 Stabilization of a swept-wing boundary layer by distributed roughness elements. J. Fluid Mech. 718, R1.CrossRefGoogle Scholar
Janke, E. & Balakumar, P. 2000 On the secondary instability of three-dimensional boundary layers. Theor. Comput. Fluid Dyn. 14 (3), 167–194.CrossRefGoogle Scholar
Kawakami, M., Kohama, Y. & Okutsu, M.1999 Stability characteristics of stationary crossflow vortices in three-dimensional boundary layer. AIAA Paper 1998-811.CrossRefGoogle Scholar
Koch, W. 2002 On the spatio-temporal stability of primary and secondary crossflow vortices in a three-dimensional boundary layer. J. Fluid Mech. 456, 85–111.CrossRefGoogle Scholar
Koch, W., Bertolotti, F. P., Stolte, A. & Hein, S. 2000 Nonlinear equilibrium solutions in a three-dimensional boundary layer and their secondary instability. J. Fluid Mech. 406, 131–174.CrossRefGoogle Scholar
Kohama, Y., Saric, W. S. & Hoos, J. A. 1991 A high frequency secondary instability of crossflow vortices that leads to transition. In Proc. R. Aeronaut. Soc. Conf. on Boundary-Layer Transition and Control, Cambridge, UK.Google Scholar
Kurz, H. B. E. & Kloker, M. J. 2014 Receptivity of a swept-wing boundary layer to micron-sized discrete roughness elements. J. Fluid Mech. 755, 62–82.CrossRefGoogle Scholar
Lingwood, R. J. 1997 On the impulse response for swept boundary-layer flows. J. Fluid Mech. 344, 317–334.CrossRefGoogle Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 166–178. Nauka.Google Scholar
Lynch, K. P. & Scarano, F. 2014 Experimental determination of tomographic piv accuracy by a 12-camera system. Meas. Sci. Technol. 25 (8), 084003.CrossRefGoogle Scholar
Mack, L. M.1984 Boundary-layer linear stability theory AGARD Report 709.Google Scholar
Malik, M. R., Li, F. & Chang, C.-L. 1994 Crossflow disturbances in three-dimensional boundary layers: nonlinear development, wave interaction and secondary instability. J. Fluid Mech. 268, 1–36.CrossRefGoogle Scholar
Malik, M. R., Li, F., Choudhari, M. & Chang, C.-L. 1999 Secondary instability of crossflow vortices and swept-wing boundary-layer transition. J. Fluid Mech. 399, 85–115.CrossRefGoogle Scholar
Nati, G., Kotsonis, M., Ghaemi, S. & Scarano, F. 2013 Control of vortex shedding from a blunt trailing edge using plasma actuators. Exp. Therm. Fluid Sci. 46, 199–210.CrossRefGoogle Scholar
Poll, D. I. A. 1985 Some observations of the transition process on the windward face of a long yawed cylinder. J. Fluid Mech. 150, 329–356.CrossRefGoogle Scholar
Radeztsky, R. H., Reibert, M. S. & Saric, W. S. 1999 Effect of isolated micron-sized roughness on transition in swept-wing flows. AIAA J. 37 (11), 1370–1377.CrossRefGoogle Scholar
Raiola, M., Discetti, S. & Ianiro, A. 2015 On piv random error minimization with optimal pod-based low-order reconstruction. Exp. Fluids 56 (4), 1–15.CrossRefGoogle Scholar
Reibert, M. S., Saric, W. S., Carrillo, R. B. Jr. & Chapman, K.1996 Experiments in nonlinear saturation of stationary crossflow vortices in a swept-wing boundary layer. AIAA Paper 1996-0184.CrossRefGoogle Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1996 Hot-wire anemometry behaviour at very high frequencies. Meas. Sci. Technol. 7 (10), 1297–1300.CrossRefGoogle Scholar
Saric, W., Carrillo, R. Jr. & Reibert, M. 1998 Leading-edge roughness as a transition control mechanism. AIAA Paper 1998-781.CrossRefGoogle Scholar
Saric, W. S., Carpenter, A. L. & Reed, H. L. 2011 Passive control of transition in three-dimensional boundary layers, with emphasis on discrete roughness elements. Phil. Trans. R. Soc. Lond. A 369 (1940), 1352–1364.Google ScholarPubMed
Saric, W. S., Reed, H. L. & White, E. B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35 (1), 413–440.CrossRefGoogle Scholar
Scarano, F. 2002 Iterative image deformation methods in piv. Meas. Sci. Technol. 13 (1), R1–R19.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory. Cambridge University Press.CrossRefGoogle Scholar
Serpieri, J. & Kotsonis, M.2015a Design of a swept wing wind tunnel model for study of cross-flow instability. AIAA Paper 2015-2576.CrossRefGoogle Scholar
Serpieri, J. & Kotsonis, M. 2015b Flow visualization of the boundary layer transition pattern on a swept wing. In 10th Pacific Symposium on Flow Visualization and Image Processing, Naples, Italy.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part i: coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Tempelmann, D., Schrader, L.-U., Hanifi, A., Brandt, L. & Henningson, D. S. 2012 Swept wing boundary-layer receptivity to localized surface roughness. J. Fluid Mech. 711, 516–544.CrossRefGoogle Scholar
Van Oudheusden, B. W., Scarano, F., Van Hinsberg, N. P. & Watt, D. W. 2005 Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 39 (1), 86–98.CrossRefGoogle Scholar
Violato, D. & Scarano, F. 2013 Three-dimensional vortex analysis and aeroacoustic source characterization of jet core breakdown. Phys. Fluids 25 (1), 015112.CrossRefGoogle Scholar
Wassermann, P. & Kloker, M. 2002 Mechanisms and passive control of crossflow-vortex-induced transition in a three-dimensional boundary layer. J. Fluid Mech. 456, 49–84.CrossRefGoogle Scholar
Wassermann, P. & Kloker, M. 2003 Transition mechanisms induced by travelling crossflow vortices in a three-dimensional boundary layer. J. Fluid Mech. 483, 67–89.CrossRefGoogle Scholar
Welch, P. D. 1967 The use of fast fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15 (2), 70–73.CrossRefGoogle Scholar
White, E. & Saric, W.2000 Application of variable leading-edge roughness for transition control on swept wings. AIAA Paper 2000-283.CrossRefGoogle Scholar
White, E. B. & Saric, W. S. 2005 Secondary instability of crossflow vortices. J. Fluid Mech. 525, 275–308.CrossRefGoogle Scholar
Wieneke, B. 2008 Volume self-calibration for 3d particle image velocimetry. Exp. Fluids 45 (4), 549–556.CrossRefGoogle Scholar

Serpieri and Kotsonis supplementary movies

Reconstructed POD mode 1 from the measured time coefficients (f=0.5Hz)

Download Serpieri and Kotsonis supplementary movies(Video)
Video 2.2 MB

Serpieri and Kotsonis supplementary movies

Reconstructed type-III secondary instability based on the estimated frequency (f=500Hz)

Download Serpieri and Kotsonis supplementary movies(Video)
Video 2.7 MB

Serpieri and Kotsonis supplementary movies

Reconstructed type-I secondary instability based on the estimated frequency (f=5000Hz)

Download Serpieri and Kotsonis supplementary movies(Video)
Video 2.7 MB