Article contents
Three-dimensional buoyancy-driven flow along a fractured boundary
Published online by Cambridge University Press: 09 July 2013
Abstract
We describe the steady motion of a buoyant fluid migrating through a porous layer along a plane, inclined boundary from a localized well. We first describe the transition from an approximately radially spreading current near the source, to a flow which runs upslope, as it spreads in the cross-slope direction. Using the model, we predict the maximum injection rate for which, near the source, the flow does not fully flood the porous layer. We then account for the presence of a fracture on the boundary through which some of the flow can drain upwards, and calculate how the current is partitioned between the fraction that drains and the remainder which continues running upslope. The fraction that drains increases with the permeability of the fracture and also with the distance from the source, as the flow slows and has more time to drain. We introduce new scalings and some asymptotic solutions to describe both the flow near the fracture and the three-dimensional surface of the injected fluid as it spreads upslope. We extend the model to the case of multiple fractures, so that the current eventually drains away as it flows over successive fractures. We calculate the shape of the region that is invaded by the buoyant fluid and we show that this flow, draining through a series of discrete fractures, may be approximated by a flow that continuously drains through its upper boundary. The effective small uniform permeability of this upper boundary is given by 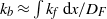 ${k}_{b} \approx \int \nolimits {k}_{f} \hspace{0.167em} \mathrm{d} x/ {D}_{F} $, where
${k}_{b} \approx \int \nolimits {k}_{f} \hspace{0.167em} \mathrm{d} x/ {D}_{F} $, where 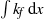 $\int \nolimits {k}_{f} \hspace{0.167em} \mathrm{d} x$ is the integral of permeability across the width of the fracture and
$\int \nolimits {k}_{f} \hspace{0.167em} \mathrm{d} x$ is the integral of permeability across the width of the fracture and 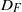 ${D}_{F} $ is the inter-fracture spacing. Finally, we discuss the relevance of the work for CO2 sequestration and we compare some simple predictions of the plume shape, volume and volume flux derived from our model with data from the Sleipner project, Norway for the plume of CO2 which developed in Horizon 1.
${D}_{F} $ is the inter-fracture spacing. Finally, we discuss the relevance of the work for CO2 sequestration and we compare some simple predictions of the plume shape, volume and volume flux derived from our model with data from the Sleipner project, Norway for the plume of CO2 which developed in Horizon 1.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 5
- Cited by


