Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wagner, G. L.
Ferrando, G.
and
Young, W. R.
2017.
An asymptotic model for the propagation of oceanic internal tides through quasi-geostrophic flow.
Journal of Fluid Mechanics,
Vol. 828,
Issue. ,
p.
779.
Thomas, Jim
2017.
New model for acoustic waves propagating through a vortical flow.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
658.
Meroni, Agostino N.
Miller, Madeline D.
Tziperman, Eli
and
Pasquero, Claudia
2017.
Nonlinear Energy Transfer among Ocean Internal Waves in the Wake of a Moving Cyclone.
Journal of Physical Oceanography,
Vol. 47,
Issue. 8,
p.
1961.
Thomas, Jim
Smith, K. Shafer
and
Bühler, Oliver
2017.
Near-inertial wave dispersion by geostrophic flows.
Journal of Fluid Mechanics,
Vol. 817,
Issue. ,
p.
406.
Achatz, U.
Ribstein, B.
Senf, F.
and
Klein, R.
2017.
The interaction between synoptic‐scale balanced flow and a finite‐amplitude mesoscale wave field throughout all atmospheric layers: weak and moderately strong stratification.
Quarterly Journal of the Royal Meteorological Society,
Vol. 143,
Issue. 702,
p.
342.
Barkan, Roy
Winters, Kraig B.
and
McWilliams, James C.
2017.
Stimulated Imbalance and the Enhancement of Eddy Kinetic Energy Dissipation by Internal Waves.
Journal of Physical Oceanography,
Vol. 47,
Issue. 1,
p.
181.
Thomas, Leif N.
2017.
On the modifications of near-inertial waves at fronts: implications for energy transfer across scales.
Ocean Dynamics,
Vol. 67,
Issue. 10,
p.
1335.
Dunphy, Michael
Ponte, Aurélien L.
Klein, Patrice
and
Le Gentil, Sylvie
2017.
Low-Mode Internal Tide Propagation in a Turbulent Eddy Field.
Journal of Physical Oceanography,
Vol. 47,
Issue. 3,
p.
649.
Grooms, Ian
and
Julien, Keith
2018.
Multiscale Models in Geophysical Fluid Dynamics.
Earth and Space Science,
Vol. 5,
Issue. 11,
p.
668.
Fan, Boyu
Kataoka, T.
and
Akylas, T. R.
2018.
On the interaction of an internal wavepacket with its induced mean flow and the role of streaming.
Journal of Fluid Mechanics,
Vol. 838,
Issue. ,
Thomas, Jim
Bühler, Oliver
and
Shafer Smith, K.
2018.
Wave-induced mean flows in rotating shallow water with uniform potential vorticity.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
p.
408.
Rocha, Cesar B.
Wagner, Gregory L.
and
Young, William R.
2018.
Stimulated generation: extraction of energy from balanced flow by near-inertial waves.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
417.
Thomas, Jim
and
Yamada, Ray
2018.
An amplitude equation for surface gravity wave-topography interactions.
Physical Review Fluids,
Vol. 3,
Issue. 12,
Jing, Zhao
Chang, Ping
DiMarco, S. F.
and
Wu, Lixin
2018.
Observed Energy Exchange between Low-Frequency Flows and Internal Waves in the Gulf of Mexico.
Journal of Physical Oceanography,
Vol. 48,
Issue. 4,
p.
995.
Savva, Miles A. C.
and
Vanneste, Jacques
2018.
Scattering of internal tides by barotropic quasigeostrophic flows.
Journal of Fluid Mechanics,
Vol. 856,
Issue. ,
p.
504.
van den Bremer, T. S.
Yassin, H.
and
Sutherland, B. R.
2019.
Lagrangian transport by vertically confined internal gravity wavepackets.
Journal of Fluid Mechanics,
Vol. 864,
Issue. ,
p.
348.
Asselin, Olivier
and
Young, William R.
2019.
An improved model of near-inertial wave dynamics.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
428.
Thomas, Jim
and
Yamada, Ray
2019.
Geophysical turbulence dominated by inertia–gravity waves.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
71.
Li, Qiang
Mao, Xianzhong
Huthnance, John
Cai, Shuqun
and
Kelly, Samuel
2019.
On Internal Waves Propagating across a Geostrophic Front.
Journal of Physical Oceanography,
Vol. 49,
Issue. 5,
p.
1229.
Sutherland, Bruce R.
Achatz, Ulrich
Caulfield, Colm-cille P.
and
Klymak, Jody M.
2019.
Recent progress in modeling imbalance in the atmosphere and ocean.
Physical Review Fluids,
Vol. 4,
Issue. 1,
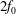 $2f_{0}$, where
$2f_{0}$, where 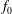 $f_{0}$ is the local inertial frequency. This ‘three-component’ model extends the two-component model derived by Xie & Vanneste (J. Fluid Mech., vol. 774, 2015, pp. 143–169) to include interactions between near-inertial and
$f_{0}$ is the local inertial frequency. This ‘three-component’ model extends the two-component model derived by Xie & Vanneste (J. Fluid Mech., vol. 774, 2015, pp. 143–169) to include interactions between near-inertial and 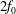 $2f_{0}$ waves. Both models possess two conservation laws which together imply that oceanic NIWs forced by winds, tides or flow over bathymetry can extract energy from quasi-geostrophic flows. A second and separate implication of the three-component model is that quasi-geostrophic flow catalyses a loss of NIW energy to freely propagating waves with near-
$2f_{0}$ waves. Both models possess two conservation laws which together imply that oceanic NIWs forced by winds, tides or flow over bathymetry can extract energy from quasi-geostrophic flows. A second and separate implication of the three-component model is that quasi-geostrophic flow catalyses a loss of NIW energy to freely propagating waves with near-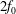 $2f_{0}$ frequency that propagate rapidly to depth and transfer energy back to the NIW field at very small vertical scales. The upshot of near-
$2f_{0}$ frequency that propagate rapidly to depth and transfer energy back to the NIW field at very small vertical scales. The upshot of near-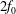 $2f_{0}$ generation is a two-step mechanism whereby quasi-geostrophic flow catalyses a nonlinear transfer of near-inertial energy to the small scales of wave breaking and diapycnal mixing. A comparison of numerical solutions with both Boussinesq and three-component models for a two-dimensional initial value problem reveals strengths and weaknesses of the model while demonstrating the extraction of quasi-geostrophic energy and production of small vertical scales.
$2f_{0}$ generation is a two-step mechanism whereby quasi-geostrophic flow catalyses a nonlinear transfer of near-inertial energy to the small scales of wave breaking and diapycnal mixing. A comparison of numerical solutions with both Boussinesq and three-component models for a two-dimensional initial value problem reveals strengths and weaknesses of the model while demonstrating the extraction of quasi-geostrophic energy and production of small vertical scales.