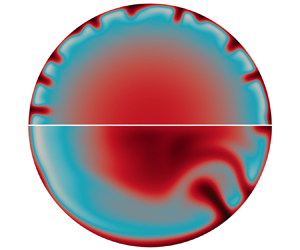
1. Introduction
Soap films are thin films of liquid stabilised by interfaces laden with surface-active agents (surfactants). In the case of free soap films, a gas phase surrounds the soap film on both sides. This is typical of liquid foams, which contain gas dispersed between (surfactant-stabilised) thin films of liquid (Fameau & Fujii Reference Fameau and Fujii2020). The stability of soap films and liquid foams is of key relevance to several applications, for example, a high foamability and foam stability is desired for shampoos (Mainkar & Jolly Reference Mainkar and Jolly2001) and fire-fighting foams (Magrabi, Dlugogorski & Jameson Reference Magrabi, Dlugogorski and Jameson2002), whilst foamability and foam stability is typically less desirable for carbonated drinks (Gonzalez Viejo et al. Reference Gonzalez Viejo, Torrico, Dunshea and Fuentes2019). Soap films thin over time due to drainage (liquid flows) and evaporation, leading to thinner films, which are less stable and more prone to rupture than thicker films (Poulain, Villermaux & Bourouiba Reference Poulain, Villermaux and Bourouiba2018). Adding magnetic nanoparticles (NPs) to soap films, to form magnetic soap films, allows for an applied magnetic field to control the drainage and stability of soap films. Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) created free magnetic soap films from aqueous-surfactant solutions containing magnetite (Fe![]() $_3$O
$_3$O![]() $_4$) NPs and reported that an inhomogeneous magnetic field can have either a stabilising or destabilising effect on a magnetic soap film, depending on the concentration of magnetite NPs in the film. It is envisaged that further research devoted to acquiring control over the dynamics and stability of magnetic soap films and further understanding the physics of these fluids could lead to the development of novel technologies. One example is the use of magnetic soap bubbles as stimuli-responsive carriers: magnetic fields could be used to control the position of magnetic soap bubbles and trigger the release of a substance, such as a drug, carried by the bubble (Soetanto & Watarai Reference Soetanto and Watarai2000; Tang et al. Reference Tang, Xiao, Sinko, Szekely and Prud'homme2015).
$_4$) NPs and reported that an inhomogeneous magnetic field can have either a stabilising or destabilising effect on a magnetic soap film, depending on the concentration of magnetite NPs in the film. It is envisaged that further research devoted to acquiring control over the dynamics and stability of magnetic soap films and further understanding the physics of these fluids could lead to the development of novel technologies. One example is the use of magnetic soap bubbles as stimuli-responsive carriers: magnetic fields could be used to control the position of magnetic soap bubbles and trigger the release of a substance, such as a drug, carried by the bubble (Soetanto & Watarai Reference Soetanto and Watarai2000; Tang et al. Reference Tang, Xiao, Sinko, Szekely and Prud'homme2015).
A wide range of physics is involved in the thinning of both soap films and magnetic soap films. In the following, a non-exhaustive introduction to the key phenomena involved in the thinning of soap films is provided. The thickness of a soap film changes with time due to drainage and evaporation. Drainage flows may be driven by gravity and by gradients in capillary pressure, where the local capillary pressure depends on the local surface tension and interface curvature (Manikantan & Squires Reference Manikantan and Squires2020). Viscous shear from drainage flows of the core liquid (the liquid in the film between the interfaces) or from a surrounding fluid can drive interfacial flows (Couder, Chomaz & Rabaud Reference Couder, Chomaz and Rabaud1989). The response of the interface depends on the type and surface coverage of surfactants adsorbed at the interface, as adsorbed surfactants resist shear and dilatational deformation. This viscous response is typically characterised through interfacial shear and dilatational viscosities (Sagis Reference Sagis2011; Li & Manikantan Reference Li and Manikantan2021). These interfacial viscosities depend on the type of surfactant and generally increase with the surface coverage of surfactant (Fruhner, Wantke & Lunkenheimer Reference Fruhner, Wantke and Lunkenheimer2000; Denkov et al. Reference Denkov, Tcholakova, Golemanov, Ananthpadmanabhan and Lips2009; Bhamla et al. Reference Bhamla, Chai, Alvarez-Valenzuela, Tajuelo and Fuller2017), which leads to less mobile interfaces. Immobile interfaces, which feature no interfacial flows, arise in the limit of large interfacial viscosities and lead to slow draining and long-lasting films (Mysels Reference Mysels1968; Bruinsma Reference Bruinsma1995). In the remainder of the text, films with surfactant-laden interfaces that are not immobile are referred to as partially mobile films, and films with interfaces clean of surface-active agents are referred to as fully mobile films. Interfacial flows advect surfactants along the interface, resulting in Marangoni stresses that can act to immobilise the interface or, alternatively, drive interfacial flows (Manikantan & Squires Reference Manikantan and Squires2020). Diffusion of surfactant along the interface and local stretching or compression of the interface also affect the interfacial surfactant concentration. It is the change in surface tension upon local stretching or compression that results in the elasticity of soap films and allows soap films to survive against disturbances (Couder et al. Reference Couder, Chomaz and Rabaud1989). When the surfactants stabilising the interface are insoluble, the change in the surface tension resulting from stretching or compression of the interface, which opposes further stretching or compression, is referred to as the Marangoni elasticity (Manikantan & Squires Reference Manikantan and Squires2020). When the surfactants are soluble, adsorption/desorption of surfactant to/from the interface additionally affects the local interfacial surfactant concentration. If an interface laden with soluble surfactants is stretched or compressed over a long enough time that adsorption/desorption affects the surface tension, the film elasticity is now referred to as the Gibbs elasticity. Many soluble surfactants also aggregate to form micelles once their concentration in the core liquid increases above the critical micelle concentration. Micelles affect adsorption/desorption kinetics (Lucassen Reference Lucassen1975) and can lead to stepwise thinning (Krichevsky & Stavans Reference Krichevsky and Stavans1997; Ochoa et al. Reference Ochoa, Gao, Srivastava and Sharma2021).
For soap films bounded by a Plateau border, a solid frame or a liquid bath, the soap film can be split into three regions (Barigou & Davidson Reference Barigou and Davidson1994): (i) a thin film region, in which the film has a thickness between several nanometres and several micrometres (Couder et al. Reference Couder, Chomaz and Rabaud1989); (ii) a meniscus with thickness of the order of a millimetre that connects the thin film to the border, frame or bath (Gennes, Brochard-Wyart & Quéré Reference Gennes, Brochard-Wyart and Quéré2004); and (iii) a transition region between the thin film and the meniscus. Liquid is sucked from the thin film into the meniscus by capillary suction, which arises since the meniscus is at a lower pressure than the thin film due to its curvature (Overbeek Reference Overbeek1960). The flow of liquid into the meniscus causes a region of reduced film thickness, known as a marginal pinch, to form in the transition region (Trégouët & Cantat Reference Trégouët and Cantat2021). Gradients in surface tension can destabilise the marginal pinch (Miguet et al. Reference Miguet, Pasquet, Rouyer, Fang and Rio2021a), resulting in marginal regeneration, an important drainage mechanism for partially mobile soap films (Mysels Reference Mysels1968; Miguet, Rouyer & Rio Reference Miguet, Rouyer and Rio2021b). According to the mechanism reported by Nierstrasz & Frens (Reference Nierstrasz and Frens1999), in marginal regeneration, elements of film with high surface coverage of surfactant are extracted from the meniscus into the thin film. These elements expand due to Marangoni stresses and become thinner as they expand, which creates extra film area that allows for the continual suction of thicker fluid into the meniscus under the constraint that the surface area of the film remains constant over time.
For soap films with thicknesses of the order of 100 nm or less, interactions between the interfaces start to become significant. Attractive (conjoining) interactions arise, for example, from van der Waals dispersion forces and act to accelerate film thinning (Bergeron Reference Bergeron1999; Stubenrauch & Von Klitzing Reference Stubenrauch and Von Klitzing2003). On the other hand, repulsive (disjoining) interactions, which act to oppose film thinning, may arise due to electrostatic interactions between electric double layers or steric interactions. The strength of these interactions is quantified by the conjoining/disjoining pressure (Bergeron & Radke Reference Bergeron and Radke1995). Assuming that the film does not rupture first, film thinning may continue until the disjoining pressure becomes large enough to prevent any further thinning. Soap films in this state are described as metastable (Couder et al. Reference Couder, Chomaz and Rabaud1989; Bergeron Reference Bergeron1999) and are either Newton black films or common black films, depending on which interactions contribute most significantly to the disjoining pressure. Common black films usually result from electric double layer forces and have equilibrium thicknesses between approximately 10 and 100 nm (Overbeek Reference Overbeek1960; Lyklema & Mysels Reference Lyklema and Mysels1965; Langevin & Sonin Reference Langevin and Sonin1994). In contrast, Newton black films are thought to be due to entropic confinement forces (Bergeron Reference Bergeron1999) and have smaller equilibrium thicknesses of around 5 nm (Overbeek Reference Overbeek1960; Couder et al. Reference Couder, Chomaz and Rabaud1989).
In addition to drainage, evaporation can have a significant effect on film thinning. The rate of evaporation is dependent on the temperature and relative humidity of the surrounding air (Miguet et al. Reference Miguet, Pasquet, Rouyer, Fang and Rio2020) and on the temperature of the film, which is affected by evaporative cooling (Boulogne, Restagno & Emmanuelle Reference Boulogne, Restagno and Emmanuelle2022). Furthermore, the presence of surfactant at the interface is expected to decrease the rate of evaporation with the precise change determined by the surface coverage of surfactant (Rubel & Gentry Reference Rubel and Gentry1984; Marek & Straub Reference Marek and Straub2001). Similarly, the presence of glycerol in the film is expected to slow the rate of evaporation (Boulogne et al. Reference Boulogne, Restagno and Emmanuelle2022; Pasquet et al. Reference Pasquet, Boulogne, Sant-Anna, Restagno and Rio2022).
When a magnetic field is applied to a soap film containing magnetic NPs, additional mechanisms need to be considered. The core liquid of a magnetic soap film is a colloidal dispersion of magnetic NPs in a non-magnetic base liquid, or a ferrofluid (Philip Reference Philip2022). Magnetite (Fe![]() $_3$O
$_3$O![]() $_4$) and maghemite (
$_4$) and maghemite (![]() $\gamma$-
$\gamma$-![]() ${\rm Fe}_2{\rm O}_3$) NPs are widely used as the magnetic NPs in ferrofluids. These NPs usually have a single magnetic domain for the particle sizes in a typical ferrofluid (Li et al. Reference Li, Kartikowati, Horie, Ogi, Iwaki and Okuyama2017; Kole & Khandekar Reference Kole and Khandekar2021). When a magnetic field is applied to a ferrofluid, the magnetic dipole moments of the magnetic NPs experience a torque driving them to align with the applied field. The ferrofluid becomes magnetised and the magnetisation will increase as the strength of the applied field is increased until saturation, which occurs when the magnetic dipole moments of all NPs is aligned with the applied field (Rosensweig Reference Rosensweig2013). If the applied magnetic field is inhomogeneous, the magnetic NPs will be driven in the direction of increasing magnetic field intensity (magnetophoresis) and a magnetically induced flow will result in the magnetic soap film due to the interaction between the NPs and the surrounding liquid molecules. The local magnetisation of a ferrofluid, which determines the strength of magnetic forcing, depends on the local concentration of magnetic NPs and varies nonlinearly with the magnetic field intensity. The local concentration of magnetic NPs is affected by magnetophoresis, flow of the base liquid, diffusion, interactions between the magnetic NPs and interactions between the magnetic NPs and other molecules in the film (Pshenichnikov, Elfimova & Ivanov Reference Pshenichnikov, Elfimova and Ivanov2011; Nacev et al. Reference Nacev, Komaee, Sarwar, Probst, Kim, Emmert-Buck and Shapiro2012; Ayansiji et al. Reference Ayansiji, Dighe, Linninger and Singh2020). Furthermore, the nonlinear relationship between the magnetisation and magnetic field intensity depends on the size distribution of magnetic NPs, magnetic dipole–dipole interactions and the thermal energy of the system, which acts to randomly orient the magnetic dipoles. In addition, the magnetisation is affected by demagnetising fields resulting from the magnetisation of the ferrofluid (Richardi & Pileni Reference Richardi and Pileni2004), which increase in importance with the concentration of magnetic NPs in the ferrofluid (Pshenichnikov & Burkova Reference Pshenichnikov and Burkova2012). An applied magnetic field can also influence the shape of the meniscus of a magnetic soap film, which may impact the strength of capillary suction (Rosensweig et al. Reference Rosensweig, Elborai, Lee and Zahn2005; Singh, Singh & Bhaumik Reference Singh, Singh and Bhaumik2024).
${\rm Fe}_2{\rm O}_3$) NPs are widely used as the magnetic NPs in ferrofluids. These NPs usually have a single magnetic domain for the particle sizes in a typical ferrofluid (Li et al. Reference Li, Kartikowati, Horie, Ogi, Iwaki and Okuyama2017; Kole & Khandekar Reference Kole and Khandekar2021). When a magnetic field is applied to a ferrofluid, the magnetic dipole moments of the magnetic NPs experience a torque driving them to align with the applied field. The ferrofluid becomes magnetised and the magnetisation will increase as the strength of the applied field is increased until saturation, which occurs when the magnetic dipole moments of all NPs is aligned with the applied field (Rosensweig Reference Rosensweig2013). If the applied magnetic field is inhomogeneous, the magnetic NPs will be driven in the direction of increasing magnetic field intensity (magnetophoresis) and a magnetically induced flow will result in the magnetic soap film due to the interaction between the NPs and the surrounding liquid molecules. The local magnetisation of a ferrofluid, which determines the strength of magnetic forcing, depends on the local concentration of magnetic NPs and varies nonlinearly with the magnetic field intensity. The local concentration of magnetic NPs is affected by magnetophoresis, flow of the base liquid, diffusion, interactions between the magnetic NPs and interactions between the magnetic NPs and other molecules in the film (Pshenichnikov, Elfimova & Ivanov Reference Pshenichnikov, Elfimova and Ivanov2011; Nacev et al. Reference Nacev, Komaee, Sarwar, Probst, Kim, Emmert-Buck and Shapiro2012; Ayansiji et al. Reference Ayansiji, Dighe, Linninger and Singh2020). Furthermore, the nonlinear relationship between the magnetisation and magnetic field intensity depends on the size distribution of magnetic NPs, magnetic dipole–dipole interactions and the thermal energy of the system, which acts to randomly orient the magnetic dipoles. In addition, the magnetisation is affected by demagnetising fields resulting from the magnetisation of the ferrofluid (Richardi & Pileni Reference Richardi and Pileni2004), which increase in importance with the concentration of magnetic NPs in the ferrofluid (Pshenichnikov & Burkova Reference Pshenichnikov and Burkova2012). An applied magnetic field can also influence the shape of the meniscus of a magnetic soap film, which may impact the strength of capillary suction (Rosensweig et al. Reference Rosensweig, Elborai, Lee and Zahn2005; Singh, Singh & Bhaumik Reference Singh, Singh and Bhaumik2024).
The speed of drainage flows is closely related to the viscosity of the draining liquid. The viscosity of a ferrofluid is larger than the viscosity of the base liquid due to the dispersed magnetic NPs (Rosensweig Reference Rosensweig2013), and the ferrofluid viscosity will increase on application of a stationary magnetic field (Odenbach & Thurm Reference Odenbach and Thurm2002), which is the magnetoviscous effect. Magnetic NPs in ferrofluids are typically coated in a surfactant to prevent them from agglomerating (Rosensweig Reference Rosensweig2013). Interactions between the surfactant coating and surfactants in the film may affect drainage flows. For example, agglomerates containing surfactant molecules and magnetite NPs formed in the magnetic soap films investigated in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023), and some of these agglomerates moved at high speeds in the direction of increasing magnetic field intensity, thus affecting drainage flows.
It is evident that the dynamics of soap films and magnetic soap films are controlled by a range of interconnected phenomena, and it is a notorious challenge to decouple and understand the effects of many of these mechanisms from experiments alone (Manikantan & Squires Reference Manikantan and Squires2020). In this context, modelling can help to reveal the relative importance of different physics and allows for predictions of film behaviour in a range of experimental conditions. In a continuum framework, thin films, bubbles and foams are frequently modelled using interface-tracking or interface-capturing methods (Tezduyar Reference Tezduyar2006), which require each interface to be followed whilst imposing mass conservation and a momentum balance at each point on the interface. These methods are computationally expensive and require sophisticated techniques to avoid spurious oscillations around each simulated interface (Denner et al. Reference Denner, Evrard, Serfaty and van Wachem2017). Thin films can also be modelled using the thin film approximation (lubrication theory), which involves capitalising on the thickness of the film being much smaller than the lateral extent of the film to derive an evolution equation for the film thickness that incorporates essential physics (O'Brien & Schwartz Reference O'Brien and Schwartz2002; Craster & Matar Reference Craster and Matar2009). Thin film models, i.e. models derived using the thin film approximation, are computationally less demanding and involve simpler numerics than interface-tracking and interface-capturing methods; therefore, we opted to derive a thin film model to describe the dynamics of soap films and magnetic soap films.
Several thin film models have been developed for the thickness of free soap films. Barigou & Davidson (Reference Barigou and Davidson1994) modelled a circular soap film bounded by copper tubes and accounted for the difference in mobility caused by varying degrees of surfactant adsorption between the thin film, the transition region and the meniscus. However, the thin film was treated simply by assuming fully mobile interfaces with a uniform velocity over the thickness. Aradian, Raphael & De Gennes (Reference Aradian, Raphael and De Gennes2001), too, considered distinct behaviour in each of the three regions, but assumed rather simplified behaviour in the thin film by treating the interfaces as immobile with a uniform surface tension. A thin film model relevant to soap films close to rupture was derived by De Wit, Gallez & Christov (Reference De Wit, Gallez and Christov1994). The resulting model consists of a system of three nonlinear equations governing the film thickness, interfacial surfactant concentration, assuming insoluble surfactants, and tangential interfacial velocity. This model has less relevance to soap films with thicknesses greater than approximately 100 nm. Schwartz & Roy (Reference Schwartz and Roy1999) assumed that the flow velocity can be divided into shear and extensional contributions and that the two flows contribute equally to the pressure gradient to derive a model for the thinning of vertical soap films. This model is expected to be valid over a greater range of thicknesses than the model of De Wit et al. (Reference De Wit, Gallez and Christov1994) and additionally includes disjoining pressure effects. Nierstrasz & Frens (Reference Nierstrasz and Frens1999) incorporated interfacial shear and dilatational viscosities, in accordance with the Boussinesq–Scriven surface stress model, into their thin film model for vertical soap films. Soluble surfactants were also considered. In order to model soluble surfactants, equations governing the surfactant concentration in the core liquid and on the interface are required in addition to relations for the rate of surfactant adsorption and desorption (Manikantan & Squires Reference Manikantan and Squires2020). For thin film models, the equation governing the concentration of surfactant in the core liquid must be integrated over the film thickness to remove the dependence on the depth coordinate, which requires the variation of surfactant concentration over the film depth to be assumed.
The aforementioned studies derive two-dimensional thin film models (film thickness as a function of one spatial dimension); therefore, marginal regeneration can not be simulated, as there can not be an exchange between thinner fluid and thicker fluid at the boundary of a thin film represented by only a single point. Joye, Hirasaki & Miller (Reference Joye, Hirasaki and Miller1996) and Naire, Braun & Snow (Reference Naire, Braun and Snow2004) derived three-dimensional thin film models for soap films (film thickness as a function of two spatial dimensions), similar to the model of Nierstrasz & Frens (Reference Nierstrasz and Frens1999) but under the assumption of insoluble surfactants. Both studies were able to simulate an instability driven by gradients in surface tension that is expected to lead to marginal regeneration. Despite these studies, marginal regeneration in a soap film has yet to be simulated using a thin film model. In addition, it is unclear why several studies have imposed a no-flux boundary condition for soap films supported by a solid wire or frame (Schwartz & Roy Reference Schwartz and Roy1999; Braun, Snow & Naire Reference Braun, Snow and Naire2002) since the thin film approximation is not valid in the meniscus and a net flow of liquid between the thin film and the meniscus is expected. Consequently, a key focus of the present study is to derive a three-dimensional thin film model and solve the resulting system with a non-zero flux boundary condition, with the aim of simulating marginal regeneration.
Several experimental studies have focused on investigating whether magnetic fields can provide an element of control over free magnetic soap films, bubbles and foams: Sudo, Hashimoto & Katagiri (Reference Sudo, Hashimoto and Katagiri1990) discovered that a magnetic field can be used to stabilise magnetic liquid foams by reducing the rate of foam coarsening. Furthermore, Hutzler et al. (Reference Hutzler, Weaire, Elias and Janiaud2002) were able to alter the structure of magnetic soap foams in cylindrical tubes using inhomogeneous magnetic fields, and Drenckhan et al. (Reference Drenckhan, Elias, Hutzler, Weaire, Janiaud and Bacri2003) were able to control the size of the bubbles forming these foams by adjusting the strength of an applied inhomogeneous magnetic field. Homogeneous magnetic fields can also affect film dynamics due to the magnetisation induced by the applied field. Elias et al. (Reference Elias, Bacri, Flament, Janiaud, Talbot, Drenckhan, Hutzler and Weaire2005) observed that the speed of drainage flows in vertical magnetic soap films was affected by the application of a homogeneous magnetic field, and Mawet et al. (Reference Mawet, Caps, Dorbolo and Elias2023) found that the shape of hemispherical magnetic soap bubbles sitting on a solid substrate was altered by an applied homogeneous magnetic field. Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) chose to adopt an inhomogeneous magnetic field in their experimental investigation of magnetic soap films, as inhomogeneous magnetic fields provide a more direct control over drainage flows through magnetophoresis. In a different configuration, inhomogeneous magnetic fields are also advantageous in that they can control the position of freely floating magnetic soap bubbles (Rodrigues et al. Reference Rodrigues, Rio, Bobroff, Langevin and Drenckhan2011). The focus of these studies investigating free magnetic soap films, bubbles and foams was predominately experimental, such that only Elias et al. (Reference Elias, Bacri, Flament, Janiaud, Talbot, Drenckhan, Hutzler and Weaire2005) developed a model for film thinning, which is a simple two-dimensional thin film model accounting for gravity, capillary and demagnetising field effects. Moulton & Pelesko (Reference Moulton and Pelesko2010) and Back & Beckham (Reference Back and Beckham2012) investigated free magnetic soap films formed on a vertical frame in inhomogeneous magnetic fields. Moulton & Pelesko (Reference Moulton and Pelesko2010) derived a two-dimensional thin film model for the film thickness, which was then extended to three dimensions by Back & Beckham (Reference Back and Beckham2012) to account for the two-dimensional nature of the applied magnetic field in the plane of the film. Although both studies found some qualitative agreement between simulated films and their experimental results, their models disregard essential physics. For example, their models make the restrictive assumption of immobile interfaces, whilst experimental images in Moulton & Pelesko (Reference Moulton and Pelesko2010) and Back & Beckham (Reference Back and Beckham2012) suggest that they were investigating partially mobile magnetic soap films (Mysels Reference Mysels1968; Bruinsma Reference Bruinsma1995). Furthermore, it was assumed that the magnetisation of the core liquid was linearly related to the applied magnetic field intensity through a constant and uniform magnetic susceptibility, which implicitly assumes that the concentration of magnetic NPs is constant and uniform and that a linear relation exists between the magnetisation and applied field intensity. Both studies adopt the no-flux boundary condition at all boundaries, which, as discussed earlier, is inconsistent with the thin film approximation only being valid within the thin film region. The modelling of magnetic soap films has received no further attention, other than the extension of the model in Moulton & Pelesko (Reference Moulton and Pelesko2010) to include disjoining pressure effects (Moulton & Lega Reference Moulton and Lega2013), such that the state of magnetic soap film modelling is rather limited.
The aim of this study is to advance the state of magnetic soap film modelling, using the experimental configuration and results in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) as a reference. The objectives of this work are then to (i) derive a model for the two-dimensional thickness field of free magnetic soap films under the action of inhomogeneous magnetic fields that includes interfacial mobility, surfactant transport, magnetite NP transport, the dependence of the film magnetisation on the magnetite NP concentration and magnetic field intensity, conjoining/disjoining pressure effects and evaporation; (ii) use the derived model to study the effect of interfacial flows on the rate of film thinning and to understand how accounting for the dependence of the magnetisation on the magnetite NP concentration affects film thickness predictions; (iii) investigate the capability of the model to predict marginal regeneration; and (iv) compare simulated films with the experimental results in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023).
The remainder of this paper is organised as follows. Section 2 provides the derivation of the model and the method for solving the system of equations governing the thickness evolution. Section 3.1 examines the contribution of interfacial flows to the rate of film thinning, and § 3.2 investigates how accounting for magnetite NP transport and the dependence of the magnetisation on the magnetite NP concentration affects film thickness predictions. Subsequently, §§ 3.3 and 3.4 present simulations that were performed to allow for a comparison with experiments, and § 4 evaluates the model by comparing these simulations with experiments. Section 4 also provides directions for future work. Concluding remarks close the paper.
2. Method
This section presents the derivation of a three-dimensional thin film model for the free soap films and magnetic soap films investigated in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023). The method for solving the resulting system of equations is then introduced and validated.
2.1. Problem description and key assumptions
The films investigated in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) were circular, almost horizontal, formed on a glass boundary, and were created from aqueous-surfactant solutions containing glycerol and dilute concentrations of magnetite NPs. A cylindrical neodymium (Nd![]() $_{2}$Fe
$_{2}$Fe![]() $_{14}$B) magnet with diameter 38.5 mm, thickness 10 mm and remanence 1.43 T was used to apply an inhomogeneous magnetic field to each film, as shown in figure 1(a). We refer the reader to Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) for additional details about the experiments.
$_{14}$B) magnet with diameter 38.5 mm, thickness 10 mm and remanence 1.43 T was used to apply an inhomogeneous magnetic field to each film, as shown in figure 1(a). We refer the reader to Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) for additional details about the experiments.

Figure 1. A schematic of a magnetic soap film supported by a glass boundary. Panel (a) illustrates the thin film region, which is the region that is modelled and simulated in the present study, in the ![]() $x$–
$x$–![]() $y$ plane. The thin film region is denoted by
$y$ plane. The thin film region is denoted by ![]() $\varOmega$; this region has boundary
$\varOmega$; this region has boundary ![]() $\partial \varOmega$ and outward-facing unit normal
$\partial \varOmega$ and outward-facing unit normal ![]() $\boldsymbol {n}_{\rm d}$. A right-handed rectangular Cartesian coordinate system with basis
$\boldsymbol {n}_{\rm d}$. A right-handed rectangular Cartesian coordinate system with basis ![]() $\{\boldsymbol {e}_{x},\boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$, coordinates
$\{\boldsymbol {e}_{x},\boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$, coordinates ![]() $\{x, y, z\}$ and origin in the bottom left of the thin film is used throughout the derivation. Panel (b) presents a zoomed-in cross-section of a small section of the thin film in (a) in the
$\{x, y, z\}$ and origin in the bottom left of the thin film is used throughout the derivation. Panel (b) presents a zoomed-in cross-section of a small section of the thin film in (a) in the ![]() $x$–
$x$–![]() $z$ plane. At the dividing surface, the outward-facing unit normal is denoted by
$z$ plane. At the dividing surface, the outward-facing unit normal is denoted by ![]() $\boldsymbol {n}$ and the tangential vector in this plane by
$\boldsymbol {n}$ and the tangential vector in this plane by ![]() $\boldsymbol {t}_x$. The thin film was assumed to be symmetrical about a centre surface, denoted by
$\boldsymbol {t}_x$. The thin film was assumed to be symmetrical about a centre surface, denoted by ![]() $z=C(x,y)$.
$z=C(x,y)$.
The phase interface that separates the core liquid from the gas phase is a three-dimensional region with a thickness of the order of a few angstroms. We modelled the phase interface by defining a two-dimensional dividing surface within the interface region (Slattery Reference Slattery1967; Sagis Reference Sagis2011). The effect of the phase interface on the surrounding phases is accounted for by defining excess quantities on the dividing surface, such as the surface tension, ![]() $\gamma$.
$\gamma$.
A rectangular Cartesian coordinate system, with basis ![]() $\{\boldsymbol {e}_{x},\boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$ and coordinates
$\{\boldsymbol {e}_{x},\boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$ and coordinates ![]() $\{x, y, z\}$, was used to derive the system of equations governing the thickness evolution of magnetic soap films. The film thickness equation was derived for the half-film thickness,
$\{x, y, z\}$, was used to derive the system of equations governing the thickness evolution of magnetic soap films. The film thickness equation was derived for the half-film thickness, ![]() $h$, by assuming symmetry about a centre surface,
$h$, by assuming symmetry about a centre surface, ![]() $C$, with uniform curvature. Since dilute concentrations of magnetite NPs in aqueous-surfactant solutions were used in the experiments to create magnetic soap films, the core liquid was modelled as a water-based ferrofluid containing a dilute concentration of magnetite NPs. Furthermore, the flow of the core liquid was modelled as an incompressible flow of a Newtonian fluid with uniform shear viscosity approximated by that of water, and magnetic dipole–dipole interactions, magnetoviscous effects and demagnetising field effects associated with the magnetisation of the film were neglected. Since the magnetic soap films in the experiments were placed in the symmetry plane of the neodymium magnet such that the applied magnetic field was approximately in the
$C$, with uniform curvature. Since dilute concentrations of magnetite NPs in aqueous-surfactant solutions were used in the experiments to create magnetic soap films, the core liquid was modelled as a water-based ferrofluid containing a dilute concentration of magnetite NPs. Furthermore, the flow of the core liquid was modelled as an incompressible flow of a Newtonian fluid with uniform shear viscosity approximated by that of water, and magnetic dipole–dipole interactions, magnetoviscous effects and demagnetising field effects associated with the magnetisation of the film were neglected. Since the magnetic soap films in the experiments were placed in the symmetry plane of the neodymium magnet such that the applied magnetic field was approximately in the ![]() $x$–
$x$–![]() $y$ plane throughout the films, the gradient
$y$ plane throughout the films, the gradient ![]() $\partial {H}/\partial {z}$ was neglected throughout the films, where
$\partial {H}/\partial {z}$ was neglected throughout the films, where ![]() $H$ is the magnitude of the magnetic field intensity. The deformation response of the interface was assumed to be governed by the Boussinesq–Scriven surface stress model with uniform surface shear and dilatational viscosities. It was also assumed, for simplicity, that the surfactants stabilising each magnetic soap film were insoluble and that the magnetite NPs in each film were monodisperse.
$H$ is the magnitude of the magnetic field intensity. The deformation response of the interface was assumed to be governed by the Boussinesq–Scriven surface stress model with uniform surface shear and dilatational viscosities. It was also assumed, for simplicity, that the surfactants stabilising each magnetic soap film were insoluble and that the magnetite NPs in each film were monodisperse.
Figure 1 presents a schematic of the modelling configuration with the coordinate system and several of the key assumptions illustrated. It should be highlighted that it is the thin film, denoted by ![]() $\varOmega$ and with boundary
$\varOmega$ and with boundary ![]() $\partial \varOmega$, that is being modelled in the present study. The following notation is used throughout: a
$\partial \varOmega$, that is being modelled in the present study. The following notation is used throughout: a ![]() $'$ is appended to fluid properties to denote that they describe the gas phase surrounding the film. When no
$'$ is appended to fluid properties to denote that they describe the gas phase surrounding the film. When no ![]() $'$ is present, the fluid properties describe the core liquid (e.g.
$'$ is present, the fluid properties describe the core liquid (e.g. ![]() $\rho '$ is the density of the surrounding gas and
$\rho '$ is the density of the surrounding gas and ![]() $\rho$ is the density of the core liquid). Furthermore, a subscript ‘
$\rho$ is the density of the core liquid). Furthermore, a subscript ‘![]() $\mathrm {s}$’ is used to denote fields defined at the dividing surface. To avoid the derivation becoming too verbose, the centre surface,
$\mathrm {s}$’ is used to denote fields defined at the dividing surface. To avoid the derivation becoming too verbose, the centre surface, ![]() $C$, is initially discarded and is reintroduced in the final equation for the thickness evolution.
$C$, is initially discarded and is reintroduced in the final equation for the thickness evolution.
2.2. Governing equations in the core liquid and at the dividing surface
The conservation of mass and balance of momentum demand
where ![]() $\rho$ is density,
$\rho$ is density, ![]() $t$ is time,
$t$ is time, ![]() $\boldsymbol {V}$ is the velocity,
$\boldsymbol {V}$ is the velocity, ![]() $\boldsymbol{\mathsf{T}}$ is the stress tensor,
$\boldsymbol{\mathsf{T}}$ is the stress tensor, ![]() $\phi$ is the conjoining pressure, through which interactions between the surfactant-laden interfaces can be accounted for (Craster & Matar Reference Craster and Matar2009), and
$\phi$ is the conjoining pressure, through which interactions between the surfactant-laden interfaces can be accounted for (Craster & Matar Reference Craster and Matar2009), and ![]() $\boldsymbol {g}$ is the gravitational acceleration, which is given by
$\boldsymbol {g}$ is the gravitational acceleration, which is given by ![]() $\boldsymbol {g} = - g \boldsymbol {e}_{z}$. The stress tensor can be expressed as
$\boldsymbol {g} = - g \boldsymbol {e}_{z}$. The stress tensor can be expressed as
where ![]() $p$ is the thermodynamic pressure,
$p$ is the thermodynamic pressure, ![]() $\boldsymbol{\mathsf{I}}$ is the identity tensor,
$\boldsymbol{\mathsf{I}}$ is the identity tensor, ![]() $\boldsymbol{\mathsf{T}}_{\mathrm {v}}$ is the viscous stress tensor and
$\boldsymbol{\mathsf{T}}_{\mathrm {v}}$ is the viscous stress tensor and ![]() $\boldsymbol{\mathsf{T}}_{\rm m}$ is the magnetic part of the stress tensor. For a Newtonian fluid,
$\boldsymbol{\mathsf{T}}_{\rm m}$ is the magnetic part of the stress tensor. For a Newtonian fluid,
where ![]() $\eta$ is the shear viscosity,
$\eta$ is the shear viscosity, ![]() $\lambda$ is the dilatational viscosity and
$\lambda$ is the dilatational viscosity and ![]() $^{\intercal }$ is the transpose operator. For a ferrofluid containing a dilute concentration of magnetite NPs and assuming magnetostriction effects are negligible (Rosensweig Reference Rosensweig2013), the magnetic part of the stress tensor given in Cowley & Rosensweig (Reference Cowley and Rosensweig1967) simplifies to
$^{\intercal }$ is the transpose operator. For a ferrofluid containing a dilute concentration of magnetite NPs and assuming magnetostriction effects are negligible (Rosensweig Reference Rosensweig2013), the magnetic part of the stress tensor given in Cowley & Rosensweig (Reference Cowley and Rosensweig1967) simplifies to
where ![]() $\mu _0$ is the permeability of free space,
$\mu _0$ is the permeability of free space, ![]() $\boldsymbol {B}$ is the magnetic flux density,
$\boldsymbol {B}$ is the magnetic flux density, ![]() $\boldsymbol {H}$ is the magnetic field intensity with magnitude
$\boldsymbol {H}$ is the magnetic field intensity with magnitude ![]() $H$ and
$H$ and ![]() $\boldsymbol {B} \boldsymbol {H}$ is the tensor product of
$\boldsymbol {B} \boldsymbol {H}$ is the tensor product of ![]() $\boldsymbol {B}$ and
$\boldsymbol {B}$ and ![]() $\boldsymbol {H}$. In the absence of demagnetising field effects due to the magnetisation of the film,
$\boldsymbol {H}$. In the absence of demagnetising field effects due to the magnetisation of the film, ![]() $\boldsymbol {H}$ is the field due to the neodymium magnet. The magnetic dipoles of the magnetite NPs rotate to align with the applied field by either Brownian relaxation (rotation of the particle) or Néel relaxation (rotation of the magnetic moment within the particle) (Rosensweig Reference Rosensweig1987). The time scale for magnetic relaxation (Rosensweig Reference Rosensweig2013) of the magnetisation,
$\boldsymbol {H}$ is the field due to the neodymium magnet. The magnetic dipoles of the magnetite NPs rotate to align with the applied field by either Brownian relaxation (rotation of the particle) or Néel relaxation (rotation of the magnetic moment within the particle) (Rosensweig Reference Rosensweig1987). The time scale for magnetic relaxation (Rosensweig Reference Rosensweig2013) of the magnetisation, ![]() $\boldsymbol {M}$, of the experimentally investigated magnetic soap films is expected to be orders of magnitude less than the characteristic flow time scale (Lalli et al. Reference Lalli, Shen, Dini and Giusti2023). As a result, the magnetisation was approximately parallel with the magnetic field intensity during the lifetime of the investigated magnetic soap films. For an electrically non-conducting fluid containing negligible displacement currents (
$\boldsymbol {M}$, of the experimentally investigated magnetic soap films is expected to be orders of magnitude less than the characteristic flow time scale (Lalli et al. Reference Lalli, Shen, Dini and Giusti2023). As a result, the magnetisation was approximately parallel with the magnetic field intensity during the lifetime of the investigated magnetic soap films. For an electrically non-conducting fluid containing negligible displacement currents (![]() $\boldsymbol {\nabla } \times \boldsymbol {H} = \boldsymbol {0}$) and with
$\boldsymbol {\nabla } \times \boldsymbol {H} = \boldsymbol {0}$) and with ![]() $\boldsymbol {M}$ and
$\boldsymbol {M}$ and ![]() $\boldsymbol {H}$ parallel, the magnetic force per unit volume,
$\boldsymbol {H}$ parallel, the magnetic force per unit volume, ![]() $\boldsymbol {f}_{\rm m} = \boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol{\mathsf{T}}_{\rm m}$, can be expressed as (Neuringer & Rosensweig Reference Neuringer and Rosensweig1964; Cowley & Rosensweig Reference Cowley and Rosensweig1967)
$\boldsymbol {f}_{\rm m} = \boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol{\mathsf{T}}_{\rm m}$, can be expressed as (Neuringer & Rosensweig Reference Neuringer and Rosensweig1964; Cowley & Rosensweig Reference Cowley and Rosensweig1967)
where ![]() $M$ is the magnitude of
$M$ is the magnitude of ![]() $\boldsymbol {M}$. When considering the flow of core liquid as an incompressible flow of a Newtonian fluid with uniform shear viscosity, the mass conservation (2.1a) and momentum balance (2.1b) with the stress tensor (2.2) inserted are
$\boldsymbol {M}$. When considering the flow of core liquid as an incompressible flow of a Newtonian fluid with uniform shear viscosity, the mass conservation (2.1a) and momentum balance (2.1b) with the stress tensor (2.2) inserted are
where ![]() $\nabla ^2$ is the Laplace operator.
$\nabla ^2$ is the Laplace operator.
The dividing surface was defined at the position of 0 surface mass density (Slattery, Sagis & Oh Reference Slattery, Sagis and Oh2007). The jump mass balance, which is a statement of conservation of mass at each point on the dividing surface, then requires (Burelbach, Bankoff & Davis Reference Burelbach, Bankoff and Davis1988; Slattery et al. Reference Slattery, Sagis and Oh2007)
where ![]() $\boldsymbol {V}_{\rm s}$ is the surface velocity (rate of change of position following a particle on the surface),
$\boldsymbol {V}_{\rm s}$ is the surface velocity (rate of change of position following a particle on the surface), ![]() $\boldsymbol {n}$ is the normal vector illustrated in figure 1 and
$\boldsymbol {n}$ is the normal vector illustrated in figure 1 and ![]() $\varSigma$ denotes the dividing surface. In continuum fluid mechanics, it is assumed that the velocity tangential to the phase interface is continuous across the phase interface (Slattery et al. Reference Slattery, Sagis and Oh2007),
$\varSigma$ denotes the dividing surface. In continuum fluid mechanics, it is assumed that the velocity tangential to the phase interface is continuous across the phase interface (Slattery et al. Reference Slattery, Sagis and Oh2007),
where ![]() $\boldsymbol{\mathsf{P}}_{\rm s}$ is the surface projection tensor, defined by
$\boldsymbol{\mathsf{P}}_{\rm s}$ is the surface projection tensor, defined by ![]() $\boldsymbol{\mathsf{P}}_{\rm s} = \boldsymbol{\mathsf{I}} - \boldsymbol {n} \boldsymbol {n}$. The mass flux due to evaporation,
$\boldsymbol{\mathsf{P}}_{\rm s} = \boldsymbol{\mathsf{I}} - \boldsymbol {n} \boldsymbol {n}$. The mass flux due to evaporation, ![]() $J_{\rm e}$, is given by (Burelbach et al. Reference Burelbach, Bankoff and Davis1988; Bai & Gosman Reference Bai and Gosman1996)
$J_{\rm e}$, is given by (Burelbach et al. Reference Burelbach, Bankoff and Davis1988; Bai & Gosman Reference Bai and Gosman1996)
Therefore, ![]() $\boldsymbol {V}$ is only equal to
$\boldsymbol {V}$ is only equal to ![]() $\boldsymbol {V}_{\rm s}$ at the dividing surface when there is no evaporation. The jump momentum balance, which is a statement of momentum balance at each point on the dividing surface, requires (Slattery et al. Reference Slattery, Sagis and Oh2007)
$\boldsymbol {V}_{\rm s}$ at the dividing surface when there is no evaporation. The jump momentum balance, which is a statement of momentum balance at each point on the dividing surface, requires (Slattery et al. Reference Slattery, Sagis and Oh2007)
where ![]() $\boldsymbol {\nabla }_{\rm s}$ and
$\boldsymbol {\nabla }_{\rm s}$ and ![]() $\boldsymbol {\nabla }_{\rm s} \boldsymbol {\cdot }$ are the surface gradient and surface divergence operators, respectively, and
$\boldsymbol {\nabla }_{\rm s} \boldsymbol {\cdot }$ are the surface gradient and surface divergence operators, respectively, and ![]() $\boldsymbol{\mathsf{T}}_{\rm s}$ is the surface stress tensor. Appendix A provides additional details about these surface operators. The surface stress tensor
$\boldsymbol{\mathsf{T}}_{\rm s}$ is the surface stress tensor. Appendix A provides additional details about these surface operators. The surface stress tensor ![]() $\boldsymbol{\mathsf{T}}_{\rm s}$ can be expressed as the sum of contributions due to the surface tension,
$\boldsymbol{\mathsf{T}}_{\rm s}$ can be expressed as the sum of contributions due to the surface tension, ![]() $\gamma$, and a surface stress tensor
$\gamma$, and a surface stress tensor ![]() $\boldsymbol{\mathsf{S}}_{\rm s}$ that accounts for surface viscous effects due to the presence of surfactant molecules at the phase interface,
$\boldsymbol{\mathsf{S}}_{\rm s}$ that accounts for surface viscous effects due to the presence of surfactant molecules at the phase interface,
Using the surface stress tensor (2.11) and the stress tensor (2.2) in the jump momentum balance (2.10) results in
 \begin{align} &\boldsymbol{\nabla}_{\rm s} \gamma + 2 \kappa \gamma \boldsymbol{n} + \boldsymbol{\nabla}_{\rm s} \boldsymbol{\cdot} \boldsymbol{\mathsf{S}}_{\rm s} + (p - p')\boldsymbol{n} + (\boldsymbol{\mathsf{T}}_{\mathrm{v}}' - \boldsymbol{\mathsf{T}}_{\mathrm{v}}) \boldsymbol{\cdot} \boldsymbol{n} + (\boldsymbol{\mathsf{T}}_{\rm m}' - \boldsymbol{\mathsf{T}}_{\rm m}) \boldsymbol{\cdot} \boldsymbol{n}\nonumber\\ &\quad = \frac{J_{\rm e}^2}{\rho'}\left(1 - \frac{\rho'}{\rho} \right) \boldsymbol{n} \quad \text{at } \varSigma , \end{align}
\begin{align} &\boldsymbol{\nabla}_{\rm s} \gamma + 2 \kappa \gamma \boldsymbol{n} + \boldsymbol{\nabla}_{\rm s} \boldsymbol{\cdot} \boldsymbol{\mathsf{S}}_{\rm s} + (p - p')\boldsymbol{n} + (\boldsymbol{\mathsf{T}}_{\mathrm{v}}' - \boldsymbol{\mathsf{T}}_{\mathrm{v}}) \boldsymbol{\cdot} \boldsymbol{n} + (\boldsymbol{\mathsf{T}}_{\rm m}' - \boldsymbol{\mathsf{T}}_{\rm m}) \boldsymbol{\cdot} \boldsymbol{n}\nonumber\\ &\quad = \frac{J_{\rm e}^2}{\rho'}\left(1 - \frac{\rho'}{\rho} \right) \boldsymbol{n} \quad \text{at } \varSigma , \end{align}
where ![]() $\kappa$ is the mean curvature at each point on the dividing surface, which is given by
$\kappa$ is the mean curvature at each point on the dividing surface, which is given by
For a non-magnetisable gas surrounding the magnetic soap film and from the magnetostatic equations (Rosensweig Reference Rosensweig2013),
The Boussinesq–Scriven surface stress model is a surface analogue of the stress deformation relation for a Newtonian fluid. With the Boussinesq–Scriven surface stress model (Slattery et al. Reference Slattery, Sagis and Oh2007),
where ![]() $\eta _{\rm s}$ and
$\eta _{\rm s}$ and ![]() $\lambda _{\rm s}$ are the surface shear and surface dilatational viscosities, respectively, and
$\lambda _{\rm s}$ are the surface shear and surface dilatational viscosities, respectively, and ![]() $\boldsymbol{\mathsf{D}}_{\rm s}$ is the surface rate of deformation tensor, which is given by
$\boldsymbol{\mathsf{D}}_{\rm s}$ is the surface rate of deformation tensor, which is given by
Taking the inner product of (2.12) with three linearly independent vectors leads to three scalar jump momentum balance equations, which serve as boundary conditions for the governing equations in the core liquid (2.6). It is convenient to use ![]() $\{\boldsymbol {t}_x, \boldsymbol {t}_y, \boldsymbol {n}\}$, where
$\{\boldsymbol {t}_x, \boldsymbol {t}_y, \boldsymbol {n}\}$, where ![]() $\boldsymbol {t}_x$ and
$\boldsymbol {t}_x$ and ![]() $\boldsymbol {t}_y$ are two linearly independent vectors tangential to the film surface. In terms of the half-film thickness,
$\boldsymbol {t}_y$ are two linearly independent vectors tangential to the film surface. In terms of the half-film thickness, ![]() $\{\boldsymbol {t}_x, \boldsymbol {t}_y, \boldsymbol {n}\}$ are
$\{\boldsymbol {t}_x, \boldsymbol {t}_y, \boldsymbol {n}\}$ are
 $$\begin{gather} \boldsymbol{t}_{x} = \left(1 + \left(\frac{\partial h}{\partial x}\right)^2 \right)^{-{1}/{2}} \left( \boldsymbol{e}_{x} + \frac{\partial{h}}{\partial{x}} \boldsymbol{e}_{z} \right) , \end{gather}$$
$$\begin{gather} \boldsymbol{t}_{x} = \left(1 + \left(\frac{\partial h}{\partial x}\right)^2 \right)^{-{1}/{2}} \left( \boldsymbol{e}_{x} + \frac{\partial{h}}{\partial{x}} \boldsymbol{e}_{z} \right) , \end{gather}$$ $$\begin{gather}\boldsymbol{t}_{y} = \left(1 + \left(\frac{\partial h}{\partial y}\right)^2 \right)^{-{1}/{2}} \left( \boldsymbol{e}_{y} + \frac{\partial{h}}{\partial{y}} \boldsymbol{e}_{z} \right) , \end{gather}$$
$$\begin{gather}\boldsymbol{t}_{y} = \left(1 + \left(\frac{\partial h}{\partial y}\right)^2 \right)^{-{1}/{2}} \left( \boldsymbol{e}_{y} + \frac{\partial{h}}{\partial{y}} \boldsymbol{e}_{z} \right) , \end{gather}$$ $$\begin{gather}\boldsymbol{n} = \left(1 + \left(\frac{\partial h}{\partial x}\right)^{2} + \left(\frac{\partial h}{\partial y}\right)^{2} \right)^{-{1}/{2}} \left( -\frac{\partial{h}}{\partial{x}} \boldsymbol{e}_{x} - \frac{\partial{h}}{\partial{y}} \boldsymbol{e}_{y} + \boldsymbol{e}_{z} \right) . \end{gather}$$
$$\begin{gather}\boldsymbol{n} = \left(1 + \left(\frac{\partial h}{\partial x}\right)^{2} + \left(\frac{\partial h}{\partial y}\right)^{2} \right)^{-{1}/{2}} \left( -\frac{\partial{h}}{\partial{x}} \boldsymbol{e}_{x} - \frac{\partial{h}}{\partial{y}} \boldsymbol{e}_{y} + \boldsymbol{e}_{z} \right) . \end{gather}$$ Another condition that must be satisfied at the dividing surface is the kinematic boundary condition, which states that for a function ![]() $\varPhi$ that is 0 at each point on the dividing surface (Slattery et al. Reference Slattery, Sagis and Oh2007)
$\varPhi$ that is 0 at each point on the dividing surface (Slattery et al. Reference Slattery, Sagis and Oh2007)
In this instance, ![]() $\varPhi (x,y,z,t) = z - h(x,y,t)$, and the kinematic boundary condition (2.18) is
$\varPhi (x,y,z,t) = z - h(x,y,t)$, and the kinematic boundary condition (2.18) is
where ![]() $\{u_{\rm s}, v_{\rm s}, w_{\rm s}\}$ are the rectangular Cartesian components of
$\{u_{\rm s}, v_{\rm s}, w_{\rm s}\}$ are the rectangular Cartesian components of ![]() $\boldsymbol {V}_{\rm s}$. Furthermore, symmetry boundary conditions are used at the mid-plane of the film,
$\boldsymbol {V}_{\rm s}$. Furthermore, symmetry boundary conditions are used at the mid-plane of the film,
where ![]() $\{u, v, w\}$ are the rectangular Cartesian components of
$\{u, v, w\}$ are the rectangular Cartesian components of ![]() $\boldsymbol {V}$.
$\boldsymbol {V}$.
2.3. Thin film approximation
With a characteristic thickness scale ![]() $\mathcal {H}$ and a characteristic length scale
$\mathcal {H}$ and a characteristic length scale ![]() $L$, the dimensionless coordinates and thickness are
$L$, the dimensionless coordinates and thickness are
where ![]() $\tilde {\phantom {-}}$ denotes a dimensionless variable. The thin film approximation (or lubrication approximation) involves capitalising on the small size of the thin film parameter,
$\tilde {\phantom {-}}$ denotes a dimensionless variable. The thin film approximation (or lubrication approximation) involves capitalising on the small size of the thin film parameter, ![]() $\epsilon$, which is defined by
$\epsilon$, which is defined by
All equations are written in dimensionless form and the dominant physics is extracted by expanding dimensionless dependent variables using a series expansion in powers of ![]() $\epsilon$, for example,
$\epsilon$, for example,
and retaining terms at leading order in ![]() $\epsilon$. The velocity scale
$\epsilon$. The velocity scale ![]() $U$, pressure scale
$U$, pressure scale ![]() $P$ and scales
$P$ and scales ![]() $M_{{\rm c}}$ and
$M_{{\rm c}}$ and ![]() $H_{{\rm c}}$ for the magnetisation and magnetic field intensity are used to introduce the following dimensionless variables:
$H_{{\rm c}}$ for the magnetisation and magnetic field intensity are used to introduce the following dimensionless variables:
 \begin{equation} \left.\begin{gathered} \tilde{u} = \frac{u}{U} , \quad \tilde{v} = \frac{v}{U} , \quad \tilde{w} = \frac{w}{\epsilon U} , \quad \tilde{u}_{\rm s} = \frac{u_{\rm s}}{U} , \quad \tilde{v}_{\mathrm{s}} = \frac{v_{\rm s}}{U} , \quad \tilde{w}_{\rm s} = \frac{w_{\rm s}}{\epsilon U},\\ \tilde{t} = \frac{t U}{L} ,\quad \tilde{p} = \frac{p}{P} , \quad \tilde{\phi} = \frac{\phi}{P} ,\quad \tilde{M}_x= \frac{M_x}{M_{\mathrm{c}}} , \quad \tilde{M}_y = \frac{M_y}{M_{\mathrm{c}}} ,\\ \tilde{M}_z = \frac{M_z}{\epsilon M_{\mathrm{c}}} , \quad \tilde{M} = \frac{M}{M_\mathrm{c}} , \quad \tilde{H} = \frac{H}{H_\mathrm{c}} . \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \tilde{u} = \frac{u}{U} , \quad \tilde{v} = \frac{v}{U} , \quad \tilde{w} = \frac{w}{\epsilon U} , \quad \tilde{u}_{\rm s} = \frac{u_{\rm s}}{U} , \quad \tilde{v}_{\mathrm{s}} = \frac{v_{\rm s}}{U} , \quad \tilde{w}_{\rm s} = \frac{w_{\rm s}}{\epsilon U},\\ \tilde{t} = \frac{t U}{L} ,\quad \tilde{p} = \frac{p}{P} , \quad \tilde{\phi} = \frac{\phi}{P} ,\quad \tilde{M}_x= \frac{M_x}{M_{\mathrm{c}}} , \quad \tilde{M}_y = \frac{M_y}{M_{\mathrm{c}}} ,\\ \tilde{M}_z = \frac{M_z}{\epsilon M_{\mathrm{c}}} , \quad \tilde{M} = \frac{M}{M_\mathrm{c}} , \quad \tilde{H} = \frac{H}{H_\mathrm{c}} . \end{gathered}\right\} \end{equation}
Here ![]() $\{M_x, M_y, M_z\}$ are the rectangular Cartesian components of the magnetisation
$\{M_x, M_y, M_z\}$ are the rectangular Cartesian components of the magnetisation ![]() $\boldsymbol {M}$. Note that
$\boldsymbol {M}$. Note that ![]() $M_z$ has been scaled by
$M_z$ has been scaled by ![]() $\epsilon M_{\mathrm{c}}$ as it is expected that
$\epsilon M_{\mathrm{c}}$ as it is expected that ![]() $M_z \ll M_x$ and
$M_z \ll M_x$ and ![]() $M_z \ll M_y$ due to the direction of the applied magnetic field. From (2.8), we find at leading order in
$M_z \ll M_y$ due to the direction of the applied magnetic field. From (2.8), we find at leading order in ![]() $\epsilon$ that
$\epsilon$ that
We use (2.25) with the kinematic boundary condition (2.19) and the result of integrating the continuity equation (2.6a) over the film thickness using the Leibniz integral rule and the symmetry boundary condition (2.20) to find that
where ![]() $Q_x$ and
$Q_x$ and ![]() $Q_y$ are the following depth-integrated velocities:
$Q_y$ are the following depth-integrated velocities:
At leading order in ![]() $\epsilon$ and at the dividing surface,
$\epsilon$ and at the dividing surface, ![]() $(\boldsymbol {V} - \boldsymbol {V}_{\rm s}) \boldsymbol {\cdot } \boldsymbol {n} = w(x,y,z=h,t) - w_{\rm s}$, which allows the mass flux due to evaporation to be introduced into (2.26),
$(\boldsymbol {V} - \boldsymbol {V}_{\rm s}) \boldsymbol {\cdot } \boldsymbol {n} = w(x,y,z=h,t) - w_{\rm s}$, which allows the mass flux due to evaporation to be introduced into (2.26),
In dimensionless form, (2.28) reads
where
 \begin{equation} \tilde{Q}_x = \int_{0}^{\tilde{h}} \tilde{u} \, \mathrm{d} \tilde{z} = \frac{Q_x}{U\mathcal{H}} , \quad \tilde{Q}_y = \int_{0}^{\tilde{h}} \tilde{v} \, \mathrm{d} \tilde{z} = \frac{Q_y}{U\mathcal{H}} , \quad \tilde{J}_{\rm e} = \frac{J_{\rm e}}{\rho U \epsilon} . \end{equation}
\begin{equation} \tilde{Q}_x = \int_{0}^{\tilde{h}} \tilde{u} \, \mathrm{d} \tilde{z} = \frac{Q_x}{U\mathcal{H}} , \quad \tilde{Q}_y = \int_{0}^{\tilde{h}} \tilde{v} \, \mathrm{d} \tilde{z} = \frac{Q_y}{U\mathcal{H}} , \quad \tilde{J}_{\rm e} = \frac{J_{\rm e}}{\rho U \epsilon} . \end{equation}
The focus now turns to finding ![]() $\tilde {u}$ and
$\tilde {u}$ and ![]() $\tilde {v}$ so that
$\tilde {v}$ so that ![]() $\tilde {Q}_x$ and
$\tilde {Q}_x$ and ![]() $\tilde {Q}_y$ can be evaluated. The pressure scale
$\tilde {Q}_y$ can be evaluated. The pressure scale ![]() $P = {\eta U}/{L}$ is relevant to extensional (plug) flows (Kargupta, Sharma & Khanna Reference Kargupta, Sharma and Khanna2004; Münch, Wagner & Witelski Reference Münch, Wagner and Witelski2005). Since we expect viscous shear from the core liquid to enter the problem at leading order, we instead use the pressure scale
$P = {\eta U}/{L}$ is relevant to extensional (plug) flows (Kargupta, Sharma & Khanna Reference Kargupta, Sharma and Khanna2004; Münch, Wagner & Witelski Reference Münch, Wagner and Witelski2005). Since we expect viscous shear from the core liquid to enter the problem at leading order, we instead use the pressure scale ![]() $P = {\eta U}/(\epsilon \mathcal {H})$, which allows the derived model to be used in the limit of immobile interfaces. With the pressure scale
$P = {\eta U}/(\epsilon \mathcal {H})$, which allows the derived model to be used in the limit of immobile interfaces. With the pressure scale ![]() $P = {\eta U}/(\epsilon \mathcal {H})$, the governing equations for the core liquid (2.6) in dimensionless form are
$P = {\eta U}/(\epsilon \mathcal {H})$, the governing equations for the core liquid (2.6) in dimensionless form are
 \begin{gather} \epsilon Re \left( \frac{\partial \tilde{u}}{\partial \tilde{t}} + \tilde{u}\frac{\partial \tilde{u}}{\partial \tilde{x}} + \tilde{v}\frac{\partial \tilde{u}}{\partial \tilde{y}} + \tilde{w}\frac{\partial \tilde{u}}{\partial \tilde{z}}\right) =-& \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{x}} + \epsilon^2 \left(\frac{\partial^{2} \tilde{u}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{u}}{\partial \tilde{y}^{2}}\right)\nonumber\\ &+ \,\frac{\partial^{2} \tilde{u}}{\partial \tilde{z}^{2}} + \varPsi \tilde{M}\frac{\partial \tilde{H}}{\partial \tilde{x}} , \end{gather}
\begin{gather} \epsilon Re \left( \frac{\partial \tilde{u}}{\partial \tilde{t}} + \tilde{u}\frac{\partial \tilde{u}}{\partial \tilde{x}} + \tilde{v}\frac{\partial \tilde{u}}{\partial \tilde{y}} + \tilde{w}\frac{\partial \tilde{u}}{\partial \tilde{z}}\right) =-& \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{x}} + \epsilon^2 \left(\frac{\partial^{2} \tilde{u}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{u}}{\partial \tilde{y}^{2}}\right)\nonumber\\ &+ \,\frac{\partial^{2} \tilde{u}}{\partial \tilde{z}^{2}} + \varPsi \tilde{M}\frac{\partial \tilde{H}}{\partial \tilde{x}} , \end{gather} \begin{gather} \epsilon Re \left( \frac{\partial \tilde{v}}{\partial \tilde{t}} + \tilde{u}\frac{\partial \tilde{v}}{\partial \tilde{x}} + \tilde{v}\frac{\partial \tilde{v}}{\partial \tilde{y}} + \tilde{w}\frac{\partial \tilde{v}}{\partial \tilde{z}} \right) =-& \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{y}} + \epsilon^2 \left( \frac{\partial^{2} \tilde{v}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{v}}{\partial \tilde{y}^{2}} \right)\nonumber\\ &+\, \frac{\partial^{2} \tilde{v}}{\partial \tilde{z}^{2}} + \varPsi \tilde{M}\frac{\partial \tilde{H}}{\partial \tilde{y}}, \end{gather}
\begin{gather} \epsilon Re \left( \frac{\partial \tilde{v}}{\partial \tilde{t}} + \tilde{u}\frac{\partial \tilde{v}}{\partial \tilde{x}} + \tilde{v}\frac{\partial \tilde{v}}{\partial \tilde{y}} + \tilde{w}\frac{\partial \tilde{v}}{\partial \tilde{z}} \right) =-& \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{y}} + \epsilon^2 \left( \frac{\partial^{2} \tilde{v}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{v}}{\partial \tilde{y}^{2}} \right)\nonumber\\ &+\, \frac{\partial^{2} \tilde{v}}{\partial \tilde{z}^{2}} + \varPsi \tilde{M}\frac{\partial \tilde{H}}{\partial \tilde{y}}, \end{gather} \begin{gather} \epsilon^3 Re \left( \frac{\partial \tilde{w}}{\partial \tilde{t}} + \tilde{u} \frac{\partial \tilde{w}}{\partial \tilde{x}} + \tilde{v} \frac{\partial \tilde{w}}{\partial \tilde{y}} + \tilde{w} \frac{\partial \tilde{w}}{\partial \tilde{z}} \right) =&-\frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{z}} + \epsilon^4 \left( \frac{\partial^{2} \tilde{w}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{w}}{\partial \tilde{y}^{2}} \right)\nonumber\\ &+ \,\epsilon^2 \frac{\partial^{2} \tilde{w}}{\partial \tilde{z}^{2}} - \epsilon \mathcal{G} , \end{gather}
\begin{gather} \epsilon^3 Re \left( \frac{\partial \tilde{w}}{\partial \tilde{t}} + \tilde{u} \frac{\partial \tilde{w}}{\partial \tilde{x}} + \tilde{v} \frac{\partial \tilde{w}}{\partial \tilde{y}} + \tilde{w} \frac{\partial \tilde{w}}{\partial \tilde{z}} \right) =&-\frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{z}} + \epsilon^4 \left( \frac{\partial^{2} \tilde{w}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{w}}{\partial \tilde{y}^{2}} \right)\nonumber\\ &+ \,\epsilon^2 \frac{\partial^{2} \tilde{w}}{\partial \tilde{z}^{2}} - \epsilon \mathcal{G} , \end{gather}
where ![]() $Re$ is the Reynolds number,
$Re$ is the Reynolds number, ![]() $\varPsi$ is a dimensionless magnetic number and
$\varPsi$ is a dimensionless magnetic number and ![]() $\mathcal {G}$ is a dimensionless gravitational number. These dimensionless numbers are defined by
$\mathcal {G}$ is a dimensionless gravitational number. These dimensionless numbers are defined by
The Reynolds number can be expressed as ![]() $Re = \epsilon Re^{\star }$, where
$Re = \epsilon Re^{\star }$, where ![]() $Re^{\star }$ is of the order of 1 or less. As a result, (2.31) at leading order in
$Re^{\star }$ is of the order of 1 or less. As a result, (2.31) at leading order in ![]() $\epsilon$ is
$\epsilon$ is
The subscript 0s in (2.33), which come from the series expansion detailed in (2.23), indicate that leading-order terms have been retained. For brevity, the subscript 0s are omitted in the remainder of the text.
The surface tension was scaled using the maximum surface pressure, ![]() $S$,
$S$,
where ![]() $\gamma _{\textrm{sat}}$ is the surface tension of an interface saturated with surfactant and
$\gamma _{\textrm{sat}}$ is the surface tension of an interface saturated with surfactant and ![]() $\gamma _{{\rm c}}$ is the surface tension of a clean interface, i.e. an interface free of surface-active agents. Assuming viscous stresses in the gas phase can be neglected and introducing
$\gamma _{{\rm c}}$ is the surface tension of a clean interface, i.e. an interface free of surface-active agents. Assuming viscous stresses in the gas phase can be neglected and introducing ![]() $\rho ' = \epsilon \rho$, the inner product of the jump momentum balance (2.12) with
$\rho ' = \epsilon \rho$, the inner product of the jump momentum balance (2.12) with ![]() $\boldsymbol {n}$ when retaining each term at its leading order in
$\boldsymbol {n}$ when retaining each term at its leading order in ![]() $\epsilon$ is
$\epsilon$ is
 \begin{align} \tilde{p} &= \tilde{p}' -
\left(\frac{\partial^{2} \tilde{h}}{\partial \tilde{x}^{2}}
+ \frac{\partial^{2} \tilde{h}}{\partial \tilde{y}^{2}}
\right)\left(\epsilon^2 \mathcal{M} \tilde{ \gamma} +
\frac{\epsilon^3}{\mathcal{C}}\right) + \tilde{J}_{\rm e}^2
\epsilon^3 Re^{{\star}} (1-\epsilon) \nonumber\\
&\quad- \epsilon^2 \textit{Bq}_{\mathrm{sh}} \left( \frac{\partial
\tilde{u}_{{\rm s}}}{\partial \tilde{x}} \left(\frac{\partial^{2}
\tilde{h}}{\partial \tilde{x}^{2}} - \frac{\partial^{2}
\tilde{h}}{\partial \tilde{y}^{2}}\right) + 2
\frac{\partial^{2} \tilde{h}}{\partial \tilde{x} \partial
\tilde{y}} \left( \frac{\partial \tilde{u}_{{\rm s}}}{\partial
\tilde{y}} + \frac{\partial \tilde{v}_{{\rm s}}}{\partial
\tilde{x}} \right) + \frac{\partial \tilde{v}_{{\rm s}}}{\partial
\tilde{y}} \left( \frac{\partial^{2} \tilde{h}}{\partial
\tilde{y}^{2}} - \frac{\partial^{2} \tilde{h}}{\partial
\tilde{x}^{2}} \right) \right)\nonumber\\ &\quad-
\epsilon^2 \textit{Bq}_{\rm d} \left( \frac{\partial^{2}
\tilde{h}}{\partial \tilde{x}^{2}} + \frac{\partial^{2}
\tilde{h}}{\partial \tilde{y}^{2}} \right) \left(
\frac{\partial \tilde{u}_{\rm s}}{\partial \tilde{x}} +
\frac{\partial \tilde{v}_{\rm s}}{\partial \tilde{y}}
\right) + 2 \epsilon^2 \left(-\frac{\partial
\tilde{u}}{\partial \tilde{z}} \frac{\partial
\tilde{h}}{\partial \tilde{x}} - \frac{\partial
\tilde{v}}{\partial \tilde{z}} \frac{\partial
\tilde{h}}{\partial \tilde{y}} + \frac{\partial
\tilde{w}}{\partial \tilde{z}} \right)\nonumber\\ &\quad -
\frac{1}{2} \frac{M_\mathrm{c}}{H_\mathrm{c}} \epsilon^2
\varPsi \left( - \tilde{M}_x \frac{\partial
\tilde{h}}{\partial \tilde{x}} - \tilde{M}_y \frac{\partial
\tilde{h}}{\partial \tilde{y}} + \tilde{M}_z \right)^2
\quad \text{at } \varSigma ,
\end{align}
\begin{align} \tilde{p} &= \tilde{p}' -
\left(\frac{\partial^{2} \tilde{h}}{\partial \tilde{x}^{2}}
+ \frac{\partial^{2} \tilde{h}}{\partial \tilde{y}^{2}}
\right)\left(\epsilon^2 \mathcal{M} \tilde{ \gamma} +
\frac{\epsilon^3}{\mathcal{C}}\right) + \tilde{J}_{\rm e}^2
\epsilon^3 Re^{{\star}} (1-\epsilon) \nonumber\\
&\quad- \epsilon^2 \textit{Bq}_{\mathrm{sh}} \left( \frac{\partial
\tilde{u}_{{\rm s}}}{\partial \tilde{x}} \left(\frac{\partial^{2}
\tilde{h}}{\partial \tilde{x}^{2}} - \frac{\partial^{2}
\tilde{h}}{\partial \tilde{y}^{2}}\right) + 2
\frac{\partial^{2} \tilde{h}}{\partial \tilde{x} \partial
\tilde{y}} \left( \frac{\partial \tilde{u}_{{\rm s}}}{\partial
\tilde{y}} + \frac{\partial \tilde{v}_{{\rm s}}}{\partial
\tilde{x}} \right) + \frac{\partial \tilde{v}_{{\rm s}}}{\partial
\tilde{y}} \left( \frac{\partial^{2} \tilde{h}}{\partial
\tilde{y}^{2}} - \frac{\partial^{2} \tilde{h}}{\partial
\tilde{x}^{2}} \right) \right)\nonumber\\ &\quad-
\epsilon^2 \textit{Bq}_{\rm d} \left( \frac{\partial^{2}
\tilde{h}}{\partial \tilde{x}^{2}} + \frac{\partial^{2}
\tilde{h}}{\partial \tilde{y}^{2}} \right) \left(
\frac{\partial \tilde{u}_{\rm s}}{\partial \tilde{x}} +
\frac{\partial \tilde{v}_{\rm s}}{\partial \tilde{y}}
\right) + 2 \epsilon^2 \left(-\frac{\partial
\tilde{u}}{\partial \tilde{z}} \frac{\partial
\tilde{h}}{\partial \tilde{x}} - \frac{\partial
\tilde{v}}{\partial \tilde{z}} \frac{\partial
\tilde{h}}{\partial \tilde{y}} + \frac{\partial
\tilde{w}}{\partial \tilde{z}} \right)\nonumber\\ &\quad -
\frac{1}{2} \frac{M_\mathrm{c}}{H_\mathrm{c}} \epsilon^2
\varPsi \left( - \tilde{M}_x \frac{\partial
\tilde{h}}{\partial \tilde{x}} - \tilde{M}_y \frac{\partial
\tilde{h}}{\partial \tilde{y}} + \tilde{M}_z \right)^2
\quad \text{at } \varSigma ,
\end{align}
where ![]() $\mathcal {M}$ is the Marangoni number,
$\mathcal {M}$ is the Marangoni number, ![]() $\mathcal {C}$ is the capillary number, and
$\mathcal {C}$ is the capillary number, and ![]() $\textit {Bq}_{\mathrm {sh}}$ and
$\textit {Bq}_{\mathrm {sh}}$ and ![]() $\textit {Bq}_{\rm d}$ are the shear and dilatational Boussinesq numbers, respectively. These dimensionless numbers are defined by
$\textit {Bq}_{\rm d}$ are the shear and dilatational Boussinesq numbers, respectively. These dimensionless numbers are defined by
We used the surrounding gas pressure as the reference pressure, i.e. ![]() $\tilde {p}' = 0$. Integrating the leading-order
$\tilde {p}' = 0$. Integrating the leading-order ![]() $z$-momentum equation (2.33d) in
$z$-momentum equation (2.33d) in ![]() $z$ and using (2.35) as a boundary condition leads to
$z$ and using (2.35) as a boundary condition leads to
 \begin{equation} \tilde{p} + \tilde{\phi} = \epsilon \mathcal{G} (\tilde{h} - \tilde{z}) - \left(\frac{\partial^{2} \tilde{h}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{h}}{\partial \tilde{y}^{2}}\right) \left(\epsilon^2 \mathcal{M} \tilde{\gamma} + \frac{\epsilon^3}{\mathcal{C}}\right) - \tilde{ \varPi} , \end{equation}
\begin{equation} \tilde{p} + \tilde{\phi} = \epsilon \mathcal{G} (\tilde{h} - \tilde{z}) - \left(\frac{\partial^{2} \tilde{h}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{h}}{\partial \tilde{y}^{2}}\right) \left(\epsilon^2 \mathcal{M} \tilde{\gamma} + \frac{\epsilon^3}{\mathcal{C}}\right) - \tilde{ \varPi} , \end{equation}
where ![]() $\tilde { \varPi }$ is the dimensionless disjoining pressure, which is related to the conjoining pressure by
$\tilde { \varPi }$ is the dimensionless disjoining pressure, which is related to the conjoining pressure by ![]() $\tilde { \varPi } = - \tilde { \phi }$, and several lower-order terms from (2.35) have been discarded. Having obtained an expression for the pressure, the leading-order
$\tilde { \varPi } = - \tilde { \phi }$, and several lower-order terms from (2.35) have been discarded. Having obtained an expression for the pressure, the leading-order ![]() $x$-momentum (2.33b) and
$x$-momentum (2.33b) and ![]() $y$-momentum (2.33c) equations can be integrated twice in
$y$-momentum (2.33c) equations can be integrated twice in ![]() $z$ with the symmetry boundary condition (2.20) and the continuity of tangential velocity across the interface (2.25) to obtain
$z$ with the symmetry boundary condition (2.20) and the continuity of tangential velocity across the interface (2.25) to obtain
 $$\begin{gather} \tilde{u} = \tilde{u}_{\rm s} + \frac{1}{2}(\tilde{z}^2 - \tilde{h}^2)\left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{x}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{x}} \right) , \end{gather}$$
$$\begin{gather} \tilde{u} = \tilde{u}_{\rm s} + \frac{1}{2}(\tilde{z}^2 - \tilde{h}^2)\left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{x}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{x}} \right) , \end{gather}$$ $$\begin{gather}\tilde{v} = \tilde{v}_{\rm s} + \frac{1}{2}(\tilde{z}^2 - \tilde{h}^2)\left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{y}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{y}} \right) . \end{gather}$$
$$\begin{gather}\tilde{v} = \tilde{v}_{\rm s} + \frac{1}{2}(\tilde{z}^2 - \tilde{h}^2)\left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{y}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{y}} \right) . \end{gather}$$
In deriving (2.38), it was assumed that the magnetisation does not vary over the film depth, as is discussed further in § 2.4. At this point, equations are needed to define the surface velocity components present in (2.38). By taking the inner product of the jump momentum balance (2.12) with ![]() $\boldsymbol {t}_x$ and
$\boldsymbol {t}_x$ and ![]() $\boldsymbol {t}_y$, two equations governing
$\boldsymbol {t}_y$, two equations governing ![]() $u_{\rm s}$ and
$u_{\rm s}$ and ![]() $v_{\rm s}$ can be derived. Taking each term in the inner products at leading order in
$v_{\rm s}$ can be derived. Taking each term in the inner products at leading order in ![]() $\epsilon$ results in
$\epsilon$ results in
The velocity gradients in (2.39), which arise from the viscous stress tensor, can be evaluated using the velocities in (2.38). As a result,
 $$\begin{gather} \mathcal{M} \frac{\partial \tilde{\gamma}}{\partial \tilde{x}} + \textit{Bq}_{\rm d} \left( \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{x} \partial \tilde{y}} \right) + \textit{Bq}_{\mathrm{sh}} \left( \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{y}^{2}} \right ) = \tilde{h} \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{ \phi})}{\partial \tilde{x}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{x}} \right) , \end{gather}$$
$$\begin{gather} \mathcal{M} \frac{\partial \tilde{\gamma}}{\partial \tilde{x}} + \textit{Bq}_{\rm d} \left( \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{x} \partial \tilde{y}} \right) + \textit{Bq}_{\mathrm{sh}} \left( \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{y}^{2}} \right ) = \tilde{h} \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{ \phi})}{\partial \tilde{x}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{x}} \right) , \end{gather}$$ $$\begin{gather}\mathcal{M} \frac{\partial \tilde{\gamma}}{\partial \tilde{y}} + \textit{Bq}_{\rm d} \left( \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{y} \partial \tilde{x}} + \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{y}^{2}} \right) + \textit{Bq}_{\mathrm{sh}} \left( \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{y}^{2}} \right ) = \tilde{h} \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{ \phi} )}{\partial \tilde{y}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{y}} \right) . \end{gather}$$
$$\begin{gather}\mathcal{M} \frac{\partial \tilde{\gamma}}{\partial \tilde{y}} + \textit{Bq}_{\rm d} \left( \frac{\partial^{2} \tilde{u}_{\rm s}}{\partial \tilde{y} \partial \tilde{x}} + \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{y}^{2}} \right) + \textit{Bq}_{\mathrm{sh}} \left( \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{x}^{2}} + \frac{\partial^{2} \tilde{v}_{\rm s}}{\partial \tilde{y}^{2}} \right ) = \tilde{h} \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{ \phi} )}{\partial \tilde{y}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{y}} \right) . \end{gather}$$
With equations for ![]() $\tilde {u}$ (2.38a) and
$\tilde {u}$ (2.38a) and ![]() $\tilde {v}$ (2.38b) at hand, the thickness evolution equation can be obtained from (2.29),
$\tilde {v}$ (2.38b) at hand, the thickness evolution equation can be obtained from (2.29),
 \begin{align} \frac{\partial \tilde{h}}{\partial \tilde{t}} &={-} \frac{\partial \tilde{u}_{\rm s}\tilde{h}}{\partial \tilde{x}} + \frac{1}{3} \frac{\partial}{\partial \tilde{x}}\left( \tilde{h}^3 \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{x}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{x}} \right) \right)\nonumber\\ &\quad - \frac{\partial \tilde{v}_{\rm s}\tilde{h}}{\partial \tilde{y}} + \frac{1}{3} \frac{\partial}{\partial \tilde{y}}\left( \tilde{h}^3 \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{y}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{y}} \right) \right) - \tilde{J}_{\rm e} . \end{align}
\begin{align} \frac{\partial \tilde{h}}{\partial \tilde{t}} &={-} \frac{\partial \tilde{u}_{\rm s}\tilde{h}}{\partial \tilde{x}} + \frac{1}{3} \frac{\partial}{\partial \tilde{x}}\left( \tilde{h}^3 \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{x}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{x}} \right) \right)\nonumber\\ &\quad - \frac{\partial \tilde{v}_{\rm s}\tilde{h}}{\partial \tilde{y}} + \frac{1}{3} \frac{\partial}{\partial \tilde{y}}\left( \tilde{h}^3 \left( \frac{\partial (\kern0.7pt \tilde{p} + \tilde{\phi})}{\partial \tilde{y}} - \varPsi \tilde{M} \frac{\partial \tilde{H}}{\partial \tilde{y}} \right) \right) - \tilde{J}_{\rm e} . \end{align}
There is no explicit ![]() $z$ dependence in the derived thickness evolution equation because of the thin film approximation. Consequently, the derived equations can be expressed compactly by introducing a dimensionless planar gradient operator defined by
$z$ dependence in the derived thickness evolution equation because of the thin film approximation. Consequently, the derived equations can be expressed compactly by introducing a dimensionless planar gradient operator defined by ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} = ({\partial }/{\partial \tilde {x}}) \boldsymbol {e}_{x} + ({\partial }/{\partial \tilde {y}}) \boldsymbol {e}_{y}$, which is a dimensionless two-dimensional version of the three-dimensional gradient operator,
$\tilde {\boldsymbol {\nabla }}_{\rm p} = ({\partial }/{\partial \tilde {x}}) \boldsymbol {e}_{x} + ({\partial }/{\partial \tilde {y}}) \boldsymbol {e}_{y}$, which is a dimensionless two-dimensional version of the three-dimensional gradient operator, ![]() $\boldsymbol {\nabla }$. We denote the dimensionless planar divergence operator by
$\boldsymbol {\nabla }$. We denote the dimensionless planar divergence operator by ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} \boldsymbol {\cdot }$ and the dimensionless planar Laplace operator (for both scalar and vector fields) by
$\tilde {\boldsymbol {\nabla }}_{\rm p} \boldsymbol {\cdot }$ and the dimensionless planar Laplace operator (for both scalar and vector fields) by ![]() $\tilde {\nabla }_{\rm p}^{2} \,$. At this stage, the centre surface of the film can be introduced such that the dividing surface is located at
$\tilde {\nabla }_{\rm p}^{2} \,$. At this stage, the centre surface of the film can be introduced such that the dividing surface is located at ![]() $z = h(x,y,t) + C(x,y)$. With the dimensionless centre surface given by
$z = h(x,y,t) + C(x,y)$. With the dimensionless centre surface given by ![]() $\tilde {C} = C / \mathcal {H}$, the equations governing the thickness evolution, written using planar operations, are
$\tilde {C} = C / \mathcal {H}$, the equations governing the thickness evolution, written using planar operations, are
Equation (2.42c) arises by writing two scalar equations, (2.40a) and (2.40b), as one vector equation, where ![]() $\tilde {\boldsymbol {V}}_{\rm s} = \tilde {u}_{\rm s} \boldsymbol {e}_{x} + \tilde {v}_{\rm s} \boldsymbol {e}_{y}$. In order for the thin film approximation to remain valid with a curved centre surface, the curvature of the centre surface,
$\tilde {\boldsymbol {V}}_{\rm s} = \tilde {u}_{\rm s} \boldsymbol {e}_{x} + \tilde {v}_{\rm s} \boldsymbol {e}_{y}$. In order for the thin film approximation to remain valid with a curved centre surface, the curvature of the centre surface, ![]() $\kappa _{\textrm{cs}}$, must be everywhere much less than the reciprocal of the characteristic thickness scale, i.e.
$\kappa _{\textrm{cs}}$, must be everywhere much less than the reciprocal of the characteristic thickness scale, i.e. ![]() $\kappa _{\textrm{cs}} \ll 1/\mathcal {H}$ (O'Brien & Schwartz Reference O'Brien and Schwartz2002).
$\kappa _{\textrm{cs}} \ll 1/\mathcal {H}$ (O'Brien & Schwartz Reference O'Brien and Schwartz2002).
The magnetisation is a function of the molar concentration of magnetite NPs, ![]() $c$, and the surface tension depends on the surface excess concentration of surfactant,
$c$, and the surface tension depends on the surface excess concentration of surfactant, ![]() $\varGamma$. Equations characterising
$\varGamma$. Equations characterising ![]() $c$ and
$c$ and ![]() $\varGamma$ are derived in §§ 2.4 and 2.5, respectively. These equations need to be solved together with (2.42a), (2.42b) and (2.42c) to determine the time evolution of film thickness.
$\varGamma$ are derived in §§ 2.4 and 2.5, respectively. These equations need to be solved together with (2.42a), (2.42b) and (2.42c) to determine the time evolution of film thickness.
2.4. Magnetite NP transport
By approximating the molar flux of magnetite NPs as the sum of fluxes due to advective transport, magnetic forcing and diffusion, the transport equation for the molar concentration of magnetite NPs, ![]() $c$, in the core liquid of a magnetic soap film can be expressed as (Pshenichnikov et al. Reference Pshenichnikov, Elfimova and Ivanov2011; Nacev et al. Reference Nacev, Komaee, Sarwar, Probst, Kim, Emmert-Buck and Shapiro2012)
$c$, in the core liquid of a magnetic soap film can be expressed as (Pshenichnikov et al. Reference Pshenichnikov, Elfimova and Ivanov2011; Nacev et al. Reference Nacev, Komaee, Sarwar, Probst, Kim, Emmert-Buck and Shapiro2012)
where ![]() $b_c$,
$b_c$, ![]() $n$ and
$n$ and ![]() $D_c$ are the mobility, number concentration and gradient diffusion coefficient of the magnetite NPs, respectively. For a dilute dispersion of magnetite NPs in a liquid, the mobility and gradient diffusion coefficient can be approximated by (Batchelor Reference Batchelor1983)
$D_c$ are the mobility, number concentration and gradient diffusion coefficient of the magnetite NPs, respectively. For a dilute dispersion of magnetite NPs in a liquid, the mobility and gradient diffusion coefficient can be approximated by (Batchelor Reference Batchelor1983)
where ![]() $\varphi$ is the volume concentration of magnetite NPs, and
$\varphi$ is the volume concentration of magnetite NPs, and ![]() $b_0$ and
$b_0$ and ![]() $D_0$ are the mobility and Brownian diffusion coefficient of an independent sphere, respectively. For a sphere of radius
$D_0$ are the mobility and Brownian diffusion coefficient of an independent sphere, respectively. For a sphere of radius ![]() $a$ (Batchelor Reference Batchelor1983),
$a$ (Batchelor Reference Batchelor1983),
where ![]() $k_{\rm B}$ is the Boltzmann constant and
$k_{\rm B}$ is the Boltzmann constant and ![]() $\mathcal {T}$ is the absolute temperature. The mobility
$\mathcal {T}$ is the absolute temperature. The mobility ![]() $b_0$ is related to
$b_0$ is related to ![]() $D_0$ through
$D_0$ through ![]() $D_0 = b_0 k_{\rm B} \mathcal {T}$ (Peskir Reference Peskir2003). Here, the mobility and gradient diffusion coefficient of magnetite NPs in a thin film have been modelled using equations derived for particles in a bulk liquid, i.e. not thin films of liquid. This is a good approximation when the film thickness dominates the size of the particles dispersed in the film (Vivek & Weeks Reference Vivek and Weeks2015; Kim et al. Reference Kim, Ribbe, Russell and Hoagland2016). For particles with size of the order of the film thickness, Prasad & Weeks (Reference Prasad and Weeks2009) found that diffusion occurred faster in soap films compared with diffusion in a bulk soap film solution. As a result, the mobility and gradient diffusion coefficient are expected to be functions of the film thickness. It is anticipated that the thickness dependence may be derived by considering the Trapeznikov approximation (Prasad & Weeks Reference Prasad and Weeks2009; Vivek & Weeks Reference Vivek and Weeks2015); however, this is not considered here as the film thickness was considerably larger than the particle dimensions throughout most of the film thinning in the experiments.
$D_0 = b_0 k_{\rm B} \mathcal {T}$ (Peskir Reference Peskir2003). Here, the mobility and gradient diffusion coefficient of magnetite NPs in a thin film have been modelled using equations derived for particles in a bulk liquid, i.e. not thin films of liquid. This is a good approximation when the film thickness dominates the size of the particles dispersed in the film (Vivek & Weeks Reference Vivek and Weeks2015; Kim et al. Reference Kim, Ribbe, Russell and Hoagland2016). For particles with size of the order of the film thickness, Prasad & Weeks (Reference Prasad and Weeks2009) found that diffusion occurred faster in soap films compared with diffusion in a bulk soap film solution. As a result, the mobility and gradient diffusion coefficient are expected to be functions of the film thickness. It is anticipated that the thickness dependence may be derived by considering the Trapeznikov approximation (Prasad & Weeks Reference Prasad and Weeks2009; Vivek & Weeks Reference Vivek and Weeks2015); however, this is not considered here as the film thickness was considerably larger than the particle dimensions throughout most of the film thinning in the experiments.
For a ferrofluid containing a dilute concentration of monodisperse magnetite NPs, the magnetisation of the ferrofluid varies with the magnetic field intensity according to (Rosensweig Reference Rosensweig2013)
where ![]() $M_{\textrm{sat}}$ is the saturation magnetisation of the ferrofluid,
$M_{\textrm{sat}}$ is the saturation magnetisation of the ferrofluid, ![]() $\mathcal {L}$ is the Langevin function (
$\mathcal {L}$ is the Langevin function (![]() $\mathcal {L}(\xi ) = \coth \xi - 1 / \xi$),
$\mathcal {L}(\xi ) = \coth \xi - 1 / \xi$), ![]() $\xi$ is the Langevin parameter and
$\xi$ is the Langevin parameter and ![]() $m$ is the magnetic dipole moment of a magnetite NP. Since
$m$ is the magnetic dipole moment of a magnetite NP. Since ![]() $M_{\textrm{sat}} = nm$,
$M_{\textrm{sat}} = nm$, ![]() $M = nm \mathcal {L}(\xi )$.
$M = nm \mathcal {L}(\xi )$.
It is evident that the magnetite NP transport equation (2.43) is three dimensional, whilst the equation governing the film thickness (2.42a) is two dimensional. The three-dimensional transport equation can be integrated over the film thickness by assuming a concentration profile over the film depth (Nierstrasz & Frens Reference Nierstrasz and Frens1999; Huybrechts, Villaret & Hervouet Reference Huybrechts, Villaret and Hervouet2010) to derive a two-dimensional transport equation for the magnetite NPs. We assumed a uniform concentration of magnetite NPs over the film depth since Brownian motion and the surfactant coating around the magnetite NPs act to uniformly disperse the NPs in the core liquid (Rosensweig Reference Rosensweig1987). Upon integrating (2.43) in ![]() $z$ and introducing the linear approximations (2.44), the magnetic force (2.5) and the magnetisation relation (2.46), the two-dimensional transport equation for the dimensionless molar concentration of magnetite NPs is
$z$ and introducing the linear approximations (2.44), the magnetic force (2.5) and the magnetisation relation (2.46), the two-dimensional transport equation for the dimensionless molar concentration of magnetite NPs is
 \begin{align} &\frac{\partial \tilde{c}}{\partial \tilde{t}} + \frac{\tilde{\boldsymbol{Q}}}{\tilde{h}} \boldsymbol{\cdot} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c} + \frac{\alpha}{Pe_c} \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} (\tilde{c} ( 1 - 6.55 \varphi_{{\rm c}} \tilde{c}) \mathcal{L} (\alpha \tilde{H}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H} )\nonumber\\ &\quad =\frac{1}{Pe_c} \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} ((1 + 1.45 \varphi_{{\rm c}} \tilde{c}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c}) , \end{align}
\begin{align} &\frac{\partial \tilde{c}}{\partial \tilde{t}} + \frac{\tilde{\boldsymbol{Q}}}{\tilde{h}} \boldsymbol{\cdot} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c} + \frac{\alpha}{Pe_c} \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} (\tilde{c} ( 1 - 6.55 \varphi_{{\rm c}} \tilde{c}) \mathcal{L} (\alpha \tilde{H}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H} )\nonumber\\ &\quad =\frac{1}{Pe_c} \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} ((1 + 1.45 \varphi_{{\rm c}} \tilde{c}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c}) , \end{align}
where ![]() $\tilde {c} = c / c_{{\rm c}}$,
$\tilde {c} = c / c_{{\rm c}}$, ![]() $\tilde {\boldsymbol {Q}} = \tilde {Q}_x \boldsymbol {e}_{x} + \tilde {Q}_y \boldsymbol {e}_{y}$,
$\tilde {\boldsymbol {Q}} = \tilde {Q}_x \boldsymbol {e}_{x} + \tilde {Q}_y \boldsymbol {e}_{y}$, ![]() $\alpha$ is a Langevin-type parameter,
$\alpha$ is a Langevin-type parameter, ![]() $Pe_c$ is a Péclet number for magnetite NP transport and
$Pe_c$ is a Péclet number for magnetite NP transport and ![]() $\varphi _{{\rm c}}$ is the volume concentration for
$\varphi _{{\rm c}}$ is the volume concentration for ![]() $c = c_{{\rm c}}$. The introduced dimensionless numbers are given by
$c = c_{{\rm c}}$. The introduced dimensionless numbers are given by
where ![]() $\mathcal {N}_{\rm A}$ is Avogadro's constant and
$\mathcal {N}_{\rm A}$ is Avogadro's constant and ![]() $\mathcal {V}_{\mathrm {p}}$ is the volume of each NP including the coating.
$\mathcal {V}_{\mathrm {p}}$ is the volume of each NP including the coating.
2.4.1. Coupling between film thickness and magnetite NP transport
In order to couple the film thickness equation (2.42a) with the magnetite NP transport equation (2.47), a relationship for ![]() $\tilde {M}$ as a function of
$\tilde {M}$ as a function of ![]() $\tilde {c}$ is needed. From
$\tilde {c}$ is needed. From ![]() $M = n m \mathcal {L} (\xi )$,
$M = n m \mathcal {L} (\xi )$,
Taking ![]() $M_{{\rm c}}$ to be the magnetisation when
$M_{{\rm c}}$ to be the magnetisation when ![]() $c = c_{{\rm c}}$ and
$c = c_{{\rm c}}$ and ![]() $H = H_{{\rm c}}$,
$H = H_{{\rm c}}$,
Injecting (2.50) into (2.49) results in the required relationship for ![]() $\tilde {M}$,
$\tilde {M}$,
2.5. Surfactant transport
The dimensionless surface tension in the pressure equation (2.42b) depends on the surfactant dynamics in the film. We assume that the surfactants stabilising each magnetic soap film are insoluble and that they form a Langmuir monolayer at each film interface with the relationship between the surface tension and surface concentration of surfactant given by the Langmuir isotherm (Manikantan & Squires Reference Manikantan and Squires2020),
where ![]() $R$ is the ideal gas constant,
$R$ is the ideal gas constant, ![]() $\varGamma _{\textrm{sat}}$ is the surface surfactant concentration for a saturated interface in units of mol m
$\varGamma _{\textrm{sat}}$ is the surface surfactant concentration for a saturated interface in units of mol m![]() $^{-2}$ and
$^{-2}$ and ![]() $\ln$ is the natural logarithm. With
$\ln$ is the natural logarithm. With ![]() $\tilde { \varGamma } = \varGamma / \varGamma _{\textrm{sat}}$, the Langmuir isotherm (2.52) in dimensionless form is
$\tilde { \varGamma } = \varGamma / \varGamma _{\textrm{sat}}$, the Langmuir isotherm (2.52) in dimensionless form is
The transport equation for the surface concentration of surfactant along a deforming surface is (Stone Reference Stone1990)
where ![]() $D_{\rm s}$ is the surface diffusion coefficient for surfactant transport and
$D_{\rm s}$ is the surface diffusion coefficient for surfactant transport and ![]() $\nabla _{\rm s}^{2}$ is the surface Laplace operator. This equation assumes that there is no transport of surfactant between the core liquid and the surface and that the diffusive flux of surfactant along the surface is governed by
$\nabla _{\rm s}^{2}$ is the surface Laplace operator. This equation assumes that there is no transport of surfactant between the core liquid and the surface and that the diffusive flux of surfactant along the surface is governed by
with ![]() $D_{\rm s}$ uniform over the surface. This diffusion relation is not consistent with the Langmuir isotherm; therefore, the following diffusive flux relation that is consistent with the Langmuir isotherm was used (Manikantan & Squires Reference Manikantan and Squires2020):
$D_{\rm s}$ uniform over the surface. This diffusion relation is not consistent with the Langmuir isotherm; therefore, the following diffusive flux relation that is consistent with the Langmuir isotherm was used (Manikantan & Squires Reference Manikantan and Squires2020):
Here ![]() $D_{\rm s}$ was assumed to be uniform over the surface and constant in time. The partial time derivative in the surfactant transport equation (2.54) should be interpreted as the change in
$D_{\rm s}$ was assumed to be uniform over the surface and constant in time. The partial time derivative in the surfactant transport equation (2.54) should be interpreted as the change in ![]() $\varGamma$ when following the interface in a direction normal to the original interface (Wong, Rumschitzki & Maldarelli Reference Wong, Rumschitzki and Maldarelli1996; Pereira et al. Reference Pereira, Trevelyan, Thiele and Kalliadasis2007). Each position on the dividing surface can be specified by two parameters known as the surface coordinates (Slattery et al. Reference Slattery, Sagis and Oh2007), and it is easier to work in terms of partial time derivatives when following the evolution of the interface at fixed surface coordinates. We can conveniently use
$\varGamma$ when following the interface in a direction normal to the original interface (Wong, Rumschitzki & Maldarelli Reference Wong, Rumschitzki and Maldarelli1996; Pereira et al. Reference Pereira, Trevelyan, Thiele and Kalliadasis2007). Each position on the dividing surface can be specified by two parameters known as the surface coordinates (Slattery et al. Reference Slattery, Sagis and Oh2007), and it is easier to work in terms of partial time derivatives when following the evolution of the interface at fixed surface coordinates. We can conveniently use ![]() $x$ and
$x$ and ![]() $y$ as the surface coordinates since the position vector of any point on the dividing surface is
$y$ as the surface coordinates since the position vector of any point on the dividing surface is
Wong et al. (Reference Wong, Rumschitzki and Maldarelli1996) and Cermelli, Fried & Gurtin (Reference Cermelli, Fried and Gurtin2005) provide a relation for the partial time derivative present in the transport equation (2.54) in terms of the partial time derivative when keeping the surface coordinates fixed, which we denote by ![]() $(\frac {\partial \varGamma }{\partial t})_{\circ }$,
$(\frac {\partial \varGamma }{\partial t})_{\circ }$,
where ![]() $\boldsymbol {U}_{{\rm s}}$ is the rate of change of spatial position following a point on the surface with fixed surface coordinates, i.e.
$\boldsymbol {U}_{{\rm s}}$ is the rate of change of spatial position following a point on the surface with fixed surface coordinates, i.e.
Following from (2.57), ![]() $\boldsymbol {U}_{\rm s} = (\partial h/\partial t) \boldsymbol {e}_{z}$. With (2.56) and (2.58), the surfactant transport equation (2.54) becomes
$\boldsymbol {U}_{\rm s} = (\partial h/\partial t) \boldsymbol {e}_{z}$. With (2.56) and (2.58), the surfactant transport equation (2.54) becomes
 \begin{align} &\left(\frac{\partial
\varGamma}{\partial t}\right)_{{\circ}} -
\boldsymbol{U}_{\rm s} \boldsymbol{\cdot}
\boldsymbol{\nabla}_{\rm s} \varGamma +
\boldsymbol{\nabla}_{\rm s} \boldsymbol{\cdot} (\varGamma
\boldsymbol{\mathsf{P}}_{\rm s} \boldsymbol{\cdot}
\boldsymbol{V}_{\rm s}) + \varGamma (\boldsymbol{\nabla}_{\rm s}
\boldsymbol{\cdot} \boldsymbol{n})(\boldsymbol{V}_{\rm s}
\boldsymbol{\cdot} \boldsymbol{n}) \nonumber\\ &\quad =
D_{\rm s} \boldsymbol{\nabla}_{\rm s} \boldsymbol{\cdot}
\left(\frac{\varGamma_{\textrm{sat}}}{\varGamma_{\textrm{sat}}-\varGamma}
\boldsymbol{\nabla}_{\rm s} \varGamma \right) ,
\end{align}
\begin{align} &\left(\frac{\partial
\varGamma}{\partial t}\right)_{{\circ}} -
\boldsymbol{U}_{\rm s} \boldsymbol{\cdot}
\boldsymbol{\nabla}_{\rm s} \varGamma +
\boldsymbol{\nabla}_{\rm s} \boldsymbol{\cdot} (\varGamma
\boldsymbol{\mathsf{P}}_{\rm s} \boldsymbol{\cdot}
\boldsymbol{V}_{\rm s}) + \varGamma (\boldsymbol{\nabla}_{\rm s}
\boldsymbol{\cdot} \boldsymbol{n})(\boldsymbol{V}_{\rm s}
\boldsymbol{\cdot} \boldsymbol{n}) \nonumber\\ &\quad =
D_{\rm s} \boldsymbol{\nabla}_{\rm s} \boldsymbol{\cdot}
\left(\frac{\varGamma_{\textrm{sat}}}{\varGamma_{\textrm{sat}}-\varGamma}
\boldsymbol{\nabla}_{\rm s} \varGamma \right) ,
\end{align}
which in dimensionless form and at leading order in ![]() $\epsilon$ is
$\epsilon$ is
 \begin{equation} \left(\frac{\partial \tilde{\varGamma}}{\partial \tilde{t}}\right)_{{\circ}} + \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} ( \tilde{\boldsymbol{V}}_{\rm s} \tilde{\varGamma} ) = \frac{1}{Pe_{\rm s}} \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} \left( \frac{1}{1 - \tilde{ \varGamma}} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{ \varGamma} \right) , \end{equation}
\begin{equation} \left(\frac{\partial \tilde{\varGamma}}{\partial \tilde{t}}\right)_{{\circ}} + \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} ( \tilde{\boldsymbol{V}}_{\rm s} \tilde{\varGamma} ) = \frac{1}{Pe_{\rm s}} \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} \left( \frac{1}{1 - \tilde{ \varGamma}} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{ \varGamma} \right) , \end{equation}
where ![]() $Pe_{\rm s}$ is the Péclet number for surfactant transport along the dividing surface. This Péclet number is given by
$Pe_{\rm s}$ is the Péclet number for surfactant transport along the dividing surface. This Péclet number is given by
2.6. Closures
In order to solve for the film thickness, closures are needed for the evaporation rate and disjoining pressure.
2.6.1. Evaporation rate
In the simplest case, soap films can be simulated assuming a constant and uniform rate of evaporation (Huang et al. Reference Huang, Iseringhausen, Kneiphof, Qu, Jiang and Hullin2020; Ishida et al. Reference Ishida, Synak, Narita, Hachisuka and Wojtan2020; Pasquet et al. Reference Pasquet, Boulogne, Sant-Anna, Restagno and Rio2022). A more accurate treatment of evaporation involves solving the energy balance equation in the core liquid and the jump energy balance equation at the dividing surface and introducing a constitutive relation between the mass flux due to evaporation and the interface temperature (Burelbach et al. Reference Burelbach, Bankoff and Davis1988; Sultan, Boudaoud & Amar Reference Sultan, Boudaoud and Amar2005). To isolate the effects of drainage phenomena, all simulations were conducted without evaporation, i.e. ![]() $\tilde {J}_{{\rm e}} = 0$. We leave it as an area of future work to couple the system of equations introduced in the present contribution with the energy balance equations.
$\tilde {J}_{{\rm e}} = 0$. We leave it as an area of future work to couple the system of equations introduced in the present contribution with the energy balance equations.
2.6.2. Disjoining pressure
The Derjaguin–Landau–Verwey–Overbeek (DLVO) theory was used for the disjoining pressure in this study (see Ninham Reference Ninham1999 for a list of assumptions inherent in DLVO theory). With the DLVO theory, the disjoining pressure is expressed as the sum of attractive van der Waals forces and repulsive electric double layer forces. Under the assumption of identically charged planar surfaces with a small and constant surface potential, the disjoining pressure is given by the relation (Bergeron Reference Bergeron1999; Matsubara et al. Reference Matsubara, Kimura, Miyao, Shin and Ikeda2021; Agmo Hernández Reference Agmo Hernández2023)
where ![]() $A$ is the Hamaker constant,
$A$ is the Hamaker constant, ![]() $B$ is a parameter that depends on the interface potential and
$B$ is a parameter that depends on the interface potential and ![]() $\zeta ^{-1}$ is the Debye length. In dimensionless form, (2.63) is
$\zeta ^{-1}$ is the Debye length. In dimensionless form, (2.63) is
where the introduced dimensionless numbers are
We used constant values for ![]() $\mathcal {A}$,
$\mathcal {A}$, ![]() $\mathcal {B}$ and
$\mathcal {B}$ and ![]() $\mathcal {D}$ throughout the simulations, which does not account for the spatiotemporally varying interfacial surfactant concentration. Note that DLVO theory does not have general applicability, for example, it would not be effective at predicting the equilibrium thickness of Newton black films (Ochoa et al. Reference Ochoa, Gao, Srivastava and Sharma2021). Additional interactions, such as steric forces or solvation forces, may need to be accounted for to more accurately represent the disjoining pressure for films of interest (Bergeron Reference Bergeron1999).
$\mathcal {D}$ throughout the simulations, which does not account for the spatiotemporally varying interfacial surfactant concentration. Note that DLVO theory does not have general applicability, for example, it would not be effective at predicting the equilibrium thickness of Newton black films (Ochoa et al. Reference Ochoa, Gao, Srivastava and Sharma2021). Additional interactions, such as steric forces or solvation forces, may need to be accounted for to more accurately represent the disjoining pressure for films of interest (Bergeron Reference Bergeron1999).
2.7. Solving
The thickness field is governed by the system of coupled partial differential equations (PDEs) defined by (2.42a–c), (2.47) and (2.61), where the variables that must be solved for are ![]() $(\tilde {h}, \tilde {p}, \tilde { \boldsymbol {V}}_{{\rm s}}, \tilde {c}, \tilde { \varGamma })$. The Galerkin finite element method was used to solve this coupled system with the addition of suitable initial and boundary conditions and the relations for the magnetisation (2.51), surface tension (2.53) and disjoining pressure (2.64). With (2.42b) in (2.42a), the thickness evolution equation is a nonlinear fourth-order parabolic equation (Liu, Peco & Dolbow Reference Liu, Peco and Dolbow2019). A fourth-order PDE of this type can be solved with mixed finite element methods (Wells, Kuhl & Garikipati Reference Wells, Kuhl and Garikipati2006; Liu et al. Reference Liu, Peco and Dolbow2019; Keita, Beljadid & Bourgault Reference Keita, Beljadid and Bourgault2021), which involve solving the fourth-order equation as a system of two second-order equations. This allows for the use of standard Lagrange finite element basis functions to approximate the unknowns. It was natural to solve for
$(\tilde {h}, \tilde {p}, \tilde { \boldsymbol {V}}_{{\rm s}}, \tilde {c}, \tilde { \varGamma })$. The Galerkin finite element method was used to solve this coupled system with the addition of suitable initial and boundary conditions and the relations for the magnetisation (2.51), surface tension (2.53) and disjoining pressure (2.64). With (2.42b) in (2.42a), the thickness evolution equation is a nonlinear fourth-order parabolic equation (Liu, Peco & Dolbow Reference Liu, Peco and Dolbow2019). A fourth-order PDE of this type can be solved with mixed finite element methods (Wells, Kuhl & Garikipati Reference Wells, Kuhl and Garikipati2006; Liu et al. Reference Liu, Peco and Dolbow2019; Keita, Beljadid & Bourgault Reference Keita, Beljadid and Bourgault2021), which involve solving the fourth-order equation as a system of two second-order equations. This allows for the use of standard Lagrange finite element basis functions to approximate the unknowns. It was natural to solve for ![]() $\tilde {p} + \tilde { \phi }$ (2.42b) as one of the second-order equations.
$\tilde {p} + \tilde { \phi }$ (2.42b) as one of the second-order equations.
Uniform initial conditions were used for each of the five variables. In all simulations, the initial pressure was set to 0 and the initial surface velocity was set to ![]() $\boldsymbol {0}$. The initial conditions for
$\boldsymbol {0}$. The initial conditions for ![]() $\tilde {h}$,
$\tilde {h}$, ![]() $\tilde {c}$ and
$\tilde {c}$ and ![]() $\tilde { \varGamma }$, which we denote by
$\tilde { \varGamma }$, which we denote by ![]() $\tilde {h}_{\rm i}$,
$\tilde {h}_{\rm i}$, ![]() $\tilde {c}_{\rm i}$ and
$\tilde {c}_{\rm i}$ and ![]() $\tilde { \varGamma }_{\rm i}$, are given in table 1 for each simulation.
$\tilde { \varGamma }_{\rm i}$, are given in table 1 for each simulation.
Table 1. The dimensionless numbers used for the governing equations, boundary conditions and initial conditions are provided for the simulations presented in each section. The number of cells, ![]() $N_{\textrm{cell}}$, used to discretise the domain to the nearest 100 cells is also provided. Section 3.1(i) refers to the immobile soap film and § 3.1(p) refers to the partially mobile soap films simulated in § 3.1. Section 3.2(u) refers to the simulated magnetic soap films with a uniform concentration of magnetite NPs for two boundary conditions, and § 3.2(t) refers to the same but when considering the transport of magnetite NPs. The
$N_{\textrm{cell}}$, used to discretise the domain to the nearest 100 cells is also provided. Section 3.1(i) refers to the immobile soap film and § 3.1(p) refers to the partially mobile soap films simulated in § 3.1. Section 3.2(u) refers to the simulated magnetic soap films with a uniform concentration of magnetite NPs for two boundary conditions, and § 3.2(t) refers to the same but when considering the transport of magnetite NPs. The ![]() $\leftarrow$ symbol indicates that the simulation parameter was the same as the value for the simulation in the column to the left, e.g. the same value was used for the capillary number,
$\leftarrow$ symbol indicates that the simulation parameter was the same as the value for the simulation in the column to the left, e.g. the same value was used for the capillary number, ![]() $\mathcal {C}$, for all simulations. A hyphen symbolises that a parameter does not affect the results of a simulation, e.g. the value of
$\mathcal {C}$, for all simulations. A hyphen symbolises that a parameter does not affect the results of a simulation, e.g. the value of ![]() $\varPsi$ has no effect when there are no magnetite NPs in the film (
$\varPsi$ has no effect when there are no magnetite NPs in the film (![]() $\tilde {c}_{\rm i} = 0.0$).
$\tilde {c}_{\rm i} = 0.0$).

Five boundary conditions are needed on ![]() $\partial \varOmega$, one corresponding to each of the five second-order PDEs. As discussed in the introduction, a net flow of liquid is expected between the meniscus and the thin film due to capillary suction and marginal regeneration; therefore, we did not employ a no-flux boundary condition. Instead, since a larger force acts on thicker film due to this suction compared with thinner film (Overbeek Reference Overbeek1960; Mysels Reference Mysels1968), we imposed a boundary condition relating the flux of liquid out of the thin film due to capillary suction to the local film thickness at the boundary,
$\partial \varOmega$, one corresponding to each of the five second-order PDEs. As discussed in the introduction, a net flow of liquid is expected between the meniscus and the thin film due to capillary suction and marginal regeneration; therefore, we did not employ a no-flux boundary condition. Instead, since a larger force acts on thicker film due to this suction compared with thinner film (Overbeek Reference Overbeek1960; Mysels Reference Mysels1968), we imposed a boundary condition relating the flux of liquid out of the thin film due to capillary suction to the local film thickness at the boundary,
where ![]() $\mathcal {P}$ governs the strength of capillary suction and
$\mathcal {P}$ governs the strength of capillary suction and ![]() $\tilde {p}_{\rm c}$ is the dimensionless capillary pressure. It is unknown at present how the suction strength depends on the applied magnetic field due to the influence of the applied magnetic field on the meniscus shape (Rosensweig et al. Reference Rosensweig, Elborai, Lee and Zahn2005; Singh et al. Reference Singh, Singh and Bhaumik2024); this could be an interesting area for future research. For some of the simulations in which a magnetic field was applied, we also investigated the boundary condition
$\tilde {p}_{\rm c}$ is the dimensionless capillary pressure. It is unknown at present how the suction strength depends on the applied magnetic field due to the influence of the applied magnetic field on the meniscus shape (Rosensweig et al. Reference Rosensweig, Elborai, Lee and Zahn2005; Singh et al. Reference Singh, Singh and Bhaumik2024); this could be an interesting area for future research. For some of the simulations in which a magnetic field was applied, we also investigated the boundary condition
which imposes a limit on the drainage flux of core liquid out of the thin film (without disjoining pressure contributions), determined by the parameter ![]() $\mathcal {Q}$.
$\mathcal {Q}$.
A Neumann boundary condition was used for the film thickness to allow the film thickness to change with time at the boundary of the thin film. The Neumann condition sets ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {h} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$ on
$\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {h} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$ on ![]() $\partial \varOmega$, which we denote by
$\partial \varOmega$, which we denote by ![]() ${\partial \tilde {h}}/{\partial n_{\rm d}}$.
${\partial \tilde {h}}/{\partial n_{\rm d}}$.
The divergence of the tensor ![]() $\textit {Bq}_{\rm d} (\tilde {\boldsymbol {\nabla }}_{\rm p} \boldsymbol {\cdot } \tilde {\boldsymbol {V}}_{\rm s}) \boldsymbol{\mathsf{I}} + \textit {Bq}_{\mathrm {sh}} \tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {\boldsymbol {V}}_{\rm s}$ appears in (2.42c), and the weak variational form features this tensor operating on
$\textit {Bq}_{\rm d} (\tilde {\boldsymbol {\nabla }}_{\rm p} \boldsymbol {\cdot } \tilde {\boldsymbol {V}}_{\rm s}) \boldsymbol{\mathsf{I}} + \textit {Bq}_{\mathrm {sh}} \tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {\boldsymbol {V}}_{\rm s}$ appears in (2.42c), and the weak variational form features this tensor operating on ![]() $\boldsymbol {n}_{\rm d}$. We chose to adopt the natural boundary condition
$\boldsymbol {n}_{\rm d}$. We chose to adopt the natural boundary condition
A number of Neumann and Dirichlet boundary conditions were investigated for ![]() $\tilde {c}$; however, the most physically consistent behaviour was observed with the boundary condition
$\tilde {c}$; however, the most physically consistent behaviour was observed with the boundary condition
which is a balance of the flux of ![]() $\tilde {c}$ out of the thin film between magnetic forcing and diffusion. With this boundary condition, the concentration of magnetite NPs averaged over the thin film can change with time due to the advective flux in (2.47).
$\tilde {c}$ out of the thin film between magnetic forcing and diffusion. With this boundary condition, the concentration of magnetite NPs averaged over the thin film can change with time due to the advective flux in (2.47).
Nierstrasz & Frens (Reference Nierstrasz and Frens1999) argued that with marginal regeneration, the surfactant that flows out of the thin film during drainage is replaced by an equal amount of surfactant from saturated patches of fluid that are extracted from the film boundary. Consequently, we used a boundary condition that keeps the amount of surfactant covering the thin film constant in time,
which is a no-flux surfactant boundary condition.
We use the following compact notation to express the problem of finding the time evolution of film thickness in weak form (Langtangen & Logg Reference Langtangen and Logg2017):
The mixed weak form of the problem, with the boundary conditions inserted into the surface integral terms and the initial conditions not repeated here for brevity, is to find ![]() $(\tilde {h}, \tilde {p}, \tilde { \boldsymbol {V}}_{{\rm s}}, \tilde {c}, \tilde { \varGamma }) \in K^{(0)} \times {K^{(1)}} \times {{ \boldsymbol {K}}^{(2)}} \times {K^{(3)}} \times {K^{(4)}}$ such that
$(\tilde {h}, \tilde {p}, \tilde { \boldsymbol {V}}_{{\rm s}}, \tilde {c}, \tilde { \varGamma }) \in K^{(0)} \times {K^{(1)}} \times {{ \boldsymbol {K}}^{(2)}} \times {K^{(3)}} \times {K^{(4)}}$ such that
 \begin{align} &\left\langle \frac{\partial \tilde{h}}{\partial \tilde{t}}, {k^{(0)}} \right\rangle + \langle \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} ( \tilde{\boldsymbol{V}}_{\rm s} \tilde{h} ), {k^{(0)}} \rangle + \frac 13 \langle \tilde{h}^3 \tilde{\boldsymbol{\nabla}}_{\rm p} (\kern0.7pt \tilde{p} + \tilde{ \phi}), \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(0)}} \rangle + \langle \tilde{J}_{\rm e}, {k^{(0)}} \rangle \nonumber\\ &\quad + \frac 13 \varPsi \langle \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} (\tilde{h}^3 \tilde{M} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H}), {k^{(0)}} \rangle - \frac 13 \epsilon \mathcal{G} \langle \tilde{h}^3 \tilde{\boldsymbol{\nabla}}_{\rm p} (\tilde{h} + \tilde{C}) \boldsymbol{\cdot} \boldsymbol{n}_{\rm d}, {k^{(0)}} \rangle_{\partial\varOmega} \nonumber\\ &\quad + \langle \mathcal{P} \tilde{h}^3, {k^{(0)}} \rangle_{\partial\varOmega} + \frac{1}{3} \langle \tilde{h}^3 \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{\varPi} \boldsymbol{\cdot} \boldsymbol{n}_{\rm d}, {k^{(0)}} \rangle_{\partial\varOmega} = 0 \quad \forall {k^{(0)}} \in {K^{(0)}} , \end{align}
\begin{align} &\left\langle \frac{\partial \tilde{h}}{\partial \tilde{t}}, {k^{(0)}} \right\rangle + \langle \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} ( \tilde{\boldsymbol{V}}_{\rm s} \tilde{h} ), {k^{(0)}} \rangle + \frac 13 \langle \tilde{h}^3 \tilde{\boldsymbol{\nabla}}_{\rm p} (\kern0.7pt \tilde{p} + \tilde{ \phi}), \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(0)}} \rangle + \langle \tilde{J}_{\rm e}, {k^{(0)}} \rangle \nonumber\\ &\quad + \frac 13 \varPsi \langle \tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} (\tilde{h}^3 \tilde{M} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H}), {k^{(0)}} \rangle - \frac 13 \epsilon \mathcal{G} \langle \tilde{h}^3 \tilde{\boldsymbol{\nabla}}_{\rm p} (\tilde{h} + \tilde{C}) \boldsymbol{\cdot} \boldsymbol{n}_{\rm d}, {k^{(0)}} \rangle_{\partial\varOmega} \nonumber\\ &\quad + \langle \mathcal{P} \tilde{h}^3, {k^{(0)}} \rangle_{\partial\varOmega} + \frac{1}{3} \langle \tilde{h}^3 \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{\varPi} \boldsymbol{\cdot} \boldsymbol{n}_{\rm d}, {k^{(0)}} \rangle_{\partial\varOmega} = 0 \quad \forall {k^{(0)}} \in {K^{(0)}} , \end{align} \begin{align} &\langle \tilde{p} + \tilde{ \phi}, {k^{(1)}} \rangle - \epsilon \mathcal{G} \langle \tilde{h} + \tilde{C}, {k^{(1)}} \rangle - \left\langle \left(\epsilon^2 \mathcal{M} \tilde{ \gamma} + \frac{\epsilon^3}{\mathcal{C}}\right) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{h} , \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(1)}} \right\rangle\nonumber\\ &\quad + \langle \tilde{ \varPi}, {k^{(1)}} \rangle + \left\langle \left(\epsilon^2 \mathcal{M} \tilde{ \gamma} + \frac{\epsilon^3}{\mathcal{C}}\right) \frac{\partial \tilde{h}}{\partial n_{\rm d}}, {k^{(1)}} \right\rangle_{\partial\varOmega} = 0 \quad \forall {k^{(1)}} \in {K^{(1)}} , \end{align}
\begin{align} &\langle \tilde{p} + \tilde{ \phi}, {k^{(1)}} \rangle - \epsilon \mathcal{G} \langle \tilde{h} + \tilde{C}, {k^{(1)}} \rangle - \left\langle \left(\epsilon^2 \mathcal{M} \tilde{ \gamma} + \frac{\epsilon^3}{\mathcal{C}}\right) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{h} , \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(1)}} \right\rangle\nonumber\\ &\quad + \langle \tilde{ \varPi}, {k^{(1)}} \rangle + \left\langle \left(\epsilon^2 \mathcal{M} \tilde{ \gamma} + \frac{\epsilon^3}{\mathcal{C}}\right) \frac{\partial \tilde{h}}{\partial n_{\rm d}}, {k^{(1)}} \right\rangle_{\partial\varOmega} = 0 \quad \forall {k^{(1)}} \in {K^{(1)}} , \end{align} \begin{align} &\mathcal{M} \langle \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{ \gamma}, {{ \boldsymbol {k}}^{(2)}} \rangle - \int_{\varOmega} (\textit{Bq}_{\rm d} (\tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} \tilde{\boldsymbol{V}}_{\rm s}) \boldsymbol{\mathsf{I}} + \textit{Bq}_{\mathrm{sh}} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{\boldsymbol{V}}_{\rm s}) \boldsymbol{:} \tilde{\boldsymbol{\nabla}}_{\rm p} {{ \boldsymbol {k}}^{(2)}} \, \mathrm{d}\varOmega\nonumber\\ &\quad- \langle \tilde{h} (\tilde{\boldsymbol{\nabla}}_{\rm p} (\kern0.7pt \tilde{p} + \tilde{ \phi}) - \varPsi \tilde{M} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H}), {{ \boldsymbol {k}}^{(2)}} \rangle = 0 \quad \forall {{ \boldsymbol {k}}^{(2)}} \in {{ \boldsymbol {K}}^{2}} , \end{align}
\begin{align} &\mathcal{M} \langle \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{ \gamma}, {{ \boldsymbol {k}}^{(2)}} \rangle - \int_{\varOmega} (\textit{Bq}_{\rm d} (\tilde{\boldsymbol{\nabla}}_{\rm p} \boldsymbol{\cdot} \tilde{\boldsymbol{V}}_{\rm s}) \boldsymbol{\mathsf{I}} + \textit{Bq}_{\mathrm{sh}} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{\boldsymbol{V}}_{\rm s}) \boldsymbol{:} \tilde{\boldsymbol{\nabla}}_{\rm p} {{ \boldsymbol {k}}^{(2)}} \, \mathrm{d}\varOmega\nonumber\\ &\quad- \langle \tilde{h} (\tilde{\boldsymbol{\nabla}}_{\rm p} (\kern0.7pt \tilde{p} + \tilde{ \phi}) - \varPsi \tilde{M} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H}), {{ \boldsymbol {k}}^{(2)}} \rangle = 0 \quad \forall {{ \boldsymbol {k}}^{(2)}} \in {{ \boldsymbol {K}}^{2}} , \end{align} \begin{align} &\left\langle \frac{\partial \tilde{c}}{\partial \tilde{t}}, {k^{(3)}} \right\rangle + \left\langle \frac{\tilde{\boldsymbol{Q}}}{\tilde{h}} \boldsymbol{\cdot} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c}, {k^{(3)}} \right\rangle + \frac{1}{Pe_c} \langle (1 + 1.45 \varphi_{{\rm c}} \tilde{c}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c}, \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(3)}} \rangle \nonumber\\ &\quad - \frac{\alpha}{Pe_c} \langle \tilde{c} ( 1 - 6.55 \varphi_{{\rm c}} \tilde{c}) \mathcal{L} (\alpha \tilde{H}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H} , \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(3)}} \rangle = 0 \quad \forall {k^{(3)}} \in {K^{(3)}} , \end{align}
\begin{align} &\left\langle \frac{\partial \tilde{c}}{\partial \tilde{t}}, {k^{(3)}} \right\rangle + \left\langle \frac{\tilde{\boldsymbol{Q}}}{\tilde{h}} \boldsymbol{\cdot} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c}, {k^{(3)}} \right\rangle + \frac{1}{Pe_c} \langle (1 + 1.45 \varphi_{{\rm c}} \tilde{c}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{c}, \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(3)}} \rangle \nonumber\\ &\quad - \frac{\alpha}{Pe_c} \langle \tilde{c} ( 1 - 6.55 \varphi_{{\rm c}} \tilde{c}) \mathcal{L} (\alpha \tilde{H}) \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{H} , \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(3)}} \rangle = 0 \quad \forall {k^{(3)}} \in {K^{(3)}} , \end{align} \begin{align} &\left\langle \left(\frac{\partial \tilde{\varGamma}}{\partial \tilde{t}}\right)_{{\circ}}, {k^{(4)}} \right\rangle - \langle \tilde{\varGamma} \tilde{\boldsymbol{V}}_{\rm s}, \tilde{\boldsymbol{\nabla}}_{\rm p}{k^{(4)}} \rangle + \frac{1}{Pe_{\rm s}} \left\langle \frac{1}{1 - \tilde{ \varGamma}} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{ \varGamma}, \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(4)}} \right\rangle = 0 \quad \forall {k^{(4)}} \in {K^{(4)}} , \end{align}
\begin{align} &\left\langle \left(\frac{\partial \tilde{\varGamma}}{\partial \tilde{t}}\right)_{{\circ}}, {k^{(4)}} \right\rangle - \langle \tilde{\varGamma} \tilde{\boldsymbol{V}}_{\rm s}, \tilde{\boldsymbol{\nabla}}_{\rm p}{k^{(4)}} \rangle + \frac{1}{Pe_{\rm s}} \left\langle \frac{1}{1 - \tilde{ \varGamma}} \tilde{\boldsymbol{\nabla}}_{\rm p} \tilde{ \varGamma}, \tilde{\boldsymbol{\nabla}}_{\rm p} {k^{(4)}} \right\rangle = 0 \quad \forall {k^{(4)}} \in {K^{(4)}} , \end{align}
where ![]() $\boldsymbol {:}$ is the Frobenius inner product,
$\boldsymbol {:}$ is the Frobenius inner product, ![]() $k^{(i)}$ are test functions and
$k^{(i)}$ are test functions and ![]() $K^{(i)}$ are suitable infinite-dimensional function spaces containing the exact solution to the problem. Since the centre surface was assumed to be of uniform curvature,
$K^{(i)}$ are suitable infinite-dimensional function spaces containing the exact solution to the problem. Since the centre surface was assumed to be of uniform curvature, ![]() $\tilde {\nabla }_{\rm p}^{2} \tilde {C}$ was set to 0 in (2.72b).
$\tilde {\nabla }_{\rm p}^{2} \tilde {C}$ was set to 0 in (2.72b).
The FEniCSx project, which comprises Basix (Scroggs et al. Reference Scroggs, Baratta, Richardson and Wells2022a,Reference Scroggs, Dokken, Richardson and Wellsb), UFL (Alnæs et al. Reference Alnæs, Logg, Ølgaard, Rognes and Wells2014), FFCx and DOLFINx (Baratta et al. Reference Baratta, Dean, Dokken, Habera, Hale, Richardson, Rognes, Scroggs, Sime and Wells2023), was used to find approximate solutions to the variational problem (2.72). All time derivatives were discretised using the backward Euler scheme with a time step of ![]() $\Delta \tilde {t} = 0.001$, except where otherwise noted, and the finite element method was used at each time step to solve the time-discrete system of PDEs on a triangulation of the domain with linear Lagrange basis functions used to approximate all variables being solved for. The triangulation was created using Gmsh (Geuzaine & Remacle Reference Geuzaine and Remacle2009), with increased refinement from the centre to the circumference of the circular domain to better resolve large gradients in
$\Delta \tilde {t} = 0.001$, except where otherwise noted, and the finite element method was used at each time step to solve the time-discrete system of PDEs on a triangulation of the domain with linear Lagrange basis functions used to approximate all variables being solved for. The triangulation was created using Gmsh (Geuzaine & Remacle Reference Geuzaine and Remacle2009), with increased refinement from the centre to the circumference of the circular domain to better resolve large gradients in ![]() $\tilde {h}$ and
$\tilde {h}$ and ![]() $\tilde { \varGamma }$ near the domain boundary. Table 1 presents the number of cells,
$\tilde { \varGamma }$ near the domain boundary. Table 1 presents the number of cells, ![]() $N_{\textrm{cell}}$, used in each simulation. The number of cells used for each simulation was chosen by investigating increasing numbers of cells until the boundary conditions were enforced with sufficient accuracy and the average thickness over time had converged with the number of cells. Newton's method, through an interface from DOLFINx to PETSc's Newton solver (Dalcin et al. Reference Dalcin, Paz, Kler and Cosimo2011), was used to solve the system of nonlinear algebraic equations arising after implicit temporal discretisation and finite element spatial discretisation. Convergence criteria based on the residual were employed with tolerances for the absolute and relative residuals set to
$N_{\textrm{cell}}$, used in each simulation. The number of cells used for each simulation was chosen by investigating increasing numbers of cells until the boundary conditions were enforced with sufficient accuracy and the average thickness over time had converged with the number of cells. Newton's method, through an interface from DOLFINx to PETSc's Newton solver (Dalcin et al. Reference Dalcin, Paz, Kler and Cosimo2011), was used to solve the system of nonlinear algebraic equations arising after implicit temporal discretisation and finite element spatial discretisation. Convergence criteria based on the residual were employed with tolerances for the absolute and relative residuals set to ![]() $10^{-10}$. The multifrontal massively parallel sparse direct solver (MUMPS) with LU factorisation (Amestoy et al. Reference Amestoy, Duff, L'Excellent and Koster2000) was used to solve the linear system in each Newton iteration. All simulations were run in parallel on 16 processors (Intel Xeon Silver 4216 processor
$10^{-10}$. The multifrontal massively parallel sparse direct solver (MUMPS) with LU factorisation (Amestoy et al. Reference Amestoy, Duff, L'Excellent and Koster2000) was used to solve the linear system in each Newton iteration. All simulations were run in parallel on 16 processors (Intel Xeon Silver 4216 processor ![]() $-$2.10 GHz base frequency) using the message passing interface (Dalcin & Fang Reference Dalcin and Fang2021). For the simulations presented in § 3.4 (
$-$2.10 GHz base frequency) using the message passing interface (Dalcin & Fang Reference Dalcin and Fang2021). For the simulations presented in § 3.4 (![]() $N_{\textrm{cell}} = 195\,400$,
$N_{\textrm{cell}} = 195\,400$, ![]() $\Delta \tilde {t} = 0.001$,
$\Delta \tilde {t} = 0.001$, ![]() $\tilde {t} \in [0, 0.5]$), the simulation time was approximately 2 h.
$\tilde {t} \in [0, 0.5]$), the simulation time was approximately 2 h.
The dimensionless numbers that were used for each simulation are provided in table 1. The properties and scales in table 2 of Appendix B, or values similar to those provided, were used to calculate many of the dimensionless numbers in table 1. The characteristic length scale was chosen as 2 mm on the basis that the strength of capillary suction is determined by the meniscus curvature and the characteristic size of the meniscus is given by the capillary length (Gennes et al. Reference Gennes, Brochard-Wyart and Quéré2004; Berg, Adelizzi & Troian Reference Berg, Adelizzi and Troian2005), which is ![]() $\sqrt {{\gamma }/(\rho g)} \approx 2$ mm. Furthermore, the velocity scale
$\sqrt {{\gamma }/(\rho g)} \approx 2$ mm. Furthermore, the velocity scale ![]() $U = 4\times 10^{-6}$ m s
$U = 4\times 10^{-6}$ m s![]() $^{-1}$ was found by setting the capillary number to
$^{-1}$ was found by setting the capillary number to ![]() $\mathcal {C} = 10^{-7}$ so that capillary effects enter the problem at leading order, i.e.
$\mathcal {C} = 10^{-7}$ so that capillary effects enter the problem at leading order, i.e. ![]() $\epsilon ^3 / \mathcal {C} \sim 1$.
$\epsilon ^3 / \mathcal {C} \sim 1$.
2.8. Validation
Appendix C presents the model derived in this study adapted to free vertical magnetic soap films. Given that the model in Appendix C simplifies to the model in Moulton & Pelesko (Reference Moulton and Pelesko2010) under several assumptions, we can validate our numerical implementation of the model derived in the present study by comparison with the simulation results in Moulton & Pelesko (Reference Moulton and Pelesko2010). With the assumptions used in Moulton & Pelesko (Reference Moulton and Pelesko2010), which are immobile interfaces, uniform surface tension, a linear relationship between the film magnetisation and the magnetic field intensity (![]() $\tilde {M} = \tilde {H}$), no disjoining pressure effects and no evaporation, the model detailed in Appendix C simplifies to
$\tilde {M} = \tilde {H}$), no disjoining pressure effects and no evaporation, the model detailed in Appendix C simplifies to
This system was solved on the same domain and with the same simulation parameters, magnetic field, initial conditions and boundary conditions as in Moulton & Pelesko (Reference Moulton and Pelesko2010). Figure 2 presents a comparison between our simulation results and the results in figure 7 of Moulton & Pelesko (Reference Moulton and Pelesko2010). Since Moulton & Pelesko (Reference Moulton and Pelesko2010) adopt the thin film approximation in the meniscus region, where it is not valid, ![]() $x = 0$ mm and
$x = 0$ mm and ![]() $x = 45$ mm correspond to the very borders of the frame in these simulations. The agreement is almost exact when no magnetic field was applied. There is a slight deviation between the results in figure 2(b–d); however, we believe that this is because the Dirichlet boundary condition deviates from
$x = 45$ mm correspond to the very borders of the frame in these simulations. The agreement is almost exact when no magnetic field was applied. There is a slight deviation between the results in figure 2(b–d); however, we believe that this is because the Dirichlet boundary condition deviates from ![]() $h = 0.5$ mm at the top boundary (
$h = 0.5$ mm at the top boundary (![]() $x = 0$ mm) in the simulations performed by Moulton & Pelesko (Reference Moulton and Pelesko2010) when a magnetic field was applied. As a result, we consider this sufficient validation for the numerical implementation of the derived model. In § 3 the derived model is used to simulate horizontal magnetic soap films.
$x = 0$ mm) in the simulations performed by Moulton & Pelesko (Reference Moulton and Pelesko2010) when a magnetic field was applied. As a result, we consider this sufficient validation for the numerical implementation of the derived model. In § 3 the derived model is used to simulate horizontal magnetic soap films.

Figure 2. The grey line represents the initial condition. The black line and blue circles in each figure indicate the thickness after 60 s for the simulations in this study and the simulations performed in Moulton & Pelesko (Reference Moulton and Pelesko2010), respectively. The blue circles were obtained by sampling the data from figure 7 of Moulton & Pelesko (Reference Moulton and Pelesko2010) using WebPlotDigitizer (Rohatgi, Rehberg & Stanojevic Reference Rohatgi, Rehberg and Stanojevic2018). The four cases are (a) no magnetic field applied, (b) 14.5 mm between film and magnet, (c) 8.5 mm between film and magnet, and (d) 2.5 mm between film and magnet.
3. Results
In § 3.1, simulation results are used to investigate the significance of interfacial flows on the rate of film thinning, and in § 3.2, simulations results are used to study how accounting for magnetite NP transport and the dependence of the magnetisation on the magnetite NP concentration affects film thickness predictions. The simulations presented in §§ 3.1 and 3.2 were performed on a dimensionless domain defined by ![]() $\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 0.5)^2 + (\tilde {y} - 0.5)^2 \leq 0.25 \}$; the simulation parameters were chosen to investigate the phenomena of interest and are not necessarily physically realistic. In §§ 3.3 and 3.4, more realistic simulation parameters were chosen to align with the experiments in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023). The length scale
$\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 0.5)^2 + (\tilde {y} - 0.5)^2 \leq 0.25 \}$; the simulation parameters were chosen to investigate the phenomena of interest and are not necessarily physically realistic. In §§ 3.3 and 3.4, more realistic simulation parameters were chosen to align with the experiments in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023). The length scale ![]() $L$ was held fixed at the capillary length, and the simulations were conducted on a larger dimensionless domain defined by
$L$ was held fixed at the capillary length, and the simulations were conducted on a larger dimensionless domain defined by ![]() $\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 9.125)^2 + (\tilde {y} - 9.125)^2 \leq 18.25 \}$. Table 1 provides the dimensionless numbers that were used in each simulation.
$\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 9.125)^2 + (\tilde {y} - 9.125)^2 \leq 18.25 \}$. Table 1 provides the dimensionless numbers that were used in each simulation.
3.1. Effects of surface mobility and surface flows – soap films
The assumption of immobile interfaces is commonly made in thin film models for soap films and magnetic soap films. In this section we compare immobile soap films (![]() $\textit {Bq}_{\textrm{sh}} \rightarrow \infty$ and
$\textit {Bq}_{\textrm{sh}} \rightarrow \infty$ and ![]() $\textit {Bq}_{\rm d} \rightarrow \infty$, or sufficient Marangoni stresses) with partially mobile soap films to investigate the importance of including surface mobility and surface flows in thin film models, where the surface mobility can be thought of as the inverse of the Boussinesq numbers (Stone et al. Reference Stone, Koehler, Hilgenfeldt and Durand2002; Dame et al. Reference Dame, Fritz, Pitois and Faure2005), although the surface mobility also depends on Marangoni effects (Stebe, Lin & Maldarelli Reference Stebe, Lin and Maldarelli1991). Note that the fully mobile limit occurs when the interfaces are free of surface-active agents (
$\textit {Bq}_{\rm d} \rightarrow \infty$, or sufficient Marangoni stresses) with partially mobile soap films to investigate the importance of including surface mobility and surface flows in thin film models, where the surface mobility can be thought of as the inverse of the Boussinesq numbers (Stone et al. Reference Stone, Koehler, Hilgenfeldt and Durand2002; Dame et al. Reference Dame, Fritz, Pitois and Faure2005), although the surface mobility also depends on Marangoni effects (Stebe, Lin & Maldarelli Reference Stebe, Lin and Maldarelli1991). Note that the fully mobile limit occurs when the interfaces are free of surface-active agents (![]() $\textit {Bq}_{\rm sh} = \textit {Bq}_{\rm d} = 0$,
$\textit {Bq}_{\rm sh} = \textit {Bq}_{\rm d} = 0$, ![]() $\gamma = \gamma _{{\rm c}}$), which is not investigated here as surfactants are a prerequisite for films to survive for any reasonable amount of time. Gravitational effects were set to 0 (
$\gamma = \gamma _{{\rm c}}$), which is not investigated here as surfactants are a prerequisite for films to survive for any reasonable amount of time. Gravitational effects were set to 0 (![]() $\mathcal {G} = 0$) to isolate the effects of interfacial flows that arise in partially mobile films. An immobile soap film was simulated by assuming that the interface was saturated with surfactant, i.e.
$\mathcal {G} = 0$) to isolate the effects of interfacial flows that arise in partially mobile films. An immobile soap film was simulated by assuming that the interface was saturated with surfactant, i.e. ![]() $\gamma = \gamma _{\textrm{sat}}$ and
$\gamma = \gamma _{\textrm{sat}}$ and ![]() $\tilde { \gamma } = 0$, which was imposed in the simulations by setting the Marangoni number to
$\tilde { \gamma } = 0$, which was imposed in the simulations by setting the Marangoni number to ![]() $\mathcal {M} = 0$. Marangoni stresses arising due to interfacial flows driven by viscous shear from the core liquid are expected to have an immobilising effect on the interface. Consequently, the Marangoni number was varied alone for the simulated partially mobile soap films to investigate interfacial flows of varying magnitudes.
$\mathcal {M} = 0$. Marangoni stresses arising due to interfacial flows driven by viscous shear from the core liquid are expected to have an immobilising effect on the interface. Consequently, the Marangoni number was varied alone for the simulated partially mobile soap films to investigate interfacial flows of varying magnitudes.
In all simulations, the thickness field remained axisymmetric over time. Figure 3(a) presents the thickness profiles of an immobile soap film over time. The immobile film thins due to the capillary suction boundary condition with all drainage within the film governed by spatial variations in the capillary pressure. The thinning slows with time due to the ![]() $\tilde {h}^3$ dependence in the thickness evolution equation (2.42a) and the decrease in capillary suction force at the boundary with time (2.66). Furthermore, as time progresses, a region of increased film thickness forms in the centre surrounded by a thinner ring. This behaviour has been reported for circular thin films and occurs when the rate of thinning due to capillary suction exceeds the curvature-related thinning at the centre of the film (Joye, Hirasaki & Miller Reference Joye, Hirasaki and Miller1992; Pugh Reference Pugh2016).
$\tilde {h}^3$ dependence in the thickness evolution equation (2.42a) and the decrease in capillary suction force at the boundary with time (2.66). Furthermore, as time progresses, a region of increased film thickness forms in the centre surrounded by a thinner ring. This behaviour has been reported for circular thin films and occurs when the rate of thinning due to capillary suction exceeds the curvature-related thinning at the centre of the film (Joye, Hirasaki & Miller Reference Joye, Hirasaki and Miller1992; Pugh Reference Pugh2016).

Figure 3. (a) Film thickness profiles for ![]() $\tilde {t} \in [0, 1]$ along a line passing through the centre of the film at
$\tilde {t} \in [0, 1]$ along a line passing through the centre of the film at ![]() $\tilde {y} = 0.5$ for an immobile soap film and a partially mobile soap film with
$\tilde {y} = 0.5$ for an immobile soap film and a partially mobile soap film with ![]() $\mathcal {M} = 100$. The time between the thickness profiles is
$\mathcal {M} = 100$. The time between the thickness profiles is ![]() $\Delta \tilde {t} = 0.04$, and time increases in the vertically downwards direction, indicated by darker colours. (b) The average film thickness over the thin film as a function of time for an immobile film and three partially mobile films.
$\Delta \tilde {t} = 0.04$, and time increases in the vertically downwards direction, indicated by darker colours. (b) The average film thickness over the thin film as a function of time for an immobile film and three partially mobile films.
The thinning progresses considerably faster for the partially mobile soap film shown in figure 3(a) compared with the immobile film. This occurs because a surface velocity field develops that is radially outward from the centre due to viscous shear forcing from the core liquid that is also moving radially outwards from the centre. Surfactants adsorbed at the interface are advected radially outwards from the film centre, leading to Marangoni stresses that act to decelerate the surface velocity.
Faster surface flows arise with smaller Marangoni numbers, causing the average thickness over the film to fall faster with time, as shown in figure 3(b). The film thickness reaches an equilibrium when the disjoining pressure is sufficient to prevent any further drainage or evaporation. The precise equilibrium thickness obtained in this set of simulations is dependent upon the disjoining pressure parameters used in (2.63) and the strength of the capillary suction boundary condition. For the partially mobile film with ![]() $\mathcal {M} = 10$, we were able to simulate an equilibrium film by reducing the time step and slowly ramping down the Neumann slope condition from 30
$\mathcal {M} = 10$, we were able to simulate an equilibrium film by reducing the time step and slowly ramping down the Neumann slope condition from 30![]() $^\circ$ to 0
$^\circ$ to 0![]() $^\circ$ once disjoining pressure effects became significant to avoid numerical instabilities caused by large gradients in the disjoining pressure. The simulated equilibrium film thickness (
$^\circ$ once disjoining pressure effects became significant to avoid numerical instabilities caused by large gradients in the disjoining pressure. The simulated equilibrium film thickness (![]() $2h$) was 45.6 nm (
$2h$) was 45.6 nm (![]() $\tilde {h} = 2.28\times 10^{-3}$), which is a typical thickness of common black films (Bergeron Reference Bergeron1999).
$\tilde {h} = 2.28\times 10^{-3}$), which is a typical thickness of common black films (Bergeron Reference Bergeron1999).
Figure 3(b) presents how the rate of film thinning approaches the rate of thinning for the immobile soap film as the Marangoni number is increased, highlighting how Marangoni stresses can immobilise the interface. Overall, the results presented in this section highlight the importance of including interfacial flows in models for the thinning of soap films, as interfacial flows can significantly affect the rate of film thinning.
3.2. Magnetite NP transport – magnetic soap films
The drainage flows in magnetic soap films induced by an inhomogeneous magnetic field are caused by the transport of magnetic NPs within the film; this transport can affect the local magnetic NP concentration and the film magnetisation. Despite this, previous models for the thinning of magnetic soap films under the forcing of inhomogeneous magnetic fields calculate the local film magnetisation by implicitly assuming that the concentration of magnetite NPs remains uniform throughout the film (Moulton & Pelesko Reference Moulton and Pelesko2010; Back & Beckham Reference Back and Beckham2012). It is therefore of interest to understand how accounting for variations in the magnetite NP concentration and the dependence of the film magnetisation on the magnetite NP concentration affects film thickness predictions. Consequently, simulations were performed with magnetite NP transport by solving for the local molar concentration of NPs using (2.47) and without magnetite NP transport by imposing a constant and uniform concentration of magnetite NPs. The present results evaluate the possible effects and importance of accounting for magnetic NP transport when simulating magnetic soap films in inhomogeneous magnetic fields. The magnetic field used in the simulations is presented in figure 12(a).
With the capillary suction boundary condition (2.66), the thickness initially increases from right to left due to magnetically induced flows in the direction of increasing magnetic field intensity, as shown in figure 4(d). The thickness then falls to a minimum on the left side of the domain, as illustrated by figure 4(a,d), due to the magnetic drainage flux out of the thin film, which is given by ![]() $\frac {1}{3} \tilde {h}^3 \varPsi \tilde {M}(\tilde {c}, \tilde {H}) \tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$. The thickness on the left side of the domain falls faster when accounting for magnetite NP transport since the concentration of magnetite NPs, and therefore, the magnetisation, is greater on the left side of the film with magnetite NP transport compared with the case of uniform concentration. In contrast, the magnetic soap films in the experiments generally increased in thickness in the direction of increasing magnetic field intensity (Lalli et al. Reference Lalli, Shen, Dini and Giusti2023). As a result, we also investigated boundary condition (2.67), which limits the drainage flux of core liquid out of the thin film. With this boundary condition, we see a continual increase in thickness from right to left in figure 4(b,e). The difference between the thickness profiles for uniform
$\frac {1}{3} \tilde {h}^3 \varPsi \tilde {M}(\tilde {c}, \tilde {H}) \tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$. The thickness on the left side of the domain falls faster when accounting for magnetite NP transport since the concentration of magnetite NPs, and therefore, the magnetisation, is greater on the left side of the film with magnetite NP transport compared with the case of uniform concentration. In contrast, the magnetic soap films in the experiments generally increased in thickness in the direction of increasing magnetic field intensity (Lalli et al. Reference Lalli, Shen, Dini and Giusti2023). As a result, we also investigated boundary condition (2.67), which limits the drainage flux of core liquid out of the thin film. With this boundary condition, we see a continual increase in thickness from right to left in figure 4(b,e). The difference between the thickness profiles for uniform ![]() $\tilde {c}$ and with the transport of
$\tilde {c}$ and with the transport of ![]() $\tilde {c}$ is now smaller. Nevertheless, due to the build up of concentration of magnetite NPs on the left side of the film and the depletion of magnetite NPs on the right side of the film, as illustrated in figure 4(c,f), there is a larger thickness on both the left and right sides of the film when considering magnetite NP transport. This is because magnetically driven flows are stronger on the left side of the film and weaker on the right side of the film when accounting for magnetite NP transport.
$\tilde {c}$ is now smaller. Nevertheless, due to the build up of concentration of magnetite NPs on the left side of the film and the depletion of magnetite NPs on the right side of the film, as illustrated in figure 4(c,f), there is a larger thickness on both the left and right sides of the film when considering magnetite NP transport. This is because magnetically driven flows are stronger on the left side of the film and weaker on the right side of the film when accounting for magnetite NP transport.

Figure 4. The top row presents ![]() $\tilde {h}$ and
$\tilde {h}$ and ![]() $\tilde {c}$ at
$\tilde {c}$ at ![]() $\tilde {t} = 0.10$. Panels (a,b) present the thickness field with magnetite NP transport for boundary conditions (2.66) and (2.67), respectively. Panel (c) presents the concentration field for magnetite NPs for boundary condition (2.67). The profiles in (d), (e) and (f) are plots over the dashed centrelines marked in (a), (b) and (c) over time for
$\tilde {t} = 0.10$. Panels (a,b) present the thickness field with magnetite NP transport for boundary conditions (2.66) and (2.67), respectively. Panel (c) presents the concentration field for magnetite NPs for boundary condition (2.67). The profiles in (d), (e) and (f) are plots over the dashed centrelines marked in (a), (b) and (c) over time for ![]() $\tilde {t} \in [0.0, 0.2]$. The time between profiles is
$\tilde {t} \in [0.0, 0.2]$. The time between profiles is ![]() $\Delta \tilde {t} = 0.02$, and the progression of time is indicated by arrows and progressively darker colours. In (d) and (e), the dashed profiles are for a uniform concentration of magnetite NPs and the solid profiles are for magnetite NP transport governed by (2.47).
$\Delta \tilde {t} = 0.02$, and the progression of time is indicated by arrows and progressively darker colours. In (d) and (e), the dashed profiles are for a uniform concentration of magnetite NPs and the solid profiles are for magnetite NP transport governed by (2.47).
With boundary condition (2.67), the thickness profiles are more realistic; however, this boundary condition results in ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {p} _{{\rm c}} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$ varying around the boundary. Although it seems reasonable that there would be a limit on the drainage flux of core liquid out of the thin film, it is unclear, at present, whether there is any physical justification for
$\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {p} _{{\rm c}} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$ varying around the boundary. Although it seems reasonable that there would be a limit on the drainage flux of core liquid out of the thin film, it is unclear, at present, whether there is any physical justification for ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {p} _{{\rm c}} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$ varying around the boundary of the thin film, but it could possibly be attributed to the effect of the magnetic field on the meniscus shape (Rosensweig et al. Reference Rosensweig, Elborai, Lee and Zahn2005; Singh et al. Reference Singh, Singh and Bhaumik2024). Overall, accounting for the transport of magnetite NPs in thin film models can significantly affect film thickness computations since the magnetisation depends on the local NP concentration. The size of this effect is strongly dependent on the dimensionless numbers
$\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {p} _{{\rm c}} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$ varying around the boundary of the thin film, but it could possibly be attributed to the effect of the magnetic field on the meniscus shape (Rosensweig et al. Reference Rosensweig, Elborai, Lee and Zahn2005; Singh et al. Reference Singh, Singh and Bhaumik2024). Overall, accounting for the transport of magnetite NPs in thin film models can significantly affect film thickness computations since the magnetisation depends on the local NP concentration. The size of this effect is strongly dependent on the dimensionless numbers ![]() $\alpha$,
$\alpha$, ![]() $\varphi _{{\rm c}}$ and
$\varphi _{{\rm c}}$ and ![]() $Pe_{c}$, which control the strength of magnetophoresis and diffusion relative to advective transport, and the choice of the boundary condition for
$Pe_{c}$, which control the strength of magnetophoresis and diffusion relative to advective transport, and the choice of the boundary condition for ![]() $\tilde {c}$. Further research is needed to understand the behaviour of magnetite NPs at the thin film boundary,
$\tilde {c}$. Further research is needed to understand the behaviour of magnetite NPs at the thin film boundary, ![]() $\partial \varOmega$, to justify the boundary condition used for
$\partial \varOmega$, to justify the boundary condition used for ![]() $\tilde {c}$ (2.69) or to suggest an alternative boundary condition that may be more realistic.
$\tilde {c}$ (2.69) or to suggest an alternative boundary condition that may be more realistic.
3.3. Simulating experimental soap films
There are a number of unknowns from the experiments, such as the surface shear and dilatational viscosities, the initial surface excess concentration of surfactant and the initial film thickness (the films were initially too thick to exhibit interference colours (Lalli & Giusti Reference Lalli and Giusti2023)) such that it is only possible for a qualitative comparison between the simulations and the experiments.
The length scale ![]() $L$ was held fixed at the capillary length and the size of the dimensionless simulation domain was increased to
$L$ was held fixed at the capillary length and the size of the dimensionless simulation domain was increased to ![]() $\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 9.125)^2 + (\tilde {y} - 9.125)^2 \leq 18.25 \}$ to align with the experiments. With a domain of this size, capillary pressure effects are no longer significant over the entire domain, with negligible capillary pressure gradients in the centre of the domain, in contrast to the soap films simulated in § 3.1. Based on the method used to create the soap films in the experiments, we hypothesise that the pressure was slightly larger under the soap films studied. As a result, we imposed an axisymmetric centre surface,
$\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 9.125)^2 + (\tilde {y} - 9.125)^2 \leq 18.25 \}$ to align with the experiments. With a domain of this size, capillary pressure effects are no longer significant over the entire domain, with negligible capillary pressure gradients in the centre of the domain, in contrast to the soap films simulated in § 3.1. Based on the method used to create the soap films in the experiments, we hypothesise that the pressure was slightly larger under the soap films studied. As a result, we imposed an axisymmetric centre surface, ![]() $C$, of uniform curvature in the simulations, created by slicing a spherical bubble of radius 100 mm at a level such that
$C$, of uniform curvature in the simulations, created by slicing a spherical bubble of radius 100 mm at a level such that ![]() $\tilde {C}$ was 168.0 in the centre of the film and 0.0 at the thin film boundary.
$\tilde {C}$ was 168.0 in the centre of the film and 0.0 at the thin film boundary.
Figure 5 presents the dimensionless thickness field over a segment of the simulation time for two initial surface concentrations of surfactant (top row is ![]() $\tilde { \varGamma }_{\rm i} = 0.05$ and bottom row is
$\tilde { \varGamma }_{\rm i} = 0.05$ and bottom row is ![]() $\tilde { \varGamma }_{\rm i} = 0.20$). With an initially uniform thickness field, a minimum in the thickness field arises in the centre of the film for both initial concentrations of surfactant, primarily due to gravitational drainage and shear-driven surface flows. The surface flows advect surfactant outwards from the film centre, resulting in larger Marangoni stresses with increasing distance from the film centre, as illustrated in figure 6(a) for
$\tilde { \varGamma }_{\rm i} = 0.20$). With an initially uniform thickness field, a minimum in the thickness field arises in the centre of the film for both initial concentrations of surfactant, primarily due to gravitational drainage and shear-driven surface flows. The surface flows advect surfactant outwards from the film centre, resulting in larger Marangoni stresses with increasing distance from the film centre, as illustrated in figure 6(a) for ![]() $\tilde {t} = 0.01$. The film thickness and surfactant distribution is axisymmetric at this time. Furthermore, the Marangoni stresses are similar with
$\tilde {t} = 0.01$. The film thickness and surfactant distribution is axisymmetric at this time. Furthermore, the Marangoni stresses are similar with ![]() $\tilde { \varGamma }_{\rm i} = 0.05$ and
$\tilde { \varGamma }_{\rm i} = 0.05$ and ![]() $\tilde { \varGamma }_{\rm i} = 0.20$ since the Marangoni number, which features in (2.42c), is the same in each instance. After some thinning has taken place, the axisymmetry in the simulations is broken by the large Marangoni stresses at the boundary of the thin film combined with the suction boundary condition (2.66). Figure 5 presents how film that is thinner than the surrounding film is then frequently extracted from the boundary of the film before being driven towards the film centre. These thin patches of fluid initially have a higher surfactant concentration than the surrounding film, and their motion towards the film centre is driven by Marangoni stresses and the difference in gravitational forcing on thin patches of fluid compared with surrounding thicker fluid (Huang et al. Reference Huang, Iseringhausen, Kneiphof, Qu, Jiang and Hullin2020). This simulated behaviour appears to be in agreement with the mechanism for marginal regeneration outlined by Nierstrasz & Frens (Reference Nierstrasz and Frens1999).
$\tilde { \varGamma }_{\rm i} = 0.20$ since the Marangoni number, which features in (2.42c), is the same in each instance. After some thinning has taken place, the axisymmetry in the simulations is broken by the large Marangoni stresses at the boundary of the thin film combined with the suction boundary condition (2.66). Figure 5 presents how film that is thinner than the surrounding film is then frequently extracted from the boundary of the film before being driven towards the film centre. These thin patches of fluid initially have a higher surfactant concentration than the surrounding film, and their motion towards the film centre is driven by Marangoni stresses and the difference in gravitational forcing on thin patches of fluid compared with surrounding thicker fluid (Huang et al. Reference Huang, Iseringhausen, Kneiphof, Qu, Jiang and Hullin2020). This simulated behaviour appears to be in agreement with the mechanism for marginal regeneration outlined by Nierstrasz & Frens (Reference Nierstrasz and Frens1999).

Figure 5. Simulated thickness fields for ![]() $\tilde { \varGamma }_{\rm i} = 0.05$ (a) and
$\tilde { \varGamma }_{\rm i} = 0.05$ (a) and ![]() $\tilde { \varGamma }_{\rm i} = 0.20$ (b) for
$\tilde { \varGamma }_{\rm i} = 0.20$ (b) for ![]() $\tilde {t} \in [0.03, 0.165]$. The time between each thickness field is
$\tilde {t} \in [0.03, 0.165]$. The time between each thickness field is ![]() $\Delta \tilde {t} = 0.015$.
$\Delta \tilde {t} = 0.015$.

Figure 6. (a) Strength of Marangoni stresses relative to viscous shear at ![]() $\tilde {t} = 0.01$ along a line passing through the centre of the film at
$\tilde {t} = 0.01$ along a line passing through the centre of the film at ![]() $\tilde {y} = 9.125$ for
$\tilde {y} = 9.125$ for ![]() $\tilde {\varGamma }_{\rm i} = 0.05$ and
$\tilde {\varGamma }_{\rm i} = 0.05$ and ![]() $\tilde {\varGamma }_{\rm i} = 0.20$. The grey line represents the initial condition. (b) The average thickness over the entire film (solid line) and over a central circular section of film defined by
$\tilde {\varGamma }_{\rm i} = 0.20$. The grey line represents the initial condition. (b) The average thickness over the entire film (solid line) and over a central circular section of film defined by ![]() $\tilde {\varOmega }_{{\rm c}} = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 9.125)^2 + (\tilde {y} - 9.125)^2 \leq 9.125 \}$ (dashed line) as a function of time for
$\tilde {\varOmega }_{{\rm c}} = \{(\tilde {x}, \tilde {y}) \mid (\tilde {x} - 9.125)^2 + (\tilde {y} - 9.125)^2 \leq 9.125 \}$ (dashed line) as a function of time for ![]() $\tilde {\varGamma }_{\rm i} = 0.05$ and
$\tilde {\varGamma }_{\rm i} = 0.05$ and ![]() $\tilde {\varGamma }_{\rm i} = 0.20$.
$\tilde {\varGamma }_{\rm i} = 0.20$.
Figure 6(b) presents the variation of the average thickness over a central section of film and over the entire film as a function of time. There is initially a sharp change in the thickness averaged over the centre of the film for both initial surfactant concentrations. This is caused by large surface velocities arising in the initial absence of surface tension gradients, which are driven by viscous shear from the core liquid. Marangoni stresses acting to immobilise the interface arise quicker with the larger initial concentration of surfactant, ![]() $\tilde { \varGamma }_{\rm i} = 0.20$. Consequently, the film with a smaller initial concentration of surfactant drains considerably faster over time.
$\tilde { \varGamma }_{\rm i} = 0.20$. Consequently, the film with a smaller initial concentration of surfactant drains considerably faster over time.
3.4. Simulating experimental magnetic soap films
Two magnetic soap films with different concentrations of magnetite NPs (![]() $\tilde {c}_{\rm i} = 0.5$ and
$\tilde {c}_{\rm i} = 0.5$ and ![]() $\tilde {c}_{\rm i} = 1.0$) were simulated with magnetic field intensity given by figure 12(c). As
$\tilde {c}_{\rm i} = 1.0$) were simulated with magnetic field intensity given by figure 12(c). As ![]() $Pe_{c} \rightarrow \infty$ in the magnetite NP transport equation (2.47), the transport of
$Pe_{c} \rightarrow \infty$ in the magnetite NP transport equation (2.47), the transport of ![]() $\tilde {c}$ is dominated by advection. In this limit, the solution for
$\tilde {c}$ is dominated by advection. In this limit, the solution for ![]() $\tilde {c}$ is uniform for a uniform initial concentration of magnetite NPs. Preliminary simulations showed that the solution for
$\tilde {c}$ is uniform for a uniform initial concentration of magnetite NPs. Preliminary simulations showed that the solution for ![]() $\tilde {c}$ may faithfully be taken as uniform for
$\tilde {c}$ may faithfully be taken as uniform for ![]() $Pe_c = 2000$ and the other dimensionless number given in table 1. Consequently, a uniform concentration of magnetite NPs was adopted for the simulations performed in this section for computational efficiency. A centre surface of uniform curvature was imposed with smaller height than in § 3.3 to satisfy the assumption
$Pe_c = 2000$ and the other dimensionless number given in table 1. Consequently, a uniform concentration of magnetite NPs was adopted for the simulations performed in this section for computational efficiency. A centre surface of uniform curvature was imposed with smaller height than in § 3.3 to satisfy the assumption ![]() $\partial {H}/\partial {z} = 0$ over the film depth. This surface was obtained by slicing a bubble of radius 1 m such that
$\partial {H}/\partial {z} = 0$ over the film depth. This surface was obtained by slicing a bubble of radius 1 m such that ![]() $\tilde {C}$ was 16.7 in the centre of the film and 0.0 at the thin film boundary.
$\tilde {C}$ was 16.7 in the centre of the film and 0.0 at the thin film boundary.
Figure 7 presents the variation of the average thickness over the left side of the thin film, right side of the thin film and entire thin film as a function of time for the two magnetic soap films studied. Magnetically induced flows in the direction of increasing magnetic field intensity drove the average thickness to be larger on the left side of the film compared with the right side. The difference in average thickness between the left and right sides of the film is greater for the more concentrated magnetic soap film since a larger concentration of magnetite NPs leads to stronger magnetically driven flows. The average thickness over the entire thin film falls faster with ![]() $\tilde {c}_{\rm i} = 1.0$ compared with
$\tilde {c}_{\rm i} = 1.0$ compared with ![]() $\tilde {c}_{\rm i} = 0.5$, as the drainage flux out of the thin film due to magnetic forcing,
$\tilde {c}_{\rm i} = 0.5$, as the drainage flux out of the thin film due to magnetic forcing, ![]() $\frac {1}{3} \tilde {h}^3 \varPsi \tilde {M}(\tilde {c}, \tilde {H}) \tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$, is larger for
$\frac {1}{3} \tilde {h}^3 \varPsi \tilde {M}(\tilde {c}, \tilde {H}) \tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H} \boldsymbol {\cdot } \boldsymbol {n}_{\rm d}$, is larger for ![]() $\tilde {c}_{\rm i} = 1.0$.
$\tilde {c}_{\rm i} = 1.0$.

Figure 7. Average thickness over the left-half (![]() $\tilde {\varOmega }_{\mathrm {l}}$), right-half (
$\tilde {\varOmega }_{\mathrm {l}}$), right-half (![]() $\tilde {\varOmega }_{\mathrm {r}}$) and entire thin film (
$\tilde {\varOmega }_{\mathrm {r}}$) and entire thin film (![]() $\tilde {\varOmega }$) as a function of time for
$\tilde {\varOmega }$) as a function of time for ![]() $\tilde {c}_{\rm i} = 0.5$ and
$\tilde {c}_{\rm i} = 0.5$ and ![]() $\tilde {c}_{\rm i} = 1.0$.
$\tilde {c}_{\rm i} = 1.0$.
Thickness fields over a subset of the simulation time are presented in figure 8 for the two magnetic soap films studied. Figure 8 shows that film that is thinner than the surrounding fluid is sporadically extracted from the film boundary before being driven away from the film boundary. Thin patches of fluid extracted from the left side of the film move approximately in the ![]() $\boldsymbol {e}_{x}$ direction, while thin patches extracted from the right side of the film are deflected away from moving radially towards the centre of the film.
$\boldsymbol {e}_{x}$ direction, while thin patches extracted from the right side of the film are deflected away from moving radially towards the centre of the film.

Figure 8. Simulated thickness fields for ![]() $\tilde {c}_{\rm i} = 0.5$ (a) and
$\tilde {c}_{\rm i} = 0.5$ (a) and ![]() $\tilde {c}_{\rm i} = 1.0$ (b) for
$\tilde {c}_{\rm i} = 1.0$ (b) for ![]() $\tilde {t} \in [0.20, 0.38]$. The time between each thickness field is
$\tilde {t} \in [0.20, 0.38]$. The time between each thickness field is ![]() $\Delta \tilde {t} = 0.02$.
$\Delta \tilde {t} = 0.02$.
The simulated films feature fast flows in the direction of increasing magnetic field intensity that drive fast flows around the circumference of the film in the reverse direction. This behaviour is evident from the surface velocity fields in figure 9(a,c). The flows around the boundary eventually separate from the boundary and orient towards the interior of the film. The separation can be seen in figure 8 for ![]() $\tilde {t} = 0.20$, with thinner fluid being driven from the boundary at the point of separation according to the surface flows in figure 9(a,c). The point of separation occurs further to the right for the magnetic soap film with a higher concentration of magnetite NPs, as the magnetically driven surface velocities are larger for this film. In figure 9(b,d) the surface velocities are smaller due to Marangoni stresses, and the separation of the flows from the boundary occur earlier (further to the left) for each of the two magnetic soap films. Again, the separation occurs earlier for
$\tilde {t} = 0.20$, with thinner fluid being driven from the boundary at the point of separation according to the surface flows in figure 9(a,c). The point of separation occurs further to the right for the magnetic soap film with a higher concentration of magnetite NPs, as the magnetically driven surface velocities are larger for this film. In figure 9(b,d) the surface velocities are smaller due to Marangoni stresses, and the separation of the flows from the boundary occur earlier (further to the left) for each of the two magnetic soap films. Again, the separation occurs earlier for ![]() $\tilde {c}_{\rm i} = 0.5$ compared with
$\tilde {c}_{\rm i} = 0.5$ compared with ![]() $\tilde {c}_{\rm i} = 1.0$.
$\tilde {c}_{\rm i} = 1.0$.

Figure 9. A subset of surface velocity vectors for ![]() $\tilde {c}_{\rm i} = 0.5$ at (a)
$\tilde {c}_{\rm i} = 0.5$ at (a) ![]() $\tilde {t} = 0.20$ and (b)
$\tilde {t} = 0.20$ and (b) ![]() $\tilde {t} = 0.38$ and for
$\tilde {t} = 0.38$ and for ![]() $\tilde {c}_{\rm i} = 1.0$ at (c)
$\tilde {c}_{\rm i} = 1.0$ at (c) ![]() $\tilde {t} = 0.20$ and (d)
$\tilde {t} = 0.20$ and (d) ![]() $\tilde {t} = 0.38$, where
$\tilde {t} = 0.38$, where ![]() $\tilde {V}_{\rm s}$ is the magnitude of
$\tilde {V}_{\rm s}$ is the magnitude of ![]() $\tilde {\boldsymbol {V}}_{\rm s}$.
$\tilde {\boldsymbol {V}}_{\rm s}$.
4. Comparison with experiments
This section evaluates the performance of the model by comparing the results in §§ 3.3 and 3.4 with experiments. Recommendations for future work are also discussed.
4.1. Soap films
To the best of our knowledge, marginal regeneration has not been simulated before using a thin film model. The computations performed using the thin film model derived in the present study were in qualitative agreement with the drainage due to marginal regeneration observed in the experiments, namely, thin patches of fluid were extracted from the boundary of the film before moving towards the centre of the film whilst thicker fluid was sucked into the meniscus. The trajectories of the thin patches in figure 5 are in qualitative agreement with the trajectories illustrated in figure 9 of Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023).
There are some key differences between the marginal regeneration behaviour observed in the simulations (see figure 5) and in the experimentally investigated soap films (see figure 10a–c), which are now discussed. In the experiments, marginal regeneration started almost instantly after film formation, whilst the breaking of axisymmetry occurred later after around 20 s in the simulations. The mechanism that leads to pinch destabilisation and marginal regeneration, which is yet to be fully understood (Trégouët & Cantat Reference Trégouët and Cantat2021), is not incorporated into the model since the pinch lies outside of the simulated region; therefore, it may be more realistic to trigger marginal regeneration in the simulations by perturbing the film thickness or surface surfactant concentration. As evident from figures 5 and 10(a–c), the frequency of thin patches was much larger in the experiments compared with the simulations, suggesting that marginal regeneration contributed more significantly to the rate of thinning in the experiments. The thin patches were also typically larger in the simulations compared with the experiments. Since the frequency and size of thin patches is expected to be closely tied to the pinch destabilisation mechanism, a more accurate treatment of this destabilisation mechanism may lead to a better agreement between the simulations and the experiments. Furthermore, the thin patches of fluid in the experiments had well-defined, although deformable, boundaries, while the simulated thin patches had more diffusive boundaries. We hypothesise that the behaviour observed in the experiments is governed by the surfactant monolayers covering the thin patches of fluid, preventing surrounding thicker fluid from flowing into the thin patches and equilibrating their thickness with the surrounding fluid. It would be interesting to conduct further research to explore how thin patches of fluid interact with surrounding fluid, which could inform how the model could be improved to more accurately simulate marginal regeneration. The diffusive nature of the thin patches of fluid is also related to the choice of simulation parameters, such as the Péclet number for surface surfactant transport. Additionally, it may be important to account for the variation of the interfacial viscosities with the surface concentration of surfactant. Spatial gradients in the surface shear and dilatational viscosities would then enter the equation governing the surface velocity (2.42c) from the Boussinesq–Scriven surface stress model (2.15).

Figure 10. The thinning of a soap film (a–c) and magnetic soap film in an inhomogeneous magnetic field (d–f) (Lalli et al. Reference Lalli, Shen, Dini and Giusti2023), where ![]() $t$ is the time from film formation. The relationship between film thickness and interference colours was computed by applying an interference relation derived for monochromatic waves at a number of discrete wavelengths (Lalli & Giusti Reference Lalli and Giusti2023).
$t$ is the time from film formation. The relationship between film thickness and interference colours was computed by applying an interference relation derived for monochromatic waves at a number of discrete wavelengths (Lalli & Giusti Reference Lalli and Giusti2023).
A black film formed in the centre of experimentally investigated soap films, as seen in figure 10(a), within around 10 s from film formation. The black centre then grew with time, as evident from figure 10(b,c), due to drainage and evaporation. Although a minimum in thickness was observed in the centre of the simulated soap films, black film did not form. This may be attributed to the aforementioned differences in drainage due to marginal regeneration and since evaporation was switched off in all simulations.
As many surfactants are soluble, future work should focus on extending the model from insoluble surfactants to soluble surfactants. This will allow the effects of surfactant adsorption and desorption on film thinning to be explored.
4.2. Magnetic soap films
The simulated magnetic soap films shown in figure 8 feature an increase in thickness in the direction of increasing magnetic field intensity (from right to left), in alignment with the magnetic soap film shown in figure 10(d–f). Furthermore, the simulations predicted faster magnetically driven drainage flows with a larger initial concentration of magnetite NPs in the magnetic soap film, as was also reported by Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023).
The arrows in figure 10(d) illustrate the direction of the fastest drainage flows: there are flows towards the magnet in the centre of the film with reverse flows around the film boundary that then separate from the film boundary and move towards the interior of the film. Our model predictions in figures 8 and 9 predict this same flow pattern.
The trajectories of the thin patches of fluid in figure 8 are in good agreement with the trajectories in figure 9 of Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023); however, in similarity with soap films, the size and frequency of thin patches differs significantly between simulation and experiment. For example, many thin patches of fluid are present in the reverse flows around the boundary in figure 10(d–f), whilst only a few thin patches of fluid were observed in these flows in the simulated films in figure 8. As previously mentioned, a more accurate treatment of the pinch destabilisation mechanism could lead to a closer agreement between simulation and experiment. Furthermore, the frequency of thin patches of fluid depends on the proposed capillary suction boundary condition (2.66) and the suction strength, ![]() $\mathcal {P}$. This boundary condition allows the model to reproduce behaviour in qualitative agreement with marginal regeneration. Nevertheless, further research is needed to validate this boundary condition for film borders subject to capillary suction. In addition, further research is needed to justify a suitable value for the Neumann boundary condition for the film thickness, based on the behaviour in the transition region and the meniscus.
$\mathcal {P}$. This boundary condition allows the model to reproduce behaviour in qualitative agreement with marginal regeneration. Nevertheless, further research is needed to validate this boundary condition for film borders subject to capillary suction. In addition, further research is needed to justify a suitable value for the Neumann boundary condition for the film thickness, based on the behaviour in the transition region and the meniscus.
The derived model assumes a dilute concentration of magnetite NPs in the core liquid. The validity of the model could be extended to higher concentrations of magnetite NPs by considering interactions between the NPs, magnetoviscous effects and demagnetising field effects. Furthermore, the Langevin relation (2.46) describing the nonlinear magnetisation of the ferrofluid assumes that the magnetite NPs in the ferrofluid are monodisperse. Since most ferrofluids are polydisperse, it may be valuable in future work to investigate magnetisation relations derived for polydisperse NPs (Ivanov et al. Reference Ivanov, Kantorovich, Reznikov, Holm, Pshenichnikov, Lebedev, Chremos and Camp2007).
With the simulation parameters used in this study, convergence is achieved with a relatively large time step, ![]() $\Delta \tilde {t} = 0.001$ (Liu et al. Reference Liu, Peco and Dolbow2019). It is anticipated that some form of stabilisation, such as streamline-upwind Petrov–Galerkin stabilisation or a subgrid-scale method (Codina Reference Codina1998; John & Knobloch Reference John and Knobloch2007; Liu et al. Reference Liu, Peco and Dolbow2019), will be needed when forcing terms are particularly large, such as large values of
$\Delta \tilde {t} = 0.001$ (Liu et al. Reference Liu, Peco and Dolbow2019). It is anticipated that some form of stabilisation, such as streamline-upwind Petrov–Galerkin stabilisation or a subgrid-scale method (Codina Reference Codina1998; John & Knobloch Reference John and Knobloch2007; Liu et al. Reference Liu, Peco and Dolbow2019), will be needed when forcing terms are particularly large, such as large values of ![]() $\varPsi$ or
$\varPsi$ or ![]() $\mathcal {G}$, or when the Péclet numbers for magnetite NP and surfactant transport are particularly large. Finally, future work should focus on defining the range of variables and dimensionless numbers over which the pressure scale
$\mathcal {G}$, or when the Péclet numbers for magnetite NP and surfactant transport are particularly large. Finally, future work should focus on defining the range of variables and dimensionless numbers over which the pressure scale ![]() $P = {\eta U}/(\epsilon \mathcal {H})$ remains appropriate. For films close to the fully mobile limit, the pressure scale suitable for extensional flows,
$P = {\eta U}/(\epsilon \mathcal {H})$ remains appropriate. For films close to the fully mobile limit, the pressure scale suitable for extensional flows, ![]() $P = {\eta U}/{L}$, is expected to be more relevant (Kargupta et al. Reference Kargupta, Sharma and Khanna2004; Münch et al. Reference Münch, Wagner and Witelski2005), whilst for films close to rupture, inertial terms become significant such that the pressure scale
$P = {\eta U}/{L}$, is expected to be more relevant (Kargupta et al. Reference Kargupta, Sharma and Khanna2004; Münch et al. Reference Münch, Wagner and Witelski2005), whilst for films close to rupture, inertial terms become significant such that the pressure scale ![]() $P = \rho U^2$ would be more relevant (Erneux & Davis Reference Erneux and Davis1993; De Wit et al. Reference De Wit, Gallez and Christov1994).
$P = \rho U^2$ would be more relevant (Erneux & Davis Reference Erneux and Davis1993; De Wit et al. Reference De Wit, Gallez and Christov1994).
5. Concluding remarks
A system of equations governing the thickness field of free magnetic soap films has been derived using the thin film approximation. This system of equations incorporates several physical phenomena that were not accounted for in previous magnetic soap film models, such as interfacial flows and the dependence of the magnetisation on the local concentration of magnetite NPs. This model was used to simulate both soap films and magnetic soap films. It was found that interfacial flows can dominate the rate of film thinning, depending on the strength of Marangoni stresses created by the interfacial flows. Accounting for variations in the magnetite NP concentration can also have a notable effect on film thickness predictions; however, this is less important for high Péclet number (![]() $Pe_c$) flows. A capillary suction boundary condition was proposed with the aim of simulating marginal regeneration. An exchange between thin and thick fluid at the film boundary was observed in the simulations for soap films, and the simulated thin patches of fluid flowed from the film boundary towards the film centre, in agreement with the marginal regeneration phenomena observed in the experiments. The derived model was also able to reproduce several features observed in experimentally investigated magnetic soap films, such as faster magnetically driven drainage flows in the direction of increasing magnetic field intensity with larger concentrations of magnetite NPs and reverse flows that separate from the film boundary and flow into the interior of the film. This work advances the state of magnetic soap film modelling and is an important step towards more accurately modelling soap films in which marginal regeneration is occurring.
$Pe_c$) flows. A capillary suction boundary condition was proposed with the aim of simulating marginal regeneration. An exchange between thin and thick fluid at the film boundary was observed in the simulations for soap films, and the simulated thin patches of fluid flowed from the film boundary towards the film centre, in agreement with the marginal regeneration phenomena observed in the experiments. The derived model was also able to reproduce several features observed in experimentally investigated magnetic soap films, such as faster magnetically driven drainage flows in the direction of increasing magnetic field intensity with larger concentrations of magnetite NPs and reverse flows that separate from the film boundary and flow into the interior of the film. This work advances the state of magnetic soap film modelling and is an important step towards more accurately modelling soap films in which marginal regeneration is occurring.
Acknowledgements
The authors would like to thank Dr Li Shen for insightful discussions at the start of this study.
Funding
This work was supported by the Engineering and Physical Sciences Research Council (N.S.L., grant number EP/T51780X/1).
Declaration of interests
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are openly available in zenodo at https://doi.org/10.5281/zenodo.10897797.
Appendix A. Calculus on surfaces
In order to evaluate ![]() $\boldsymbol {\nabla }_{\rm s} \boldsymbol {\cdot } \boldsymbol{\mathsf{T}}_{\rm s}$, it is necessary to evaluate the surface gradient of a scalar field, the surface gradient of a vector field, the surface divergence of a vector field and the surface divergence of a second-order tensor field, where all these field are defined on the dividing surface only. This section provides the required background to perform these operations with the rectangular Cartesian coordinate system used in this study. Throughout this section, repeated Greek indices indicate a summation from 1 to 2, whilst repeated Latin indices indicate a summation from 1 to 3.
$\boldsymbol {\nabla }_{\rm s} \boldsymbol {\cdot } \boldsymbol{\mathsf{T}}_{\rm s}$, it is necessary to evaluate the surface gradient of a scalar field, the surface gradient of a vector field, the surface divergence of a vector field and the surface divergence of a second-order tensor field, where all these field are defined on the dividing surface only. This section provides the required background to perform these operations with the rectangular Cartesian coordinate system used in this study. Throughout this section, repeated Greek indices indicate a summation from 1 to 2, whilst repeated Latin indices indicate a summation from 1 to 3.
Each point on the dividing surface can be specified through two surface coordinates, which we denote by ![]() $y^{1}$ and
$y^{1}$ and ![]() $y^{2}$. The position vector of any point on the surface is then
$y^{2}$. The position vector of any point on the surface is then ![]() $\boldsymbol {r}_{\rm s} = \boldsymbol {r}_{\rm s}(y^1, y^2)$. Vector fields defined on the surface that are at every point on the surface tangential to the surface may be expressed as a linear combination of the basis
$\boldsymbol {r}_{\rm s} = \boldsymbol {r}_{\rm s}(y^1, y^2)$. Vector fields defined on the surface that are at every point on the surface tangential to the surface may be expressed as a linear combination of the basis ![]() $\{\boldsymbol {a}_{1}, \boldsymbol {a}_{2}\}$, where (Slattery et al. Reference Slattery, Sagis and Oh2007)
$\{\boldsymbol {a}_{1}, \boldsymbol {a}_{2}\}$, where (Slattery et al. Reference Slattery, Sagis and Oh2007)
The surface projection tensor, ![]() $\boldsymbol{\mathsf{P}}_{\rm s}$, is a second-order tensor field defined on the surface that maps any vector on the surface into the part of the vector tangential to the surface. The surface projection tensor may be expressed as (Slattery et al. Reference Slattery, Sagis and Oh2007)
$\boldsymbol{\mathsf{P}}_{\rm s}$, is a second-order tensor field defined on the surface that maps any vector on the surface into the part of the vector tangential to the surface. The surface projection tensor may be expressed as (Slattery et al. Reference Slattery, Sagis and Oh2007)
where ![]() ${\mathsf{a}}^{\alpha \beta }$ are the contravariant components of
${\mathsf{a}}^{\alpha \beta }$ are the contravariant components of ![]() $\boldsymbol{\mathsf{P}}_{\rm s}$. The covariant components of
$\boldsymbol{\mathsf{P}}_{\rm s}$. The covariant components of ![]() $\boldsymbol{\mathsf{P}}_{\rm s}$ are given by
$\boldsymbol{\mathsf{P}}_{\rm s}$ are given by ![]() ${\mathsf{a}}_{\alpha \beta } = \boldsymbol {a}_{\alpha } \boldsymbol {\cdot } \boldsymbol {a}_{\beta }$, and the contravariant components can be found from the covariant components through (Slattery et al. Reference Slattery, Sagis and Oh2007)
${\mathsf{a}}_{\alpha \beta } = \boldsymbol {a}_{\alpha } \boldsymbol {\cdot } \boldsymbol {a}_{\beta }$, and the contravariant components can be found from the covariant components through (Slattery et al. Reference Slattery, Sagis and Oh2007)
where ![]() $\textrm {e}^{\alpha \beta }$ is the Levi-Civita symbol in two dimensions and
$\textrm {e}^{\alpha \beta }$ is the Levi-Civita symbol in two dimensions and ![]() $a$ is the determinant of the square matrix with entries
$a$ is the determinant of the square matrix with entries ![]() ${\mathsf{a}}_{\alpha \beta }$.
${\mathsf{a}}_{\alpha \beta }$.
For a scalar field ![]() $A$, vector field
$A$, vector field ![]() $\boldsymbol {A}$ and second-order tensor field
$\boldsymbol {A}$ and second-order tensor field ![]() $\boldsymbol{\mathsf{A}}$, all defined on the dividing surface, the required surface operations for evaluating
$\boldsymbol{\mathsf{A}}$, all defined on the dividing surface, the required surface operations for evaluating ![]() $\boldsymbol {\nabla }_{\rm s} \boldsymbol {\cdot } \boldsymbol{\mathsf{T}}_{\rm s}$ are defined by (Slattery et al. Reference Slattery, Sagis and Oh2007)
$\boldsymbol {\nabla }_{\rm s} \boldsymbol {\cdot } \boldsymbol{\mathsf{T}}_{\rm s}$ are defined by (Slattery et al. Reference Slattery, Sagis and Oh2007)
We now introduce the rectangular Cartesian coordinate system, with basis ![]() $\{\boldsymbol {e}_{x},\boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$ and coordinates
$\{\boldsymbol {e}_{x},\boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$ and coordinates ![]() $\{x, y, z\}$, used in this study. Since the dividing surface was defined at
$\{x, y, z\}$, used in this study. Since the dividing surface was defined at ![]() $z = h(x,y,t)$,
$z = h(x,y,t)$, ![]() $x$ and
$x$ and ![]() $y$ were used as the surface coordinates such that
$y$ were used as the surface coordinates such that ![]() $\boldsymbol {r}_{\rm s} = x \boldsymbol {e}_{x} + y \boldsymbol {e}_{y} + h(x, y, t) \boldsymbol {e}_{z}$. We may then use (A1) and (A3) to find
$\boldsymbol {r}_{\rm s} = x \boldsymbol {e}_{x} + y \boldsymbol {e}_{y} + h(x, y, t) \boldsymbol {e}_{z}$. We may then use (A1) and (A3) to find
 $$\begin{gather}{\mathsf{a}}^{11} = \frac{1}{a} \left(1 + \left( \frac{\partial{h}}{\partial{y}}\right)^2 \right) , \end{gather}$$
$$\begin{gather}{\mathsf{a}}^{11} = \frac{1}{a} \left(1 + \left( \frac{\partial{h}}{\partial{y}}\right)^2 \right) , \end{gather}$$ $$\begin{gather} {\mathsf{a}}^{22} = \frac{1}{a} \left(1 + \left( \frac{\partial{h}}{\partial{x}} \right)^2 \right) . \end{gather}$$
$$\begin{gather} {\mathsf{a}}^{22} = \frac{1}{a} \left(1 + \left( \frac{\partial{h}}{\partial{x}} \right)^2 \right) . \end{gather}$$
With the centre surface included, ![]() $h$ must be replaced by
$h$ must be replaced by ![]() $h+C$ in (A5). In order to evaluate the surface operations defined in (A4), all that remains is to express
$h+C$ in (A5). In order to evaluate the surface operations defined in (A4), all that remains is to express ![]() $\boldsymbol {A}$ and
$\boldsymbol {A}$ and ![]() $\boldsymbol{\mathsf{A}}$ in terms of their rectangular Cartesian components. For brevity, we use
$\boldsymbol{\mathsf{A}}$ in terms of their rectangular Cartesian components. For brevity, we use ![]() $\{\boldsymbol {e}_1, \boldsymbol {e}_2, \boldsymbol {e}_3\}$ to denote
$\{\boldsymbol {e}_1, \boldsymbol {e}_2, \boldsymbol {e}_3\}$ to denote ![]() $\{\boldsymbol {e}_{x}, \boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$. With
$\{\boldsymbol {e}_{x}, \boldsymbol {e}_{y}, \boldsymbol {e}_{z}\}$. With ![]() $\boldsymbol {A} = A_i \boldsymbol {e}_i$, (A4b) and (A4c) become
$\boldsymbol {A} = A_i \boldsymbol {e}_i$, (A4b) and (A4c) become
Similarly, with ![]() $\boldsymbol{\mathsf{A}} = {\mathsf{A}}_{ij} \boldsymbol {e}_i \boldsymbol {e}_{j}$, (A4d) becomes
$\boldsymbol{\mathsf{A}} = {\mathsf{A}}_{ij} \boldsymbol {e}_i \boldsymbol {e}_{j}$, (A4d) becomes
The presented results allow the surface operations featuring in the present study to be evaluated, for example, the surface gradient of the surface tension and the surface divergence of the surface velocity field are
 \begin{align}
\boldsymbol{\nabla}_{\rm
s}\gamma & = \boldsymbol{e}_{x} \left({\mathsf{a}}^{11} \frac{\partial \gamma}{\partial x} +
{\mathsf{a}}^{21}\frac{\partial \gamma}{\partial y} \right) + \boldsymbol{e}_{y}
\left({\mathsf{a}}^{12} \frac{\partial \gamma}{\partial x} + {\mathsf{a}}^{22} \frac{\partial \gamma}{\partial y} \right)
\nonumber\\ & \quad + \boldsymbol{e}_{z} \left({\mathsf{a}}^{11} \frac{\partial \gamma}{\partial x} \frac{\partial{h}}{\partial{x}} + {\mathsf{a}}^{12} \frac{\partial \gamma}{\partial x} \frac{\partial{h}}{\partial{y}} + {\mathsf{a}}^{21} \frac{\partial \gamma}{\partial y} \frac{\partial{h}}{\partial{x}} + {\mathsf{a}}^{22} \frac{\partial \gamma}{\partial y} \frac{\partial{h}}{\partial{y}}\right) ,
\end{align}
\begin{align}
\boldsymbol{\nabla}_{\rm
s}\gamma & = \boldsymbol{e}_{x} \left({\mathsf{a}}^{11} \frac{\partial \gamma}{\partial x} +
{\mathsf{a}}^{21}\frac{\partial \gamma}{\partial y} \right) + \boldsymbol{e}_{y}
\left({\mathsf{a}}^{12} \frac{\partial \gamma}{\partial x} + {\mathsf{a}}^{22} \frac{\partial \gamma}{\partial y} \right)
\nonumber\\ & \quad + \boldsymbol{e}_{z} \left({\mathsf{a}}^{11} \frac{\partial \gamma}{\partial x} \frac{\partial{h}}{\partial{x}} + {\mathsf{a}}^{12} \frac{\partial \gamma}{\partial x} \frac{\partial{h}}{\partial{y}} + {\mathsf{a}}^{21} \frac{\partial \gamma}{\partial y} \frac{\partial{h}}{\partial{x}} + {\mathsf{a}}^{22} \frac{\partial \gamma}{\partial y} \frac{\partial{h}}{\partial{y}}\right) ,
\end{align}
 \begin{align} \boldsymbol{\nabla}_{\rm
s} \boldsymbol{\cdot} \boldsymbol{V}_{\rm s} & = {\mathsf{a}}^{11}
\left(\frac{\partial u_{\mathrm{s}}}{\partial x} +
\frac{\partial h}{\partial x}\frac{\partial
w_{\mathrm{s}}}{\partial x}\right) + {\mathsf{a}}^{22} \left(
\frac{\partial v_{\mathrm{s}}}{\partial y} + \frac{\partial
h}{\partial y}\frac{\partial w_{\mathrm{s}}}{\partial y}
\right) \nonumber\\ & \quad + {\mathsf{a}}^{12} \left( \frac{\partial
u_{\rm s}}{\partial y} + \frac{\partial h}{\partial
x}\frac{\partial w_{\mathrm{s}}}{\partial y} +
\frac{\partial v_{\mathrm{s}}}{\partial x} + \frac{\partial
h}{\partial y}\frac{\partial w_{\mathrm{s}}}{\partial x}
\right) . \end{align}
\begin{align} \boldsymbol{\nabla}_{\rm
s} \boldsymbol{\cdot} \boldsymbol{V}_{\rm s} & = {\mathsf{a}}^{11}
\left(\frac{\partial u_{\mathrm{s}}}{\partial x} +
\frac{\partial h}{\partial x}\frac{\partial
w_{\mathrm{s}}}{\partial x}\right) + {\mathsf{a}}^{22} \left(
\frac{\partial v_{\mathrm{s}}}{\partial y} + \frac{\partial
h}{\partial y}\frac{\partial w_{\mathrm{s}}}{\partial y}
\right) \nonumber\\ & \quad + {\mathsf{a}}^{12} \left( \frac{\partial
u_{\rm s}}{\partial y} + \frac{\partial h}{\partial
x}\frac{\partial w_{\mathrm{s}}}{\partial y} +
\frac{\partial v_{\mathrm{s}}}{\partial x} + \frac{\partial
h}{\partial y}\frac{\partial w_{\mathrm{s}}}{\partial x}
\right) . \end{align}
Appendix B. Material properties and scales
Table 2 provides typical properties and scales for soap films created from aqueous-surfactant solutions and magnetic soap films created from aqueous-surfactant solutions containing a dilute concentration of magnetite NPs.
Table 2. Typical properties and scales for soap films and magnetic soap films created from aqueous-surfactant solutions and with magnetite NPs providing the source of magnetism in the magnetic soap films. The data in Rosen & Kunjappu (Reference Rosen and Kunjappu2012), Bergfreund et al. (Reference Bergfreund, Siegenthaler, Lutz-Bueno, Bertsch and Fischer2021) was used for the surface tension and surface excess concentration of surfactant for a saturated interface, ![]() $\gamma _{\textrm{sat}}$ and
$\gamma _{\textrm{sat}}$ and ![]() $\varGamma _{\textrm{sat}}$. The values for the surface shear viscosity,
$\varGamma _{\textrm{sat}}$. The values for the surface shear viscosity, ![]() $\eta _{\rm s}$, were taken from Dimova et al. (Reference Dimova, Danov, Pouligny and Ivanov2000), Stevenson (Reference Stevenson2005), and the values for the surface dilatational viscosity,
$\eta _{\rm s}$, were taken from Dimova et al. (Reference Dimova, Danov, Pouligny and Ivanov2000), Stevenson (Reference Stevenson2005), and the values for the surface dilatational viscosity, ![]() $\lambda _{\rm s}$, were taken from Fruhner et al. (Reference Fruhner, Wantke and Lunkenheimer2000), Wantke, Fruhner & Örtegren (Reference Wantke, Fruhner and Örtegren2003). The disjoining pressure coefficients in (2.63) were estimated using data in Lyklema & Mysels (Reference Lyklema and Mysels1965), Casteletto et al. (Reference Casteletto, Cantat, Sarker, Bausch, Bonn and Meunier2003), Matsubara et al. (Reference Matsubara, Kimura, Miyao, Shin and Ikeda2021). The magnetic dipole moment,
$\lambda _{\rm s}$, were taken from Fruhner et al. (Reference Fruhner, Wantke and Lunkenheimer2000), Wantke, Fruhner & Örtegren (Reference Wantke, Fruhner and Örtegren2003). The disjoining pressure coefficients in (2.63) were estimated using data in Lyklema & Mysels (Reference Lyklema and Mysels1965), Casteletto et al. (Reference Casteletto, Cantat, Sarker, Bausch, Bonn and Meunier2003), Matsubara et al. (Reference Matsubara, Kimura, Miyao, Shin and Ikeda2021). The magnetic dipole moment, ![]() $m$, was calculated using a magnetic core diameter of 10 nm with the ferrofluid properties in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023), and the particle volume including the coating,
$m$, was calculated using a magnetic core diameter of 10 nm with the ferrofluid properties in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023), and the particle volume including the coating, ![]() $\mathcal {V}_{\rm p}$, was calculated by assuming a coating thickness of 2 nm (Ivanov et al. Reference Ivanov, Kantorovich, Reznikov, Holm, Pshenichnikov, Lebedev, Chremos and Camp2007). The Brownian diffusion coefficient of the magnetite NPs,
$\mathcal {V}_{\rm p}$, was calculated by assuming a coating thickness of 2 nm (Ivanov et al. Reference Ivanov, Kantorovich, Reznikov, Holm, Pshenichnikov, Lebedev, Chremos and Camp2007). The Brownian diffusion coefficient of the magnetite NPs, ![]() $D_0$, was computed by using the hydrodynamic radius of the NPs in the ferrofluid (56 nm) in place of
$D_0$, was computed by using the hydrodynamic radius of the NPs in the ferrofluid (56 nm) in place of ![]() $a$ in (2.45). Finally, the values in Dimova et al. (Reference Dimova, Danov, Pouligny and Ivanov2000), Craster & Matar (Reference Craster and Matar2009) were used for the surface diffusion coefficient,
$a$ in (2.45). Finally, the values in Dimova et al. (Reference Dimova, Danov, Pouligny and Ivanov2000), Craster & Matar (Reference Craster and Matar2009) were used for the surface diffusion coefficient, ![]() $D_{\rm s}$.
$D_{\rm s}$.

Appendix C. Free vertical magnetic soap films
The simplest way to adapt the derived model to free vertical magnetic soap films is to keep the dividing surface at ![]() $z = h$ (a centre surface is not considered for vertical films). We, therefore, rotate the coordinate system so that
$z = h$ (a centre surface is not considered for vertical films). We, therefore, rotate the coordinate system so that ![]() $\boldsymbol {e}_{x}$ is in the vertically downwards direction and
$\boldsymbol {e}_{x}$ is in the vertically downwards direction and ![]() $\boldsymbol {e}_{y}$ is across the film, as shown in figure 11(a). Gravitational forcing now enters through the
$\boldsymbol {e}_{y}$ is across the film, as shown in figure 11(a). Gravitational forcing now enters through the ![]() $x$-momentum equation, and the resulting system of equations is
$x$-momentum equation, and the resulting system of equations is
with the magnetite NP and surfactant transport equations still given by (2.47) and (2.61). The assumptions that were used in the derivation of (2.42a–c), such as ![]() $\partial H/\partial z = 0$ over the thickness of the film, also apply to these equations governing the thickness evolution of free vertical magnetic soap films (C1a–c).
$\partial H/\partial z = 0$ over the thickness of the film, also apply to these equations governing the thickness evolution of free vertical magnetic soap films (C1a–c).

Figure 11. (a) A schematic of a free vertical soap film bounded by a frame, in the ![]() $x$–
$x$–![]() $y$ plane, (b) presents a zoomed-in cross-section of a small section of the thin film in (a) in the
$y$ plane, (b) presents a zoomed-in cross-section of a small section of the thin film in (a) in the ![]() $x$–
$x$–![]() $z$ plane, and (c) shows the simulated thickness field of a free vertical soap film on dimensionless domain
$z$ plane, and (c) shows the simulated thickness field of a free vertical soap film on dimensionless domain ![]() $\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid 0 \leq \tilde {x} \leq 20; 0 \leq \tilde {y} \leq 20\}$ for
$\tilde { \varOmega } = \{(\tilde {x}, \tilde {y}) \mid 0 \leq \tilde {x} \leq 20; 0 \leq \tilde {y} \leq 20\}$ for ![]() $\tilde {t} \in [0.1, 2.0]$.
$\tilde {t} \in [0.1, 2.0]$.
Figure 11(c) presents an example simulation of a free vertical soap film bounded by a square frame. All simulation parameters, boundary conditions and initial conditions were the same as for § 3.3 in table 1, except ![]() $\mathcal {G} = 1$,
$\mathcal {G} = 1$, ![]() $\mathcal {M} = 500$,
$\mathcal {M} = 500$, ![]() $\textit {Bq}_{\textrm{sh}} = \textit {Bq}_{\rm d} = 5\times 10^{-4}$,
$\textit {Bq}_{\textrm{sh}} = \textit {Bq}_{\rm d} = 5\times 10^{-4}$, ![]() $\tilde { \varGamma }_{\rm i} = 0.1$ and
$\tilde { \varGamma }_{\rm i} = 0.1$ and ![]() $N_{\textrm{cell}} = 258\,000$ were used for the simulated vertical soap film. The film thickness increases in the positive
$N_{\textrm{cell}} = 258\,000$ were used for the simulated vertical soap film. The film thickness increases in the positive ![]() $\boldsymbol {e}_{x}$ direction, predominately due to gravitational drainage. Furthermore, thin patches of fluid are extracted from the bottom film boundary and rise upwards due to Marangoni stresses (Nierstrasz & Frens Reference Nierstrasz and Frens1999) and gravitational effects (Huang et al. Reference Huang, Iseringhausen, Kneiphof, Qu, Jiang and Hullin2020). This behaviour is in qualitative agreement with the marginal regeneration phenomena observed in experimental images of free vertical soap films in Nierstrasz & Frens (Reference Nierstrasz and Frens1999) and Berg et al. (Reference Berg, Adelizzi and Troian2005); however, the frequency and size of thin patches of fluid differ between this simulation and these images.
$\boldsymbol {e}_{x}$ direction, predominately due to gravitational drainage. Furthermore, thin patches of fluid are extracted from the bottom film boundary and rise upwards due to Marangoni stresses (Nierstrasz & Frens Reference Nierstrasz and Frens1999) and gravitational effects (Huang et al. Reference Huang, Iseringhausen, Kneiphof, Qu, Jiang and Hullin2020). This behaviour is in qualitative agreement with the marginal regeneration phenomena observed in experimental images of free vertical soap films in Nierstrasz & Frens (Reference Nierstrasz and Frens1999) and Berg et al. (Reference Berg, Adelizzi and Troian2005); however, the frequency and size of thin patches of fluid differ between this simulation and these images.
Appendix D. Applied magnetic field
Figure 12 presents the applied magnetic fields over the spatial region of the thin film, ![]() $\varOmega$, that were used in the simulations. The characteristic magnetic field intensity,
$\varOmega$, that were used in the simulations. The characteristic magnetic field intensity, ![]() $H_{{\rm c}}$, was chosen as the maximum value of the magnetic field intensity,
$H_{{\rm c}}$, was chosen as the maximum value of the magnetic field intensity, ![]() $H$, in
$H$, in ![]() $\varOmega$. The applied magnetic field used in simulations performed in § 3.2 is shown in the top row of figure 12, whilst the applied magnetic field used in simulations performed in § 3.4 is shown in the bottom row of figure 12. These magnetic fields were calculated using Magpylib (Ortner & Bandeira Reference Ortner and Bandeira2020) by assuming a cylindrical magnet of homogeneous magnetisation with remanence equal to 1430 mT. This approach was justified in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) by comparison with measurements made using an F71 Teslameter. Both
$\varOmega$. The applied magnetic field used in simulations performed in § 3.2 is shown in the top row of figure 12, whilst the applied magnetic field used in simulations performed in § 3.4 is shown in the bottom row of figure 12. These magnetic fields were calculated using Magpylib (Ortner & Bandeira Reference Ortner and Bandeira2020) by assuming a cylindrical magnet of homogeneous magnetisation with remanence equal to 1430 mT. This approach was justified in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023) by comparison with measurements made using an F71 Teslameter. Both ![]() $\tilde {H}$ and
$\tilde {H}$ and ![]() $|\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}|$ increase from right to left, as the neodymium magnet was placed on the left side of the film.
$|\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}|$ increase from right to left, as the neodymium magnet was placed on the left side of the film.

Figure 12. The top row shows (a) the applied magnetic field, ![]() $\tilde {H}$, and (b) the gradient
$\tilde {H}$, and (b) the gradient ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}$ over the thin film region,
$\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}$ over the thin film region, ![]() $\varOmega$, for a cylindrical magnet with diameter 10 mm, thickness 10 mm and
$\varOmega$, for a cylindrical magnet with diameter 10 mm, thickness 10 mm and ![]() $H_{{\rm c}} = 180.4$ kA m
$H_{{\rm c}} = 180.4$ kA m![]() $^{-1}$. The bottom row shows the same for a cylindrical magnet with the same dimensions and properties as the neodymium magnet used in the experiments: diameter 38.5 mm, thickness 10 mm and
$^{-1}$. The bottom row shows the same for a cylindrical magnet with the same dimensions and properties as the neodymium magnet used in the experiments: diameter 38.5 mm, thickness 10 mm and ![]() $H_{{\rm c}} = 218.9$ kA m
$H_{{\rm c}} = 218.9$ kA m![]() $^{-1}$. The arrows in (b) and (d) represent the direction of
$^{-1}$. The arrows in (b) and (d) represent the direction of ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}$, and the colours represent the magnitude of
$\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}$, and the colours represent the magnitude of ![]() $\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}$.
$\tilde {\boldsymbol {\nabla }}_{\rm p} \tilde {H}$.