Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2025-01-05T19:23:04.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermo-osmotic flow in slit channels with boundary slip: giant flow amplification between polarized graphene surfaces

Published online by Cambridge University Press:  24 July 2023

Doyel Pandey Open the ORCID record for Doyel Pandey [Opens in a new window]  and
Steffen Hardt Open the ORCID record for Steffen Hardt [Opens in a new window]
Doyel Pandey
Affiliation:
Fachbereich Maschinenbau, Fachgebiet Nano- und Mikrofluidik, Technische Universität Darmstadt, Peter-Grünberg-Straße 10, 64287 Darmstadt, Germany
Steffen Hardt*
Affiliation:
Fachbereich Maschinenbau, Fachgebiet Nano- und Mikrofluidik, Technische Universität Darmstadt, Peter-Grünberg-Straße 10, 64287 Darmstadt, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

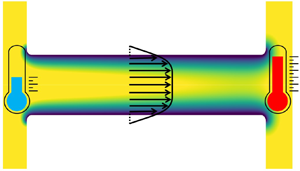
The thermo-osmotic flow (TOF) of an electrolyte solution in a slit channel with a Navier slip condition at the channel walls is studied. An analytical expression for the TOF velocity profile, based on the long-wavelength and Debye–Hückel approximations, is derived and compared to numerical solutions based on the finite-element method. The TOF between graphene surfaces whose charge is created via polarization through an applied electric field is considered as a special case. Using the relationship between the surface charge and the slip length obtained from molecular dynamics simulations, a giant flow amplification is uncovered. Specifically, for such flow in a channel with a width of 10 nm, compared to the flow between no-slip walls, a flow velocity enhancement by a factor of up to 250 is predicted.

JFM classification

Low-Reynolds-number flows: Lubrication theory MHD and Electrohydrodynamics: Electrokinetic flows Micro-/Nano-fluid dynamics: Microscale transport
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 967 , 25 July 2023 , R5
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajdari, A. & Bocquet, L. 2006 Giant amplification of interfacially driven transport by hydrodynamic slip: diffusio-osmosis and beyond. Phys. Rev. Lett. 96 (18), 186102.CrossRefGoogle ScholarPubMed
Akhlaghi, H., Roohi, E. & Stefanov, S. 2023 A comprehensive review on micro-and nano-scale gas flow effects: slip-jump phenomena, Knudsen paradox, thermally-driven flows, and Knudsen pumps. Phys. Rep. 997, 1–60.CrossRefGoogle Scholar
Balme, S., Picaud, F., Manghi, M., Palmeri, J., Bechelany, M., Cabello-Aguilar, S., Abou-Chaaya, A., Miele, P., Balanzat, E. & Janot, J.M. 2015 Ionic transport through sub-10 nm diameter hydrophobic high-aspect ratio nanopores: experiment, theory and simulation. Sci. Rep. 5 (1), 10135.CrossRefGoogle ScholarPubMed
Botan, A., Marry, V., Rotenberg, B., Turq, P. & Noetinger, B. 2013 How electrostatics influences hydrodynamic boundary conditions: Poiseuille and electro-osmostic flows in clay nanopores. J. Phys. Chem. C 117 (2), 978–985.CrossRefGoogle Scholar
Chen, K., Yao, L. & Su, B. 2019 Bionic thermoelectric response with nanochannels. J. Am. Chem. Soc. 141 (21), 8608–8615.CrossRefGoogle ScholarPubMed
Dietzel, M. & Hardt, S. 2017 Flow and streaming potential of an electrolyte in a channel with an axial temperature gradient. J. Fluid Mech. 813, 1060–1111.CrossRefGoogle Scholar
Fu, L., Joly, L. & Merabia, S. 2019 Giant thermoelectric response of nanofluidic systems driven by water excess enthalpy. Phys. Rev. Lett. 123 (13), 138001.CrossRefGoogle ScholarPubMed
Fu, L., Merabia, S. & Joly, L. 2017 What controls thermo-osmosis? Molecular simulations show the critical role of interfacial hydrodynamics. Phys. Rev. Lett. 119 (21), 214501.CrossRefGoogle ScholarPubMed
Geng, X., Yu, M., Zhang, W., Liu, Q., Yu, X. & Lu, Y. 2019 Slip length and structure of liquid water flowing past atomistic smooth charged walls. Sci. Rep. 9 (1), 18957.CrossRefGoogle ScholarPubMed
He, Y., Tsutsui, M., Miao, X.S. & Taniguchi, M. 2015 Impact of water-depletion layer on transport in hydrophobic nanochannels. Anal. Chem. 87 (24), 12040–12050.CrossRefGoogle ScholarPubMed
Herrero, C., De San Féliciano, M., Merabia, S. & Joly, L. 2022 Fast and versatile thermo-osmotic flows with a pinch of salt. Nanoscale 14 (3), 626–631.CrossRefGoogle ScholarPubMed
Huang, D.M., Cottin-Bizonne, C., Ybert, C. & Bocquet, L. 2008 Aqueous electrolytes near hydrophobic surfaces: dynamic effects of ion specificity and hydrodynamic slip. Langmuir 24 (4), 1442–1450.CrossRefGoogle ScholarPubMed
Israelachvili, J.N. 2011 Intermolecular and Surface Forces. Academic Press.Google Scholar
Jing, D. & Bhushan, B. 2013 Quantification of surface charge density and its effect on boundary slip. Langmuir 29 (23), 6953–6963.CrossRefGoogle ScholarPubMed
Joly, L., Ybert, C., Trizac, E. & Bocquet, L. 2004 Hydrodynamics within the electric double layer on slipping surfaces. Phys. Rev. Lett. 93 (25), 257805.CrossRefGoogle ScholarPubMed
Joly, L., Ybert, C., Trizac, E. & Bocquet, L. 2006 Liquid friction on charged surfaces: from hydrodynamic slippage to electrokinetics. J. Chem. Phys. 125 (20), 204716.CrossRefGoogle ScholarPubMed
Li, Y. & Bhushan, B. 2015 The effect of surface charge on the boundary slip of various oleophilic/phobic surfaces immersed in liquids. Soft Matt. 11 (38), 7680–7695.CrossRefGoogle ScholarPubMed
Maheedhara, R.S., Jing, H., Sachar, H.S. & Das, S. 2018 Highly enhanced liquid flows via thermoosmotic effects in soft and charged nanochannels. Phys. Chem. Chem. Phys. 20 (37), 24300–24316.CrossRefGoogle ScholarPubMed
Marbach, S. & Bocquet, L. 2019 Osmosis, from molecular insights to large-scale applications. Chem. Soc. Rev. 48 (11), 3102–3144.CrossRefGoogle ScholarPubMed
Masliyah, J.H. & Bhattacharjee, S. 2006 Electrokinetic and Colloid Transport Phenomena. John Wiley & Sons.CrossRefGoogle Scholar
Pan, Y. & Bhushan, B. 2013 Role of surface charge on boundary slip in fluid flow. J. Colloid Interface Sci. 392, 117–121.CrossRefGoogle ScholarPubMed
Russel, W.B., Russel, W.B., Saville, D.A. & Schowalter, W.R. 1991 Colloidal Dispersions. Cambridge University Press.Google Scholar
Sivasankar, V.S., Etha, S.A., Sachar, H.S. & Das, S. 2021 Thermo-osmotic transport in nanochannels grafted with ph-responsive polyelectrolyte brushes modelled using augmented strong stretching theory. J. Fluid Mech. 917, A31.CrossRefGoogle Scholar
Wang, X., Su, T., Zhang, W., Zhang, Z. & Zhang, S. 2020 Knudsen pumps: a review. Microsyst. Nanoengng 6 (1), 26.CrossRefGoogle ScholarPubMed
Würger, A. 2010 Thermal non-equilibrium transport in colloids. Rep. Prog. Phys. 73 (12), 126601.CrossRefGoogle Scholar
Xie, Y., Fu, L., Niehaus, T. & Joly, L. 2020 Liquid-solid slip on charged walls: the dramatic impact of charge distribution. Phys. Rev. Lett. 125 (1), 014501.CrossRefGoogle ScholarPubMed
Zhang, W., Farhan, M., Jiao, K., Qian, F., Guo, P., Wang, Q., Yang, C.C. & Zhao, C. 2022 Simultaneous thermoosmotic and thermoelectric responses in nanoconfined electrolyte solutions: effects of nanopore structures and membrane properties. J. Colloid Interface Sci. 618, 333–351.CrossRefGoogle ScholarPubMed
Zhang, W., Wang, Q., Zeng, M. & Zhao, C. 2019 Thermoelectric effect and temperature-gradient-driven electrokinetic flow of electrolyte solutions in charged nanocapillaries. Intl J. Heat Mass Transfer 143, 118569.CrossRefGoogle Scholar