Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Petkovšek, Martin
and
Dular, Matevž
2013.
IR measurements of the thermodynamic effects in cavitating flow.
International Journal of Heat and Fluid Flow,
Vol. 44,
Issue. ,
p.
756.
Quinto-Su, Pedro A.
Suzuki, Madoka
and
Ohl, Claus-Dieter
2014.
Fast temperature measurement following single laser-induced cavitation inside a microfluidic gap.
Scientific Reports,
Vol. 4,
Issue. 1,
Petkovšek, M
and
Dular, M
2015.
Experimental study of the thermodynamic effect in a cavitating flow on a simple Venturi geometry.
Journal of Physics: Conference Series,
Vol. 656,
Issue. ,
p.
012179.
Petkovšek, Martin
Mlakar, Matej
Levstek, Marjetka
Stražar, Marjeta
Širok, Brane
and
Dular, Matevž
2015.
A novel rotation generator of hydrodynamic cavitation for waste-activated sludge disintegration.
Ultrasonics Sonochemistry,
Vol. 26,
Issue. ,
p.
408.
Duke, Daniel
Swantek, Andrew
Kastengren, Alan
Fezzaa, Kamel
and
Powell, Christopher
2015.
Recent Developments in X-ray Diagnostics for Cavitation.
SAE International Journal of Fuels and Lubricants,
Vol. 8,
Issue. 1,
p.
135.
Dular, Matevž
2016.
Hydrodynamic cavitation damage in water at elevated temperatures.
Wear,
Vol. 346-347,
Issue. ,
p.
78.
Chen, Tairan
Huang, Biao
Wang, Guoyu
and
Zhao, Xing’an
2016.
Numerical study of cavitating flows in a wide range of water temperatures with special emphasis on two typical cavitation dynamics.
International Journal of Heat and Mass Transfer,
Vol. 101,
Issue. ,
p.
886.
Petkovšek, Martin
and
Dular, Matevž
2017.
Observing the thermodynamic effects in cavitating flow by IR thermography.
Experimental Thermal and Fluid Science,
Vol. 88,
Issue. ,
p.
450.
Long, Xin-ping
Wang, Qing-qing
Xiao, Long-zhou
Zhang, Jun-qiang
Xu, Mao-sen
Wu, Wei-feng
and
Ji, Bin
2017.
Numerical analysis of bubble dynamics in the diffuser of a jet pump under variable ambient pressure.
Journal of Hydrodynamics,
Vol. 29,
Issue. 3,
p.
510.
Daou, Maya Mounir
Igualada, Elena
Dutilleul, Hugo
Citerne, Jean‐Marie
Rodríguez‐Rodríguez, Javier
Zaleski, Stéphane
and
Fuster, Daniel
2017.
Investigation of the collapse of bubbles after the impact of a piston on a liquid free surface.
AIChE Journal,
Vol. 63,
Issue. 6,
p.
2483.
Wang, Jingzhu
Abe, Akihisa
Koita, Taketoshi
Sun, Mingyu
Wang, Yiwei
and
Huang, Chenguang
2018.
Study of sterilization effects on marine Vibrio sp. using interaction of cavitation with shock wave in a narrow water chamber.
Journal of Applied Physics,
Vol. 124,
Issue. 21,
Syamsundar, C.
Chatterjee, Dhiman
and
Kamaraj, M.
2018.
Improved Resistance of Nanoparticle-Laden Polymer Coatings Subjected to Combined Silt and Cavitation.
Materials Performance and Characterization,
Vol. 7,
Issue. 5,
p.
1127.
Dular, Matevž
and
Petkovšek, Martin
2018.
Cavitation erosion in liquid nitrogen.
Wear,
Vol. 400-401,
Issue. ,
p.
111.
Wang, Jingzhu
Abe, Akihisa
Wang, Yiwei
and
Huang, Chenguang
2018.
Fundamental study of sterilization effects on marine Vibrio sp. in a cylindrical water chamber with supply of only underwater shock waves.
Ultrasonics Sonochemistry,
Vol. 42,
Issue. ,
p.
541.
Adama Maiga, Mahamadou
Coutier-Delgosha, Olivier
and
Buisine, Daniel
2018.
Analysis of the critical pressure of cavitation bubbles.
Meccanica,
Vol. 53,
Issue. 4-5,
p.
787.
Ye, Linzheng
Zhu, Xijing
and
Liu, Yao
2019.
Numerical study on dual-frequency ultrasonic enhancing cavitation effect based on bubble dynamic evolution.
Ultrasonics Sonochemistry,
Vol. 59,
Issue. ,
p.
104744.
Zhang, Shaofeng
Li, Xiaojun
Hu, Bo
Liu, Yang
and
Zhu, Zuchao
2019.
Numerical investigation of attached cavitating flow in thermo-sensitive fluid with special emphasis on thermal effect and shedding dynamics.
International Journal of Hydrogen Energy,
Vol. 44,
Issue. 5,
p.
3170.
Huang, Y.
Wang, J.
Abe, A.
Wang, Y.
Du, T.
and
Huang, C.
2019.
A theoretical model to estimate inactivation effects of OH radicals on marine Vibrio sp. in bubble-shock interaction.
Ultrasonics Sonochemistry,
Vol. 55,
Issue. ,
p.
359.
Reuter, Fabian
and
Kaiser, Sebastian A.
2019.
High-speed film-thickness measurements between a collapsing cavitation bubble and a solid surface with total internal reflection shadowmetry.
Physics of Fluids,
Vol. 31,
Issue. 9,
Zhang, Jing
Zhang, Lingxin
and
Deng, Jian
2019.
Numerical Study of the Collapse of Multiple Bubbles and the Energy Conversion during Bubble Collapse.
Water,
Vol. 11,
Issue. 2,
p.
247.
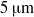 $5~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. Water is opaque to the infrared light spectrum, hence only temperatures in the boundary layer and on the liquid vapour interface could be determined. A temperature decrease of
$5~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. Water is opaque to the infrared light spectrum, hence only temperatures in the boundary layer and on the liquid vapour interface could be determined. A temperature decrease of 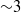 ${\sim }3$ K was recorded during the bubble growth while an increase up to 4 K was detected during the collapse. Experimental results are compared to the predictions of the ‘thermal delay’ model based on the assumption that the bubble growth and collapse are due to phase changes only. In this approach, the temperature variations are related to the latent heat exchanges during the vapourization and condensation processes. On the basis of these results, the respective effects of phase change and air dilatation/compression in the bubble dynamics are discussed.
${\sim }3$ K was recorded during the bubble growth while an increase up to 4 K was detected during the collapse. Experimental results are compared to the predictions of the ‘thermal delay’ model based on the assumption that the bubble growth and collapse are due to phase changes only. In this approach, the temperature variations are related to the latent heat exchanges during the vapourization and condensation processes. On the basis of these results, the respective effects of phase change and air dilatation/compression in the bubble dynamics are discussed.

