Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Melnikov, D. E.
Pushkin, D. O.
and
Shevtsova, V. M.
2013.
Synchronization of finite-size particles by a traveling wave in a cylindrical flow.
Physics of Fluids,
Vol. 25,
Issue. 9,
Lappa, Marcello
2013.
On the variety of particle accumulation structures under the effect of g-jitters.
Journal of Fluid Mechanics,
Vol. 726,
Issue. ,
p.
160.
Legros, J. C.
Gaponenko, Yu.
Lyubimova, T.
and
Shevtsova, V.
2014.
Soret separation in a binary liquid mixture near its critical temperature.
The European Physical Journal E,
Vol. 37,
Issue. 10,
Melnikov, D.E.
and
Shevtsova, V.M.
2014.
The effect of ambient temperature on the stability of thermocapillary flow in liquid column.
International Journal of Heat and Mass Transfer,
Vol. 74,
Issue. ,
p.
185.
Watanabe, T.
Melnikov, D. E.
Matsugase, T.
Shevtsova, V.
and
Ueno, I.
2014.
The Stability of a Thermocapillary-Buoyant Flow in a Liquid Bridge with Heat Transfer Through the Interface.
Microgravity Science and Technology,
Vol. 26,
Issue. 1,
p.
17.
Ferrera, C.
Herrada, M. A.
Montanero, J. M.
Torregrosa, M.
and
Shevtsova, V.
2014.
Dynamical response of liquid bridges to a step change in the mass force magnitude.
Physics of Fluids,
Vol. 26,
Issue. 1,
Yano, T.
Nishino, K.
Kawamura, H.
Ueno, I.
and
Matsumoto, S.
2015.
Instability and associated roll structure of Marangoni convection in high Prandtl number liquid bridge with large aspect ratio.
Physics of Fluids,
Vol. 27,
Issue. 2,
Karbaschi, M.
Taeibi Rahni, M.
Javadi, A.
Cronan, C.L.
Schano, K.H.
Faraji, S.
Won, J.Y.
Ferri, J.K.
Krägel, J.
and
Miller, R.
2015.
Dynamics of drops — Formation, growth, oscillation, detachment, and coalescence.
Advances in Colloid and Interface Science,
Vol. 222,
Issue. ,
p.
413.
Melnikov, D.E.
Shevtsova, V.
Yano, T.
and
Nishino, K.
2015.
Modeling of the experiments on the Marangoni convection in liquid bridges in weightlessness for a wide range of aspect ratios.
International Journal of Heat and Mass Transfer,
Vol. 87,
Issue. ,
p.
119.
Liang, Ruquan
Yan, Fuqiang
Li, Xiaoyuan
Zhang, Shuo
Yang, Shuo
Chang, G.A.
Ma, M.
Arumuga Perumal, S.
and
Chen, G.
2016.
Effects of external environment on thermocapillary convection of high prandtl number fluid.
MATEC Web of Conferences,
Vol. 40,
Issue. ,
p.
06003.
Yano, Taishi
Maruyama, Kaname
Matsunaga, Takuya
and
Nishino, Koichi
2016.
Effect of ambient gas flow on the instability of Marangoni convection in liquid bridges of various volume ratios.
International Journal of Heat and Mass Transfer,
Vol. 99,
Issue. ,
p.
182.
Yang, Shuo
Liang, Ruquan
Wang, Guofeng
Gao, Yu
Ma, Rui
Xu, Youning
and
Xia, Yongfang
2018.
The experimental investigation on dynamic response of free surface for non-isothermal liquid bridge with the varying shear airflow.
Experimental Thermal and Fluid Science,
Vol. 98,
Issue. ,
p.
662.
Yano, Taishi
Hirotani, Makoto
and
Nishino, Koichi
2018.
Effect of interfacial heat transfer on basic flow and instability in a high-Prandtl-number thermocapillary liquid bridge.
International Journal of Heat and Mass Transfer,
Vol. 125,
Issue. ,
p.
1121.
Rajasekharan, Jayakrishnan
and
Tiwari, Shaligram
2018.
Effect of an air stream along concave interface on flow and heat transfer characteristics in liquid bridges.
Vol. 1978,
Issue. ,
p.
030006.
Jayakrishnan, R.
and
Tiwari, Shaligram
2018.
Effect of Ambient Conditions on Flow and Heat Transfer in a Liquid Bridge.
Journal of Thermophysics and Heat Transfer,
Vol. 32,
Issue. 2,
p.
380.
Yasnou, V.
Gaponenko, Y.
Mialdun, A.
and
Shevtsova, V.
2018.
Influence of a coaxial gas flow on the evolution of oscillatory states in a liquid bridge.
International Journal of Heat and Mass Transfer,
Vol. 123,
Issue. ,
p.
747.
Ibrahim-Rassoul, N.
Si-Ahmed, E.-K.
Serir, A.
Kessi, A.
Legrand, J.
and
Djilali, N.
2019.
Investigation of Two-Phase Flow in a Hydrophobic Fuel-Cell Micro-Channel.
Energies,
Vol. 12,
Issue. 11,
p.
2061.
Shitomi, Nobuhiro
Yano, Taishi
and
Nishino, Koichi
2019.
Effect of radiative heat transfer on thermocapillary convection in long liquid bridges of high-Prandtl-number fluids in microgravity.
International Journal of Heat and Mass Transfer,
Vol. 133,
Issue. ,
p.
405.
Jayakrishnan, R.
and
Tiwari, Shaligram
2019.
Influence of co-axial airflow and volume ratio on thermo-capillary convection in half floating zones.
Computers & Fluids,
Vol. 179,
Issue. ,
p.
248.
Yano, Taishi
and
Nishino, Koichi
2020.
Numerical study on the effects of convective and radiative heat transfer on thermocapillary convection in a high-Prandtl-number liquid bridge in weightlessness.
Advances in Space Research,
Vol. 66,
Issue. 8,
p.
2047.
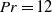 $\mathit{Pr}= 12$ (
$\mathit{Pr}= 12$ ( $n$-decane) and
$n$-decane) and 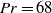 $\mathit{Pr}= 68$ (5 cSt silicone oil) when the interface is subjected to an axial gas stream. The gas flow is co- or counter-directed with respect to the Marangoni flow. In the case when the gas stream comes from the cold side, it cools down the interface to a temperature lower than that of the liquid beneath and in a certain region of the parameter space that cooling causes an instability due to a temperature difference in the direction perpendicular to the interface. The disturbances are swept by the thermocapillary flow to the cold side, which leads to the appearance of axisymmetric waves propagating in the axial direction from the hot to cold side. The mechanism of this new two-dimensional oscillatory instability is similar to that of the Pearson’s instability of the rest state in a thin layer heated from below (Pearson, J. Fluid Mech., vol. 4, 1958, p. 489), and it appears at the value of the transverse Marangoni number
$\mathit{Pr}= 68$ (5 cSt silicone oil) when the interface is subjected to an axial gas stream. The gas flow is co- or counter-directed with respect to the Marangoni flow. In the case when the gas stream comes from the cold side, it cools down the interface to a temperature lower than that of the liquid beneath and in a certain region of the parameter space that cooling causes an instability due to a temperature difference in the direction perpendicular to the interface. The disturbances are swept by the thermocapillary flow to the cold side, which leads to the appearance of axisymmetric waves propagating in the axial direction from the hot to cold side. The mechanism of this new two-dimensional oscillatory instability is similar to that of the Pearson’s instability of the rest state in a thin layer heated from below (Pearson, J. Fluid Mech., vol. 4, 1958, p. 489), and it appears at the value of the transverse Marangoni number 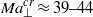 ${ \mathit{Ma}}_{\perp }^{cr} \approx 39\text{{\ndash}} 44$ lower than that of the Pearson’s instability in a horizontal layer (
${ \mathit{Ma}}_{\perp }^{cr} \approx 39\text{{\ndash}} 44$ lower than that of the Pearson’s instability in a horizontal layer (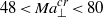 $48\lt { \mathit{Ma}}_{\perp }^{cr} \lt 80$, depending on the Biot number). The generality of the instability mechanism indicates that it is not limited to cylindrical geometry and might be observed in a liquid layer with cold gas stream.
$48\lt { \mathit{Ma}}_{\perp }^{cr} \lt 80$, depending on the Biot number). The generality of the instability mechanism indicates that it is not limited to cylindrical geometry and might be observed in a liquid layer with cold gas stream.

