Published online by Cambridge University Press: 18 December 2015
The purely conductive state in configurations such as the Rayleigh–Bénard one is linearly stable for yield stress fluids at all Rayleigh numbers, 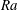 $Ra$. However, on changing to localized heater configurations the static background state exists only if the yield stress is sufficiently large. Otherwise, thermal plumes may be induced in a stationary viscoplastic fluid layer, as illustrated in the recent experimental study of Davaille et al. (J. Non-Newtonian Fluid Mech., vol. 193, 2013, 144–153). Here, we study an analogous problem both analytically and computationally, from the perspective of an ideal yield stress fluid (Bingham fluid) that is initially stationary in a locally heated rectangular tank. We show that for a non-zero yield stress the onset of flow waits for a start time
$Ra$. However, on changing to localized heater configurations the static background state exists only if the yield stress is sufficiently large. Otherwise, thermal plumes may be induced in a stationary viscoplastic fluid layer, as illustrated in the recent experimental study of Davaille et al. (J. Non-Newtonian Fluid Mech., vol. 193, 2013, 144–153). Here, we study an analogous problem both analytically and computationally, from the perspective of an ideal yield stress fluid (Bingham fluid) that is initially stationary in a locally heated rectangular tank. We show that for a non-zero yield stress the onset of flow waits for a start time 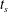 $t_{s}$ that increases with the dimensionless ratio of yield stress to buoyancy stress, denoted
$t_{s}$ that increases with the dimensionless ratio of yield stress to buoyancy stress, denoted 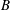 $B$. We provide a precise mathematical definition of
$B$. We provide a precise mathematical definition of 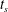 $t_{s}$ and approximately evaluate this for different values of
$t_{s}$ and approximately evaluate this for different values of 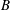 $B$, using both computational and semianalytical methods. For sufficiently large
$B$, using both computational and semianalytical methods. For sufficiently large 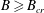 $B\geqslant B_{cr}$, the fluid is unable to yield. For the flow studied,
$B\geqslant B_{cr}$, the fluid is unable to yield. For the flow studied, 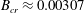 $B_{cr}\approx 0.00307$. The critical value
$B_{cr}\approx 0.00307$. The critical value 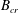 $B_{cr}$ and the start time
$B_{cr}$ and the start time 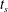 $t_{s}$, for
$t_{s}$, for 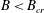 $B<B_{cr}$, are wholly independent of
$B<B_{cr}$, are wholly independent of 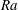 $Ra$ and
$Ra$ and 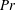 $Pr$. For
$Pr$. For 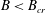 $B<B_{cr}$, yielding starts at
$B<B_{cr}$, yielding starts at 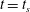 $t=t_{s}$. The flow develops into either a weakly or a strongly convective flow. In the former case the passage to a steady state is relatively smooth and monotone, resulting eventually in a steady convective plume above the heater, rising and impinging on the upper wall, then recirculating steadily around the tank. With strongly convecting flows, for progressively larger
$t=t_{s}$. The flow develops into either a weakly or a strongly convective flow. In the former case the passage to a steady state is relatively smooth and monotone, resulting eventually in a steady convective plume above the heater, rising and impinging on the upper wall, then recirculating steadily around the tank. With strongly convecting flows, for progressively larger 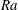 $Ra$ we observe an increasing number of distinct plume heads and a tendency for plumes to develop as short-lived pulses. Over a certain range of
$Ra$ we observe an increasing number of distinct plume heads and a tendency for plumes to develop as short-lived pulses. Over a certain range of 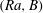 $(Ra,B)$ the flow becomes temporarily frozen between two consecutive pulses. Such characteristics are distinctly reminiscent of the experimental work of Davaille et al. (J. Non-Newtonian Fluid Mech., vol. 193, 2013, 144–153). The yield stress plays a multifaceted role here as it affects plume temperature, size and velocity through different mechanisms. On the one hand, increasing
$(Ra,B)$ the flow becomes temporarily frozen between two consecutive pulses. Such characteristics are distinctly reminiscent of the experimental work of Davaille et al. (J. Non-Newtonian Fluid Mech., vol. 193, 2013, 144–153). The yield stress plays a multifaceted role here as it affects plume temperature, size and velocity through different mechanisms. On the one hand, increasing 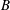 $B$ tends to increase the maximum temperature of the plume heads. On the other hand, for larger
$B$ tends to increase the maximum temperature of the plume heads. On the other hand, for larger 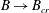 $B\rightarrow B_{cr}$, the plume never starts.
$B\rightarrow B_{cr}$, the plume never starts.