Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Scheel, Janet D
Emran, Mohammad S
and
Schumacher, Jörg
2013.
Resolving the fine-scale structure in turbulent Rayleigh–Bénard convection.
New Journal of Physics,
Vol. 15,
Issue. 11,
p.
113063.
Zhou, Quan
and
Xia, Ke-Qing
2013.
Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell.
Journal of Fluid Mechanics,
Vol. 721,
Issue. ,
p.
199.
van der Poel, Erwin P.
Stevens, Richard J. A. M.
and
Lohse, Detlef
2013.
Comparison between two- and three-dimensional Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 736,
Issue. ,
p.
177.
Xia, Ke-Qing
2013.
Current trends and future directions in turbulent thermal convection.
Theoretical and Applied Mechanics Letters,
Vol. 3,
Issue. 5,
p.
052001.
Wei, Ping
and
Xia, Ke-Qing
2013.
Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting.
Journal of Fluid Mechanics,
Vol. 720,
Issue. ,
p.
140.
Shishkina, Olga
Horn, Susanne
and
Wagner, Sebastian
2013.
Falkner–Skan boundary layer approximation in Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 730,
Issue. ,
p.
442.
Stevens, Richard J. A. M.
Lohse, Detlef
and
Verzicco, Roberto
2014.
Sidewall effects in Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 741,
Issue. ,
p.
1.
du Puits, Ronald
Li, Ling
Resagk, Christian
Thess, André
and
Willert, Christian
2014.
Turbulent Boundary Layer in High Rayleigh Number Convection in Air.
Physical Review Letters,
Vol. 112,
Issue. 12,
Mehrvarzi, C. O.
and
Paul, M. R.
2014.
Front propagation in a chaotic flow field.
Physical Review E,
Vol. 90,
Issue. 1,
Scheel, Janet D.
and
Schumacher, Jörg
2014.
Local boundary layer scales in turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
344.
van der Poel, Erwin P.
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
Grossmann, Siegfried
and
Lohse, Detlef
2015.
Logarithmic Mean Temperature Profiles and Their Connection to Plume Emissions in Turbulent Rayleigh-Bénard Convection.
Physical Review Letters,
Vol. 115,
Issue. 15,
Petschel, K.
Stellmach, S.
Wilczek, M.
Lülff, J.
and
Hansen, U.
2015.
Kinetic energy transport in Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 773,
Issue. ,
p.
395.
van der Poel, Erwin P.
Ostilla-Mónico, Rodolfo
Donners, John
and
Verzicco, Roberto
2015.
A pencil distributed finite difference code for strongly turbulent wall-bounded flows.
Computers & Fluids,
Vol. 116,
Issue. ,
p.
10.
Shishkina, Olga
Horn, Susanne
Wagner, Sebastian
and
Ching, Emily S. C.
2015.
Thermal Boundary Layer Equation for Turbulent Rayleigh–Bénard Convection.
Physical Review Letters,
Vol. 114,
Issue. 11,
Pandey, Ambrish
and
Verma, Mahendra K.
2016.
Scaling of large-scale quantities in Rayleigh-Bénard convection.
Physics of Fluids,
Vol. 28,
Issue. 9,
du Puits, R.
and
Willert, C.
2016.
The evolution of the boundary layer in turbulent Rayleigh-Bénard convection in air.
Physics of Fluids,
Vol. 28,
Issue. 4,
Wang, Yin
He, Xiaozhou
and
Tong, Penger
2016.
Boundary layer fluctuations and their effects on mean and variance temperature profiles in turbulent Rayleigh-Bénard convection.
Physical Review Fluids,
Vol. 1,
Issue. 8,
Pandey, Ambrish
Kumar, Abhishek
Chatterjee, Anando G.
and
Verma, Mahendra K.
2016.
Dynamics of large-scale quantities in Rayleigh-Bénard convection.
Physical Review E,
Vol. 94,
Issue. 5,
Sakievich, P.J.
Peet, Y.T.
and
Adrian, R.J.
2016.
Large-scale thermal motions of turbulent Rayleigh–Bénard convection in a wide aspect-ratio cylindrical domain.
International Journal of Heat and Fluid Flow,
Vol. 61,
Issue. ,
p.
183.
Ovsyannikov, Mikhail
Krasnov, Dmitry
Emran, Mohammad S.
and
Schumacher, Jörg
2016.
Combined effects of prescribed pressure gradient and buoyancy in boundary layer of turbulent Rayleigh–Bénard convection.
European Journal of Mechanics - B/Fluids,
Vol. 57,
Issue. ,
p.
64.
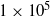 to
to 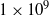 . Detailed measurements of the thermal and viscous boundary layer profiles are made and compared to experimental and theoretical (Prandtl–Blasius) results. We find that the thermal boundary layer profiles disagree by more than 10 % when scaled with the similarity variable (boundary layer thickness) and likewise disagree with the Prandtl–Blasius results. In contrast, the viscous boundary profiles collapse well and do agree (within 10 %) with the Prandtl–Blasius profile, but with worsening agreement as the Rayleigh number increases. We have also investigated the scaling of the boundary layer thicknesses with Rayleigh number, and again compare to experiments and theory. We find that the scaling laws are very robust with respect to method of analysis and they mostly agree with the Grossmann–Lohse predictions coupled with laminar boundary layer theory within our numerical uncertainty.
. Detailed measurements of the thermal and viscous boundary layer profiles are made and compared to experimental and theoretical (Prandtl–Blasius) results. We find that the thermal boundary layer profiles disagree by more than 10 % when scaled with the similarity variable (boundary layer thickness) and likewise disagree with the Prandtl–Blasius results. In contrast, the viscous boundary profiles collapse well and do agree (within 10 %) with the Prandtl–Blasius profile, but with worsening agreement as the Rayleigh number increases. We have also investigated the scaling of the boundary layer thicknesses with Rayleigh number, and again compare to experiments and theory. We find that the scaling laws are very robust with respect to method of analysis and they mostly agree with the Grossmann–Lohse predictions coupled with laminar boundary layer theory within our numerical uncertainty.

