Published online by Cambridge University Press: 10 May 2009
Heterogeneous condensation of vapours mixed with a carrier gas in the stagnation point boundary layer flow near a cold wall is considered in the presence of solid particles much larger than the mean free path of vapour particles. The supersaturated vapour condenses on the particles by diffusion, and particles and droplets are thermophoretically attracted to the wall. Assuming that the heat of vaporization is much larger than kB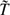 ∞, where
∞, where 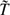 ∞ is the temperature far from the wall, vapour condensation occurs in a condensation layer (CL). The CL width and characteristics depend on the parameters of the problem, and a parameter R yielding the rate of vapour scavenging by solid particles is particularly important. Assuming that the CL is so narrow that temperature, particle density and velocity do not change appreciably inside it, an asymptotic theory is found, the δ-CL theory, that approximates very well the vapour and droplet profiles, the dew point shift and the deposition rates at the wall for wide ranges of the wall temperature
∞ is the temperature far from the wall, vapour condensation occurs in a condensation layer (CL). The CL width and characteristics depend on the parameters of the problem, and a parameter R yielding the rate of vapour scavenging by solid particles is particularly important. Assuming that the CL is so narrow that temperature, particle density and velocity do not change appreciably inside it, an asymptotic theory is found, the δ-CL theory, that approximates very well the vapour and droplet profiles, the dew point shift and the deposition rates at the wall for wide ranges of the wall temperature 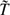 w and the scavenging parameter R. This theory breaks down for
w and the scavenging parameter R. This theory breaks down for 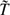 w very close to the maximum temperature yielding non-zero droplet deposition rate,
w very close to the maximum temperature yielding non-zero droplet deposition rate, 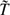 w, M. If the width of the CL is assumed to be zero (0-CL theory), the vapour density reaches local equilibrium with the condensate immediately after it enters the dew surface. The 0-CL theory yields appropriate profiles and deposition rates in the limit as R → ∞ and also for any R, provided
w, M. If the width of the CL is assumed to be zero (0-CL theory), the vapour density reaches local equilibrium with the condensate immediately after it enters the dew surface. The 0-CL theory yields appropriate profiles and deposition rates in the limit as R → ∞ and also for any R, provided 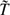 w is very close to
w is very close to 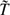 w, M. Nonlinear multiple scales also improve the 0-CL theory, providing good uniform approximations to the deposition rates and the profiles for large R or for moderate R and
w, M. Nonlinear multiple scales also improve the 0-CL theory, providing good uniform approximations to the deposition rates and the profiles for large R or for moderate R and 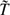 w very close to
w very close to 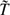 w, M, but it breaks down for other values of
w, M, but it breaks down for other values of 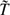 w and small R.
w and small R.