Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-04T21:11:52.211Z Has data issue: false hasContentIssue false
  • English
  • Français

A theory for the streamwise turbulent fluctuations in high Reynolds number pipe flow

Published online by Cambridge University Press:  24 July 2012

Marcus Hultmark
Marcus Hultmark*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA School of Architecture, Civil and Environmental Engineering, École Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A new theory for the streamwise turbulent fluctuations in fully developed pipe flow is proposed. The theory extends the similarities between the mean flow and the streamwise turbulence fluctuations, as observed in experimental high Reynolds number data, to also include the theoretical derivation. Connecting the derivation of the fluctuations to that of the mean velocity at finite Reynolds number as introduced by Wosnik, Castillo & George (J. Fluid Mech., vol. 421, 2000, pp. 115–145) can explain the logarithmic behaviour as well as the coefficient of the logarithm. The slope of the logarithm, for the fluctuations, depends on the increase of the fluctuations with Reynolds number, which is shown to agree very well with the experimental data. 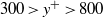A mesolayer, similar to that introduced by Wosnik et al., exists for the fluctuations for , which coincides with the mesolayer for the mean velocities. In the mesolayer, the flow is still affected by viscosity, which shows up as a decrease in the fluctuations.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 575 - 584
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bailey, S. C. C, Kunkel, G. J., Hultmark, M., Vallikivi, M., Hill, J. P., Meyer, K. A., Tsay, C., Arnold, C. B. & Smits, A. J. 2010 Turbulence measurements using a nanoscale thermal anemometry probe. J. Fluid Mech. 663, 160–179.CrossRefGoogle Scholar
2. Castillo, L. 1997Similarity analysis of turbulent boundary layers. PhD thesis, State University of New York at Buffalo.Google Scholar
3. Frisch, U. & Orszag, S. A. 1990 Turbulence: challenges for theory and experiment. Phys. Today 43 (1), 24–32.CrossRefGoogle Scholar
4. George, W. K. 1988 Another look at the log (or is it a power law?) velocity profile for a zero-pressure gradient boundary layer.. Bull. Am. Phys. Soc. 33 (10), 2301.Google Scholar
5. George, W. K. 2007 Is there a universal log law for turbulent wall-bounded flows?. Phil. Trans. R. Soc. Lond. A 365, 789–806.Google Scholar
6. George, W. K. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.CrossRefGoogle Scholar
7. Hultmark, M. N., Bailey, S. C. C. & Smits, A. J. 2010 Scaling of near-wall turbulence in pipe flow. J. Fluid Mech. 649, 103–113.CrossRefGoogle Scholar
8. Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.CrossRefGoogle ScholarPubMed
9. Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
10. McKeon, B. J., Li, J., Jiang, W., Morrison, J. F. & Smits, A. J. 2004 Further observations on the mean velocity distribution in fully developed pipe flow. J. Fluid Mech. 501, 135–147.CrossRefGoogle Scholar
11. Millikan, C. B. 1939 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress of Applied Mechanics. Cambridge, MA.Google Scholar
12. Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.CrossRefGoogle Scholar
13. Perry, A. E., Henbest, S. M. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
14. Smits, A. J. (Ed.) 1991 Proceedings of the Princeton Workshop on New Approaches to Experimental Turbulence Research. Princeton, NJ.Google Scholar
15. Smits, A. J., Monty, J., Hultmark, M., Bailey, S. C. C., Hutchins, M. & Marusic, I. 2011 Spatial resolution correction for turbulence measurements. J. Fluid Mech. 676, 41–53.CrossRefGoogle Scholar
16. Squire, H. B. 1948 I. reconsideration of the theory of free turbulence. Phil. Mag. (7) 39 (288), 1–20.CrossRefGoogle Scholar
17. Stanton, T. E. & Pannell, F. R. S. 1914 Similarity of motion in relation to the surface friction of fluids. Phil. Trans. R. Soc. Lond. A 214, 199–212.Google Scholar
18. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
19. Vallikivi, M., Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2011 Turbulence measurements in pipe flow using a nano-scale thermal anemometry probe. Exp. Fluids 51, 1521–1527.CrossRefGoogle Scholar
20. Wosnik, M. 2000On wall-bounded turbulent shear flows. PhD thesis, State University of New York at Buffalo.Google Scholar
21. Wosnik, M., Castillo, L. & George, W. K. 2000 A theory for turbulent pipe and channel flows. J. Fluid Mech. 421, 115–145.CrossRefGoogle Scholar
22. Zagarola, M. V. 1996Mean-flow scaling of turbulent pipe flow. PhD thesis, Princeton University.Google Scholar
23. Zagarola, M. V. & Smits, A. J. 1997 Log laws or power laws: the scaling in the overlap region. Phys. Fluids 9, 2094.CrossRefGoogle Scholar
24. Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar