Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T09:19:04.077Z Has data issue: false hasContentIssue false
  • English
  • Français

A tent model of vortex reconnection under Biot–Savart evolution

Published online by Cambridge University Press:  17 November 2017

Yoshifumi Kimura  and
H. K. Moffatt Open the ORCID record for H. K. Moffatt [Opens in a new window]
Yoshifumi Kimura
Affiliation:
Graduate School of Mathematics, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8602, Japan
H. K. Moffatt*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Vortex reconnection under Biot–Savart evolution is investigated geometrically and numerically using a tent model consisting of vortex filaments initially in the form of two tilted hyperbolic branches; the vortices are antiparallel at their points of nearest approach. It is shown that the tips of these vortices approach each other, accelerating as they do so to form a finite-time singularity at the apex of the tent. The minimum separation of the vortices and the maximum velocity and axial strain rate exhibit nearly self-similar Leray scaling, but the exponents of the velocity and strain rate deviate slightly from their respective self-similar values of 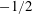$-1/2$ and 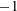$-1$; this deviation is associated with the appearance of distinct minima of curvature leading to cusp structures at the tips. The writhe and twist of each vortex are both zero at all times up to the instant of reconnection. By way of validation of the model, the structure of the eigenvalues and eigenvectors of the rate-of-strain tensor is investigated: it is shown that the second eigenvalue 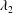$\unicode[STIX]{x1D706}_{2}$ has dipole structure around the vortex filaments. At the tips, it is observed that 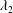$\unicode[STIX]{x1D706}_{2}$ is positive and the corresponding eigenvector is tangent to the filament, implying persistent stretching of the vortex.

JFM classification

Mathematical Foundations: Mathematical Foundations Mathematical Foundations: Topological fluid dynamics Vortex Flows: Vortex interactions
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 834 , 10 January 2018 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bewley, G. P., Paoletti, M. S., Sreenivasan, K. P. & Lathrop, D. P. 2008 Characterization of reconnecting vortices in superfluid helium. Proc. Natl Acad. Sci. USA 105 (37), 13707–13710.CrossRefGoogle ScholarPubMed
Boué, L., Khomenko, D., L’vov, V. S. & Procaccia, I. 2013 Analytic solution of the approach of quantum reconnection. Phys. Rev. Lett. 111, 145301.CrossRefGoogle ScholarPubMed
Brenner, M. P., Hormoz, S. & Pumir, A. 2016 Potential singularity mechanism for the Euler equations. Phys. Rev. Fluids 1, 084503.CrossRefGoogle Scholar
Fonda, E., Meichie, D. P., Ouellette, N., Hormoz, S. & Lathrop, D. P. 2014 Direct observation of Kelvin waves excited by quantized vortex reconnection. Proc. Natl Acad. Sci. USA 111 (Supplement 1), 4707–4710.CrossRefGoogle ScholarPubMed
Hussain, F. & Duraisamy, K. 2011 Mechanics of viscous vortex reconnection. Phys. Fluids 23, 021701.CrossRefGoogle Scholar
Kida, S. & Takaoka, M. 1994 Vortex reconnection. Annu. Rev. Fluid Mech. 26, 169–189.CrossRefGoogle Scholar
Kimura, Y. & Moffatt, H. K. 2014 Reconnection of skewed vortices. J. Fluid Mech. 751, 329–345.CrossRefGoogle Scholar
Kimura, Y. & Moffatt, H. K. 2017 [KM17] Scaling properties towards vortex reconnection under Biot–Savart evolution. Fluid Dyn. Res.; doi:10.1088/1873-7005/aa710c.Google Scholar
Kleckner, D. & Irvine, W. T. M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9, 253258.CrossRefGoogle Scholar
Leray, J. 1934 Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 63, 193–248.CrossRefGoogle Scholar
Moffatt, H. K. & Ricca, R. L. 1992 Helicity and the Călugăreanu invariant. Proc. R. Soc. Lond. A 439, 411–429.Google Scholar
Moffatt, H. K., Kida, S. & Ohkitani, K. 1994 Stretched vortices – the sinews of turbulence; large-Reynolds-number asymptotics. J. Fluid Mech. 259, 241–264.CrossRefGoogle Scholar
Rorai, C., Skipper, J., Kerr, R. M. & Sreenivasan, K. R. 2016 Approach and separation of quantized vortices with balanced cores. J. Fluid Mech. 808, 641–667.CrossRefGoogle Scholar
Serafini, S., Galantucci, L., Iseni, E., Bienaimé, T., Bisset, R. N., Barenghi, C. B., Dalfovo, F., Lamporesi, G. & Ferrari, G. 2017 Vortex reconnections and rebounds in trapped atomic Bose-Einstein condensates. Phys. Rev. X 7 (2), 021031.Google Scholar
Tebbs, R., Youd, A. J. & Barenghi, C. F. 2011 The approach to vortex reconnections. J. Low Temp. Phys. 162, 314–321.CrossRefGoogle Scholar
Villois, A., Proment, D. & Krstulovic, G. 2017 Universal and non-universal aspects of vortex reconnections in superfluids. Phys. Rev. Fluids 2, 044701.CrossRefGoogle Scholar
de Waele, A. T. A. M. & Aarts, R. G. K. M. 1994 Route to vortex reconnection. Phys. Rev. Lett. 72, 482–485.CrossRefGoogle Scholar
Zuccher, S., Caliari, M., Baggaley, A. W. & Barenghi, C. F. 2012 Quantum vortex reconnections. Phys. Fluids 24, 125108.CrossRefGoogle Scholar

Kimura et al. supplementary movie 1

Vortex evolution for the tent model; n=4096

Download Kimura et al. supplementary movie 1(Video)
Video 6.1 MB

Kimura et al. supplementary movie 2

Tent model evolution of single vortex, n=4096

Download Kimura et al. supplementary movie 2(Video)
Video 3.8 MB