Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T01:55:22.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Temporal stability of eccentric Taylor–Couette–Poiseuille flow

Published online by Cambridge University Press:  19 September 2013

Colin Leclercq ,
Benoît Pier  and
Julian F. Scott
Colin Leclercq*
Affiliation:
Laboratoire de mécanique des fluides et d’acoustique, École centrale de Lyon – CNRS – Université Claude-Bernard Lyon 1 – INSA Lyon, 36 avenue Guy-de-Collongue, 69134 Écully CEDEX, France
Benoît Pier
Affiliation:
Laboratoire de mécanique des fluides et d’acoustique, École centrale de Lyon – CNRS – Université Claude-Bernard Lyon 1 – INSA Lyon, 36 avenue Guy-de-Collongue, 69134 Écully CEDEX, France
Julian F. Scott
Affiliation:
Laboratoire de mécanique des fluides et d’acoustique, École centrale de Lyon – CNRS – Université Claude-Bernard Lyon 1 – INSA Lyon, 36 avenue Guy-de-Collongue, 69134 Écully CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The combined effects of axial flow and eccentricity on the temporal stability properties of the Taylor–Couette system are investigated using a pseudospectral method. Eccentricity is found to stabilize the Couette flow regardless of axial advection intensity. As the axial Reynolds number 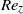${\mathit{Re}}_{z} $ is increased for any fixed eccentricity 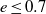$e\leq 0. 7$, the critical mode switches from deformed toroidal Taylor vortices to helical structures with an increasing number of waves, and with helicity opposed to the inner-cylinder rotation. For a wide-gap configuration of radius ratio 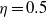$\eta = 0. 5$, increasing axial advection has a stabilizing effect for low 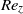${\mathit{Re}}_{z} $, then a weak destabilizing effect for high enough 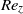${\mathit{Re}}_{z} $. Centrifugal effects are always destabilizing, but axial shear is responsible for the dominance of helical modes of increasing azimuthal complexity. The modes localize in the converging gap region, and the energy concentrates increasingly into axial motion for larger 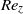${\mathit{Re}}_{z} $. Critical quantities are also computed for a small-gap case, and similar trends are observed, even though no destabilizing effect of advection is observed within the range of 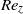${\mathit{Re}}_{z} $ considered. Comparison with the experiment of Coney & Mobbs (Proc. Inst. Mech. Engrs, vol. 184 Pt 3L, 1969–70, pp. 10–17) for 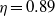$\eta = 0. 89$ shows good agreement, despite small discrepancies attributed to finite length effects.

JFM classification

Convection: Convection Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 68 - 99
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altmeyer, S., Hoffmann, C. & Lücke, M. 2011 Islands of instability for growth of spiral vortices in the Taylor–Couette system with and without axial through flow. Phys. Rev. E 84, 046308.Google Scholar
Arnoldi, W. E. 1951 The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q. Appl. Maths 9, 17–29.Google Scholar
Babcock, K. L., Ahlers, G. & Cannell, D. S. 1991 Noise-sustained structure in Taylor–Couette flow with through flow. Phys. Rev. Lett. 67, 3388–3391.Google Scholar
Babcock, K. L., Cannell, D. S. & Ahlers, G. 1992 Stability and noise in Taylor–Couette flow with through-flow. Physica D 61 (1), 40–46.Google Scholar
Castle, P. & Mobbs, F. R. 1967 Hydrodynamic stability of the flow between eccentric rotating cylinders: visual observations and torque measurements (paper 6). In Institution of Mechanical Engineers, Conference Proceedings, vol. 182, pp. 41–52.Google Scholar
Chandrasekhar, S. 1960 The hydrodynamic stability of viscid flow between coaxial cylinders. Proc. Natl Acad. Sci. USA 46, 141–143.Google Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Chawda, A. & Avgousti, M. 1996 Stability of viscoelastic flow between eccentric rotating cylinders. J. Non-Newtonian Fluid Mech. 63, 97–120.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Cole, J. A. 1957 Experiments on the flow in rotating annular clearances (paper 15). In Proceedings of the Conference on Lubrication and Wear, pp. 16–19. Institution of Mechanical Engineers.Google Scholar
Cole, J. A. 1967 Taylor vortices with eccentric rotating cylinders. Nature 216, 1200–1202.CrossRefGoogle Scholar
Cole, J. A. 1969 Taylor vortices with eccentric rotating cylinders. Nature 221, 253–254.Google Scholar
Coney, J. E. R. 1971 Taylor vortex flow with special reference to rotary heat exchangers. PhD thesis, University of Leeds.Google Scholar
Coney, J. E. R. & Atkinson, J. 1978 The effect of Taylor vortex flow on the radial forces in an annulus having variable eccentricity and axial flow. Trans. ASME: J. Fluids Engng 100, 210–214.Google Scholar
Coney, J. E. R & Mobbs, F. R. 1969–70 Hydrodynamic stability of the flow between eccentric rotating cylinders with axial flow: visual observations (paper 2). Proc. Inst. Mech. Engrs 184 Pt 3L, 10–17.Google Scholar
Cotrell, D. L. & Pearlstein, A. J. 2004 The connection between centrifugal instability and Tollmien–Schlichting-like instability for spiral Poiseuille flow. J. Fluid Mech. 509, 331–351.Google Scholar
Cotrell, D. L., Sarma, L. R. & Pearlstein, A. J. 2004 Computational assessment of subcritical and delayed onset in spiral Poiseuille flow experiments. J. Fluid Mech. 509, 353–378.Google Scholar
Dai, R.-X., Dong, Q. & Szeri, A. Z. 1992 Flow between eccentric rotating cylinders: bifurcation and stability. Intl J. Engng Sci. 30, 1323–1340.Google Scholar
DiPrima, R. C. 1959 The stability of viscous flow between rotating concentric cylinders with a pressure gradient acting round the cylinders. J. Fluid Mech. 6, 462–468.Google Scholar
DiPrima, R. C. 1960 The stability of a viscous fluid between rotating cylinders with an axial flow. J. Fluid Mech. 9, 621–631.Google Scholar
DiPrima, R. C. 1963 A note on the stability of flow in loaded journal bearings. Trans. Am. Soc. Lubric. Engrs 6, 249–253.Google Scholar
DiPrima, R. C., Eagles, P. M. & Ng, B. S. 1984 The effect of radius ratio on the stability of Couette flow and Taylor vortex flow. Phys. Fluids 27, 2403–2411.Google Scholar
DiPrima, R. C. & Stuart, J. T. 1972a Flow between eccentric rotating cylinders. J. Lubric. Tech. 94, 266–274.Google Scholar
DiPrima, R. C. & Stuart, J. T. 1972b Non-local effects in the stability of flow between eccentric rotating cylinders. J. Fluid Mech. 54, 393–415.Google Scholar
DiPrima, R. C. & Stuart, J. T. 1975 The nonlinear calculation of Taylor vortex flow between eccentric rotating cylinders. J. Fluid Mech. 67, 85–111.Google Scholar
Dris, I. M. & Shaqfeh, E. S. G. 1998 Experimental and theoretical observations of elastic instabilities in eccentric cylinder flows: local versus global instability. J. Non-Newtonian Fluid Mech. 80, 1–58.Google Scholar
Eagles, P. M., Stuart, J. T. & DiPrima, R. C. 1978 The effects of eccentricity on torque and load in Taylor-vortex flow. J. Fluid Mech. 87, 209–231.Google Scholar
El-Dujaily, M. J. & Mobbs, F. R. 1990 The effect of end walls on subcritical flow between concentric and eccentric rotating cylinders. Intl J. Heat Fluid Flow 11, 72–78.Google Scholar
Escudier, M. P., Gouldson, I. W., Oliveira, P. J. & Pinho, F. T. 2000 Effects of inner cylinder rotation on laminar flow of a Newtonian fluid through an eccentric annulus. Intl J. Heat Fluid Flow 21, 92–103.Google Scholar
Escudier, M. P., Oliveira, P. J. & Pinho, F. T. 2002 Fully developed laminar flow of purely viscous non-Newtonian liquids through annuli, including the effects of eccentricity and inner-cylinder rotation. Intl J. Heat Fluid Flow 23, 52–73.Google Scholar
Feng, S. & Fu, S. 2007 Influence of orbital motion of inner cylinder on eccentric Taylor vortex flow of Newtonian and power-law fluids. Chin. Phys. Lett. 24, 759–762.Google Scholar
Feng, S., Li, Q. & Fu, S. 2007 On the orbital motion of a rotating inner cylinder in annular flow. Intl J. Numer. Meth. Fluids 54, 155–173.Google Scholar
Frêne, J. & Godet, M. 1971 Transition from laminar to Taylor vortex flow in journal bearings. Tribology 4, 216–217.Google Scholar
Gaster, M. 1962 A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability. J. Fluid Mech. 14, 222–224.Google Scholar
Goda, K. 1979 A multistep technique with implicit difference schemes for calculating two- or three-dimensional cavity flows. J. Comput. Phys. 30, 76–95.Google Scholar
Guo, B. & Liu, G. 2011 Applied Drilling Circulation Systems – Hydraulics, Calculations, Models. Elsevier.Google Scholar
Heaton, C. J. 2008 Optimal linear growth in spiral Poiseuille flow. J. Fluid Mech. 607, 141–166.Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–68.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid. Mech. 22, 473–537.Google Scholar
Huggins, N. J. 1966–67 Tests on a 24-in diameter journal bearing: transition from laminar to turbulent flow. In Symposium on Journal Bearings for Reciprocating and Turbo Machinery, Proc. Inst. Mech. Engrs, vol. 181 (Pt 3B), p. 81.Google Scholar
Hwang, J. Y. & Yang, K. S. 2004 Numerical study of Taylor–Couette flow with an axial flow. Comput. Fluids 33, 97–118.Google Scholar
Kamal, M. M. 1966 Separation in the flow between eccentric rotating cylinders. Trans. ASME J. Basic Engng 88, 717–724.CrossRefGoogle Scholar
Karasudani, T. 1987 Non-axis-symmetric Taylor vortex flow in eccentric rotating cylinders. J. Phys. Soc. Japan 56, 855–858.Google Scholar
Koschmieder, E. L. 1976 Taylor vortices between eccentric cylinders. Phys. Fluids 19, 1–4.Google Scholar
Lim, T. T. & Lim, S. S. 2008 Modified expression for critical Reynolds number in eccentric Taylor–Couette flow. AIAA J. 46, 277–280.Google Scholar
Mackrodt, P. A. 1976 Stability of Hagen–Poiseuille flow with superimposed rigid rotation. J. Fluid Mech. 73, 153–164.Google Scholar
Marques, F. & Lopez, J. M. 2000 Spatial and temporal resonances in a periodically forced hydrodynamic system. Physica D 136, 340–352.CrossRefGoogle Scholar
Martinand, D., Serre, E. & Lueptow, R. M. 2009 Absolute and convective instability of cylindrical Couette flow with axial and radial flows. Phys. Fluids 21, 104102.Google Scholar
Merzari, E., Wang, S., Ninokata, H. & Theofilis, V. 2008 Biglobal linear stability analysis for the flow in eccentric annular channels and a related geometry. Phys. Fluids 20, 114104.Google Scholar
Meseguer, A. & Marques, F. 2000 On the competition between centrifugal and shear instability in spiral Couette flow. J. Fluid Mech. 402, 33–56.Google Scholar
Meseguer, A. & Marques, F. 2002 On the competition between centrifugal and shear instability in spiral Poiseuille flow. J. Fluid Mech. 455, 129–148.Google Scholar
Mobbs, F. R. & Ozogan, M. S. 1984 Study of sub-critical Taylor vortex flow between eccentric rotating cylinders by torque measurements and visual observations. Intl J. Heat Fluid Flow 5, 251–253.Google Scholar
Mobbs, F. R. & Younes, M. A. M. A. 1974 The Taylor vortex regime in the flow between eccentric rotating cylinders. Trans. ASME: J. Lubric. Tech. 127–134.Google Scholar
Nagib, H. 1972 On instabilities and secondary motions in swirling flows through annuli. PhD thesis, Illinois Institute of Technology.Google Scholar
Ng, B. S. & Turner, E. R. 1982 On the linear stability of spiral flow between rotating cylinders. Proc. R. Soc. Lond. A Mat. 382, 83–102.Google Scholar
Oikawa, M., Karasudani, T. & Funakoshi, M. 1989a Stability of flow between eccentric rotating cylinders. J. Phys. Soc. Japan 58, 2355–2364.Google Scholar
Oikawa, M., Karasudani, T. & Funakoshi, M. 1989b Stability of flow between eccentric rotating cylinders with a wide gap. J. Phys. Soc. Japan 58, 2209–2210.Google Scholar
Podryabinkin, E. V. & Rudyak, V. Y. 2011 Moment and forces exerted on the inner cylinder in eccentric annular flow. J. Engng Thermophys. 20, 320–328.Google Scholar
Raspo, I., Hugues, S., Serre, E., Randriamampianina, A. & Bontoux, P. 2002 A spectral projection method for the simulation of complex three-dimensional rotating flows. Comput. Fluids 31, 745–767.Google Scholar
Reid, W. H. 1961 Review of The hydrodynamic stability of viscid flow between coaxial cylinders by S. Chandrasekhar (Proc. Natl Acad. Sci. USA 46, 141–143, 1960). Math. Rev. 22, 565.Google Scholar
Ritchie, G. S. 1968 On the stability of viscous flow between eccentric rotating cylinders. J. Fluid Mech. 32, 131–144.Google Scholar
Sep, J. 2008 Journal bearing with an intensive axial oil flow–experimental investigation. Scientific Problems of Machines Operation and Maintenance 43, 21–29.Google Scholar
Snyder, H. A. 1962 Experiments on the stability of spiral flow at low axial Reynolds numbers. Proc. R. Soc. Lond. A Mat. 265, 198–214.Google Scholar
Snyder, H. A. 1965 Experiments on the stability of two types of spiral flow. Ann. Phys. 31, 292–313.Google Scholar
Takeuchi, D. I. & Jankowski, D. F. 1981 Numerical and experimental investigation of the stability of spiral Poiseuille flow. J. Fluid Mech. 102, 101–26.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. 223, 289–343.Google Scholar
Versteegen, P. L. & Jankowski, D. F. 1969 Experiments on the stability of viscous flow between eccentric rotating cylinders. Phys. Fluids 12, 1138–1143.Google Scholar
Vohr, J. A. 1968 An experimental study of Taylor vortices and turbulence in flow between eccentric rotating cylinders. Trans. ASME: J. Lubric. Tech. 90, 285–296.Google Scholar
Wannier, G. H. 1950 A contribution to the hydrodynamics of lubrication. Q. Appl. Maths 8, 1–32.Google Scholar
Whitham, G. B. 1963 The Navier–Stokes equations of motion. In Laminar boundary layers (ed. Rosenhead, L.), chap. III, Clarendon.Google Scholar
Wood, W. W. 1957 The asymptotic expansions at large Reynolds numbers for steady motion between noncoaxial rotating cylinders. J. Fluid Mech. 3, 159–175.Google Scholar
Xiao, Q., Lim, T. T. & Chew, Y. T. 1997 Experimental investigation on the effect of eccentricity on Taylor–Couette flow. In Transport Phenomena in Thermal Science and Process Engineering, pp. 685–689. Kyoto, Japan.Google Scholar
Younes, M. A. M. A. 1972 The hydrodynamic stability of spiral flow between eccentric rotating cylinders. PhD thesis, University of Leeds.Google Scholar
Younes, M. A. M. A., Mobbs, F. R. & Coney, J. E. R. 1972 Hydrodynamic stability of the flow between eccentric rotating cylinders with axial flow: torque measurements (paper C76/72). In Tribology Convention, Institution of Mechanical Engineers, pp. 14–19.Google Scholar