Article contents
Temperature statistics above a deep-ocean sloping boundary
Published online by Cambridge University Press: 25 June 2015
Abstract
We present a detailed analysis of temperature statistics in an oceanographic observational dataset. The data are collected using a moored array of thermistors, 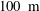 $100~\text{m}$ tall and starting
$100~\text{m}$ tall and starting 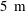 $5~\text{m}$ above the bottom, deployed during four months above the slopes of a Seamount in the north-eastern Atlantic Ocean. Turbulence at this location is strongly affected by the semidiurnal tidal wave. Mean stratification is stable in the entire dataset. We compute structure functions, of order up to 10, of the distributions of temperature increments. Strong intermittency is observed, in particular, during the downslope phase of the tide, and farther from the solid bottom. In the lower half of the mooring during the upslope phase, the temperature statistics are consistent with those of a passive scalar. In the upper half of the mooring, the temperature statistics deviate from those of a passive scalar, and evidence of turbulent convective activity is found. The downslope phase is generally thought to be more shear-dominated, but our results suggest on the other hand that convective activity is present. High-order moments also show that the turbulence scaling behaviour breaks at a well-defined scale (of the order of the buoyancy length scale), which is however dependent on the flow state (tidal phase, height above the bottom). At larger scales, wave motions are dominant. We suggest that our results could provide an important reference for laboratory and numerical studies of mixing in geophysical flows.
$5~\text{m}$ above the bottom, deployed during four months above the slopes of a Seamount in the north-eastern Atlantic Ocean. Turbulence at this location is strongly affected by the semidiurnal tidal wave. Mean stratification is stable in the entire dataset. We compute structure functions, of order up to 10, of the distributions of temperature increments. Strong intermittency is observed, in particular, during the downslope phase of the tide, and farther from the solid bottom. In the lower half of the mooring during the upslope phase, the temperature statistics are consistent with those of a passive scalar. In the upper half of the mooring, the temperature statistics deviate from those of a passive scalar, and evidence of turbulent convective activity is found. The downslope phase is generally thought to be more shear-dominated, but our results suggest on the other hand that convective activity is present. High-order moments also show that the turbulence scaling behaviour breaks at a well-defined scale (of the order of the buoyancy length scale), which is however dependent on the flow state (tidal phase, height above the bottom). At larger scales, wave motions are dominant. We suggest that our results could provide an important reference for laboratory and numerical studies of mixing in geophysical flows.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 15
- Cited by



