Published online by Cambridge University Press: 24 November 2023
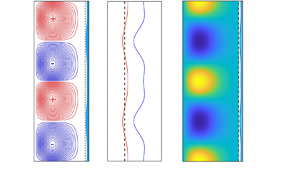
A linear stability analysis of circular Couette flow of a Bingham fluid subjected to axisymmetric perturbations was presented by Peng & Zhu (J. Fluid Mech., vol. 512, 2004, pp. 21–45) and Landry et al. (J. Fluid Mech., vol. 560, 2006, pp. 321–353). Here, we consider the stability of this flow with respect to a finite amplitude perturbation. We focus particularly on the case where the basic flow has an unyielded fluid layer on outer cylinder. A weakly nonlinear stability analysis is developed for a wide gap and a narrow gap. A third-order Ginzburg–Landau equation is derived, and the influence of the different nonlinearities on bifurcation features is investigated in detail. The results indicate that: (i) the nonlinear inertial terms act in favour of pitchfork supercritical bifurcation and the nonlinear yield stress terms promote a subcritical bifurcation; (ii) for a range of Bingham numbers  $B$, the extent of which depends on the radius ratio and outer Reynolds number, the nonlinear yield stress terms are dominant and the primary bifurcation is subcritical. The amplitude analysis indicates that in the supercritical bifurcation regime, near the threshold, when the nonlinear inertial terms are dominant, the amplitude decreases slightly with increasing
$B$, the extent of which depends on the radius ratio and outer Reynolds number, the nonlinear yield stress terms are dominant and the primary bifurcation is subcritical. The amplitude analysis indicates that in the supercritical bifurcation regime, near the threshold, when the nonlinear inertial terms are dominant, the amplitude decreases slightly with increasing  $B$. Once the nonlinear yield stress terms start to become significant, the equilibrium amplitude increases substantially with increasing
$B$. Once the nonlinear yield stress terms start to become significant, the equilibrium amplitude increases substantially with increasing  $B$. Similar trends are observed for Taylor vortex strength. Finally, the erosion of the static layer is analysed. It is shown that the nonlinear yield stress terms play a significant role.
$B$. Similar trends are observed for Taylor vortex strength. Finally, the erosion of the static layer is analysed. It is shown that the nonlinear yield stress terms play a significant role.