Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-04T19:34:20.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Tayler instability in liquid metal columns and liquid metal batteries

Published online by Cambridge University Press:  15 April 2015

W. Herreman ,
C. Nore ,
L. Cappanera  and
J.-L. Guermond
W. Herreman*
Affiliation:
Laboratoire d’Informatique pour la Mécanique et les Sciences de l’Ingénieur, CNRS UPR 3251, BP 133, 91403 Orsay CEDEX and Université Paris-Sud 11, France
C. Nore
Affiliation:
Laboratoire d’Informatique pour la Mécanique et les Sciences de l’Ingénieur, CNRS UPR 3251, BP 133, 91403 Orsay CEDEX and Université Paris-Sud 11, France
L. Cappanera
Affiliation:
Laboratoire d’Informatique pour la Mécanique et les Sciences de l’Ingénieur, CNRS UPR 3251, BP 133, 91403 Orsay CEDEX and Université Paris-Sud 11, France Department of Mathematics, Texas A&M University, 3368 TAMU, College Station, TX 77843-3368, USA
J.-L. Guermond
Affiliation:
Laboratoire d’Informatique pour la Mécanique et les Sciences de l’Ingénieur, CNRS UPR 3251, BP 133, 91403 Orsay CEDEX and Université Paris-Sud 11, France Department of Mathematics, Texas A&M University, 3368 TAMU, College Station, TX 77843-3368, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we investigate the Tayler instability in an incompressible, viscous and resistive liquid metal column and in a model of a liquid metal battery (LMB). Detailed comparisons between theory and numerics, both in linear and nonlinear regimes, are performed. We identify the timescale that is well adapted to the quasi-static (QS) regime and find the range of Hartmann numbers where this approximation applies. 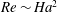The scaling law $\mathit{Re}\sim \mathit{Ha}^{2}$ for the amplitude of the Tayler destabilized flow is explained using a weakly nonlinear argument. We calculate a critical electrolyte height above which the Tayler instability is too weak to disrupt the electrolyte layer in a LMB. Applied to present day Mg-based batteries, this criterion shows that short circuits can occur only in very large batteries. Finally, preliminary results demonstrate the feasibility of direct numerical multiphase simulations of the Tayler instability in a model battery.

JFM classification

MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Multiphase flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 771 , 25 May 2015 , pp. 79 - 114
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agruss, B. 1963 The thermally regenerative liquid-metal cell. J. Electrochem. Soc. 110 (11), 1097–1103.CrossRefGoogle Scholar
Bonanno, A., Brandenburg, A., Del Sordo, F. & Mitra, D. 2012 Breakdown of chiral symmetry during saturation of the Tayler instability. Phys. Rev. E 86 (1), 016313.CrossRefGoogle ScholarPubMed
Bradwell, D. J., Kim, H., Sirk, A. H. C. & Sadoway, D. R. 2012 Magnesium–antimony liquid metal battery for stationary energy storage. J. Am. Chem. Soc. 134 (4), 1895–1897.CrossRefGoogle ScholarPubMed
Cairns, E. J., Crouthamel, C. E., Fischer, A. K., Foster, M. S., Hesson, J. C., Johnson, C. E., Shimotake, H. & Tevebaugh, A. D.1967 Galvanic cells with fused-salt electrolytes. Tech. Rep. Argonne National Lab., IL.CrossRefGoogle Scholar
Cairns, E. J. & Shimotake, H. 1969 High-temperature batteries. Science 164 (3886), 1347–1355.CrossRefGoogle ScholarPubMed
Crawley, A. F. & Kiff, D. R. 1972 The density and viscosity of liquid antimony. Metall. Trans. 3 (1), 157–159.CrossRefGoogle Scholar
Crouthamel, C. E. & Recht, H. L.1967 Regenerative EMF cells: a symposium co-sponsored by the Division of Industrial and Engineering Chemistry and the Division of Fuel Chemistry at the 149th meeting of the American Chemical Society, Detroit, MI, April 8–9, 1965. American Chemical Society.CrossRefGoogle Scholar
Giesecke, A., Nore, C., Stefani, F., Gerbeth, G., Léorat, J., Herreman, W., Luddens, F. & Guermond, J.-L. 2012 Influence of high-permeability discs in an axisymmetric model of the Cadarache dynamo experiment. New J. Phys. 14 (5), 053005.CrossRefGoogle Scholar
Guermond, J.-L., Laguerre, R., Léorat, J. & Nore, C. 2009 Nonlinear magnetohydrodynamics in axisymmetric heterogeneous domains using a Fourier/finite element technique and an interior penalty method. J. Comput. Phys. 228, 2739–2757.CrossRefGoogle Scholar
Guermond, J.-L., Léorat, J., Luddens, F., Nore, C. & Ribeiro, A. 2011a Effects of discontinuous magnetic permeability on magnetodynamic problems. J. Comput. Phys. 230, 6299–6319.CrossRefGoogle Scholar
Guermond, J.-L., Pasquetti, R. & Popov, B. 2011b Entropy viscosity method for nonlinear conservation laws. J. Comput. Phys. 230 (11), 4248–4267.CrossRefGoogle Scholar
Kelley, D. H. & Sadoway, D. R. 2014 Mixing in a liquid metal electrode. Phys. Fluids 26 (5), 057102.CrossRefGoogle Scholar
Kim, H., Boysen, D. A., Newhouse, J. M., Spatocco, B. L., Chung, B., Burke, P. J., Bradwell, D. J., Jiang, K., Tomaszowska, A. A., Wang, K., Wei, W., Ortiz, L. A., Barriga, S. A., Poizeau, S. M. & Sadoway, D. R. 2013 Liquid metal batteries: past, present, and future. Chem. Rev. 113 (3), 2075–2099.CrossRefGoogle ScholarPubMed
Nore, C., Guermond, J.-L., Laguerre, R., Léorat, J. & Luddens, F. 2012 Nonlinear dynamo in a short Taylor–Couette setup. Phys. Fluids 24 (9), 094106, 1–15.CrossRefGoogle Scholar
Nore, C., Léorat, J., Guermond, J.-L. & Luddens, F. 2011 Nonlinear dynamo action in a precessing cylindrical container. Phys. Rev. E 84, 016317.CrossRefGoogle Scholar
Rüdiger, G., Gellert, M., Schultz, M., Strassmeier, K. G., Stefani, F., Gundrum, T., Seilmayer, M. & Gerbeth, G. 2012 Critical fields and growth rates of the Tayler instability as probed by a columnar gallium experiment. Astrophys. J. 755 (2), 181.CrossRefGoogle Scholar
Rüdiger, G. & Schultz, M. 2010 Tayler instability of toroidal magnetic fields in MHD Taylor–Couette flows. Astron. Nachr. 331 (1), 121–129.CrossRefGoogle Scholar
Rüdiger, G., Schultz, M. & Gellert, M. 2011 The Tayler instability of toroidal magnetic fields in a columnar gallium experiment. Astron. Nachr. 332 (1), 17–23.CrossRefGoogle Scholar
Seilmayer, M., Stefani, F., Gundrum, T., Weier, T., Gerbeth, G., Gellert, M. & Rüdiger, G. 2012 Experimental evidence for a transient Tayler instability in a cylindrical liquid–metal column. Phys. Rev. Lett. 108, 244501.CrossRefGoogle Scholar
Sohal, M. S., Ebner, M. A., Sabharwall, P. & Sharpe, P.2013 Engineering Database of Liquid Salt Thermophysical and Thermochemical Properties. Available at: http://www5vip.inl.gov/technicalpublications/Documents/4502650.pdf.Google Scholar
Stefani, F., Weier, T., Gundrum, Th. & Gerbeth, G. 2011 How to circumvent the size limitation of liquid metal batteries due to the Tayler instability. Energy Convers. Manage. 52, 2982–2986.CrossRefGoogle Scholar
Steunenberg, R. K. & Burris, L.2000 From test tube to pilot plant, a 50 year history of the chemical technology division at argonne national laboratory. Tech. Rep. Argonne National Lab., IL (US).CrossRefGoogle Scholar
Swinkels, D. A. J. 1971 Molten salt batteries and fuel cells. In Advances in Molten Salt Chemistry (ed. Braunstein, J., Mamantov, G. & Smith, G. P.), pp. 165–223. Springer.CrossRefGoogle Scholar
Tayler, R. J. 1957 Hydromagnetic instabilities of an ideally conducting fluid. Proc. R. Soc. B 70 (1), 31–48.Google Scholar
Tayler, R. J. 1960 Stability of twisted magnetic fields in a fluid of finite electrical conductivity. Rev. Mod. Phys. 32, 907–913.CrossRefGoogle Scholar
Tayler, R. J. 1973 The adiabatic stability of stars containing magnetic fields – I. Mon. Not. R. Astron. Soc. 161, 365–380.CrossRefGoogle Scholar
Vandakurov, Y. V. 1972 Theory for the stability of a star with a toroidal magnetic field. Sov. Astron. 16 (2), 265–272.Google Scholar
Wang, K., Jiang, K., Chung, B., Ouchi, T., Burke, P. J., Boysen, D. A., Bradwell, D. J., Kim, H., Muecke, U. & Sadoway, D. R. 2014 Lithium–antimony–lead liquid metal battery for grid-level energy storage. Nature 514 (7522), 348–350.CrossRefGoogle ScholarPubMed
Weaver, R. D., Smith, S. W. & Willmann, N. L. 1962 The sodium tin liquid-metal cell. J. Electrochem. Soc. 109 (8), 653–657.CrossRefGoogle Scholar
Weber, N., Galindo, V., Stefani, F. & Weier, T. 2014 Current-driven flow instabilities in large-scale liquid metal batteries, and how to tame them. J. Power Sour. 265, 166–173.CrossRefGoogle Scholar
Weber, N., Galindo, V., Stefani, F., Weier, T. & Wondrak, T. 2013 Numerical simulation of the Tayler instability in liquid metals. New J. Phys. 15 (4), 043034.CrossRefGoogle Scholar