Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T12:32:41.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Systematic errors of skin-friction measurements by oil-film interferometry

Published online by Cambridge University Press:  21 May 2015

Antonio Segalini ,
Jean-Daniel Rüedi  and
Peter A. Monkewitz
Antonio Segalini*
Affiliation:
Linné FLOW Centre, KTH Mechanics, S-100 44, Stockholm, Sweden Department of Industrial Engineering, DIN, University of Bologna, 47100 Forlí, Italy
Jean-Daniel Rüedi
Affiliation:
Department of Industrial Engineering, DIN, University of Bologna, 47100 Forlí, Italy
Peter A. Monkewitz
Affiliation:
Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015, Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In recent years, the independent measurement of wall shear stress with oil-film or oil-drop interferometry has become a cornerstone of turbulent-boundary-layer research as many arguments depend critically on a precise knowledge of the skin friction 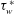${\it\tau}_{w}^{\ast }$. To our knowledge, all practitioners of oil-drop interferometry have so far used the leading-order similarity solution for asymptotically thin, wedge-shaped, two-dimensional oil films established by Tanner & Blows (J. Phys. E: Sci. Instrum., vol. 9, 1976, pp. 194–202) to relate the evolution of drop thickness to 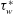${\it\tau}_{w}^{\ast }$. It is generally believed that this procedure, if carefully implemented, yields the true time-averaged 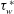${\it\tau}_{w}^{\ast }$ within 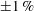$\pm 1\,\%$ or possibly better, but the systematic errors due to the finite thickness of the oil film have never been determined. They are analysed here for oil films with a thickness of the order of a viscous unit in a zero-pressure-gradient turbulent boundary layer. Neglecting spanwise surface curvature and surface tension effects, corrections due to the secondary air boundary layer above the oil film are derived with a linearised triple-layer approach that accounts for the turbulent shear-stress perturbation by means of modified van-Driest-type closure models. In addition, the correction due to processing oil drops with a slight streamwise surface curvature as if they were exact wedges is quantified. Both corrections are evaluated for oil-drop interferograms acquired in a zero-pressure-gradient turbulent boundary layer at a Reynolds number of around 3500, based on displacement thickness, and are shown to produce a reduction of the friction velocity relative to the basic Tanner and Blows theory of between 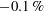$-0.1\,\%$ and 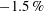$-1.5\,\%$, depending on the mixing-length model. Despite the uncertainty about the true correction, the analysis allows the formulation of some guidelines on where and when to analyse interference fringes in order to minimise the error on the measured wall shear stress.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 773 , 25 June 2015 , pp. 298 - 326
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions. US National Bureau of Standards.Google Scholar
Alfredsson, P. H., Imayama, S., Lingwood, R. J., Örlü, R. & Segalini, A. 2013 Turbulent boundary layers over flat plates and rotating disks – The legacy of von Kármán: a Stockholm perspective. Eur. J. Mech. (B/Fluids) 40, 17–29.CrossRefGoogle Scholar
Bailey, S. C. C., Hultmark, M., Monty, J. P., Alfredsson, P. H., Chong, M. S., Duncan, R. D., Fransson, J. H. M., Hutchins, N., Marusic, I., McKeon, B. J., Nagib, H. M., Örlü, R., Segalini, A., Smits, A. J. & Vinuesa, R. 2013 Obtaining accurate mean velocity measurements in high Reynolds number turbulent boundary layers using Pitot tubes. J. Fluid Mech. 715, 642–670.CrossRefGoogle Scholar
Brown, J. L. & Naughton, J. W.1999 The thin oil film equation. NASA Tech. Mem. 208767.Google Scholar
Bruns, J. M.1998 Experimental investigation of a three-dimensional turbulent boundary layer in an ‘S’-shaped duct. PhD thesis, Technical University Berlin.CrossRefGoogle Scholar
Bruns, J. M., Fernholz, H. H. & Monkewitz, P. A. 1999 An experimental investigation of a three-dimensional turbulent boundary layer in an ‘S’-shaped duct. J. Fluid Mech. 393, 175–213.CrossRefGoogle Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.CrossRefGoogle Scholar
van Driest, E. R. 1956 On turbulent flow near a wall. J. Aeronaut. Sci. 23, 1007–1011.CrossRefGoogle Scholar
Fernholz, H. H., Janke, G., Schober, M., Wagner, P. M. & Warnack, D. 1996 New developments and applications of skin-friction measuring techniques. Meas. Sci. Technol. 7, 1396–1409.CrossRefGoogle Scholar
Jackson, P. S. & Hunt, J. C. R. 1975 Turbulent wind flow over a low hill. Q. J. R. Meteorol. Soc. 101, 929–955.CrossRefGoogle Scholar
Janke, G.1993 Über die grundlagen und einige anwendungen der ölfilm-interferometrie zur messung von wandreibungsfeldern in luftströmungen. PhD thesis, Technische Universität Berlin.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows: recent advances and key issues. Phys. Fluids 22, 065103.CrossRefGoogle Scholar
Mellor, G. L. 1972 The large Reynolds number, asymptotic theory of turbulent boundary layers. Intl J. Engng Sci. 10, 851–873.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-consistent high-Reynolds number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20, 105102.CrossRefGoogle Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variation of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 On the asymptotic state of zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google ScholarPubMed
Nagib, H., Smits, A., Marusic, I. & Alfredsson, P. H.2009 ICET – international collaboration on experiments in turbulence: coordinated measurements in high Reynolds number turbulent boundary layers from three wind tunnels. In APS Bulletin of the 62nd Annual Meeting of the APS Division of Fluid Dynamics, Minneapolis.Google Scholar
Österlund, J. M.1999 Experimental studies of zero pressure-gradient turbulent boundary layer flow. PhD thesis, Kungliga Tekniska Högskolan (Royal Institute of Technology), Stockholm.Google Scholar
Rüedi, J.-D., Duncan, R., Imayama, S. & Chauhan, K.2009 Accurate and independent measurements of wall-shear stress in turbulent flows. In APS Bulletin of the 62nd Annual Meeting of the APS Division of Fluid Dynamics, Minneapolis.Google Scholar
Rüedi, J.-D., Nagib, H. M., Österlund, J. & Monkewitz, P. A. 2003 Evaluation of three techniques for wall-shear measurements in three-dimensional flows. Exp. Fluids 35, 389–396.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Stewartson, K. & Williams, P. G. 1969 Self-induced separation. Proc. R. Soc. Lond. A 312, 181–206.Google Scholar
Sykes, R. I. 1980 An asymptotic theory of incompressible turbulent boundary-layer flow over a small hump. J. Fluid Mech. 101, 647–670.CrossRefGoogle Scholar
Tanner, L. H. & Blows, L. G. 1976 A study of the motion of oil films on surfaces in air flow, with application to the measurement of skin friction. J. Phys. E: Sci. Instrum. 9, 194–202.CrossRefGoogle Scholar
Tanner, L. H. & Kulkarny, V. G. 1976 The viscosity balance method of skin friction measurement: further developments including applications to three-dimensional flow. J. Phys. E: Sci. Instrum. 9, 1114–1121.CrossRefGoogle Scholar
Vinuesa, R., Bartrons, E., Chiu, D., Dressler, K. M., Rüedi, J.-D., Suzuki, Y. & Nagib, H. M. 2014 New insight into flow development and two dimensionality of turbulent channel flows. Exp. Fluids 55, 1759.CrossRefGoogle Scholar