Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-04T21:06:57.148Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetry breaking and instabilities of conical vortex pairs over slender delta wings

Published online by Cambridge University Press:  26 October 2017

Bao-Feng Ma ,
Zhijin Wang  and
Ismet Gursul Open the ORCID record for Ismet Gursul [Opens in a new window]
Bao-Feng Ma
Affiliation:
Ministry of Education Key Laboratory of Fluid Mechanics, Beihang University, Beijing 100191, China
Zhijin Wang
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
Ismet Gursul*
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

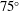An investigation of symmetry breaking and naturally occurring instabilities over thin slender delta wings with sharp leading edges was carried out in a water tunnel using particle image velocimetry (PIV) measurements. Time-averaged location, strength and core radius of conical vortices vary almost linearly with chordwise distance for three delta wings with $75^{\circ }$, 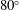$80^{\circ }$ and 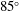$85^{\circ }$ sweep angles over a wide range of angles of attack. Properties of the time-averaged vortex pairs depend only on the similarity parameter, which is a function of the angle of attack and the sweep angle. It is shown that time-averaged vortex pairs develop asymmetry gradually with increasing values of the similarity parameter. Vortex asymmetry can develop in the absence of vortex breakdown on the wing. Instantaneous PIV snapshots were analysed using proper orthogonal decomposition and dynamic mode decomposition, revealing the shear layer and vortex instabilities. The shear layer mode is the most periodic and more dominant for lower values of the similarity parameter. The Strouhal number based on the free stream velocity component in the cross-flow plane is a function of only the similarity parameter. The dominant frequency of the shear layer mode decreases with the increasing similarity parameter. The vortex modes reveal the fluctuations of the vorticity magnitude and helical displacement of the cores, but with little periodicity. There is little correlation between the fluctuations in the cores of the vortices.

JFM classification

Aerodynamics: Aerodynamics Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 41 - 72
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16, 1–4.Google Scholar
Ayoub, A. & McLachlan, B. G 1987 Slender delta wing at high angles of attack – a flow visualization study. In AIAA 19th Fluid Dynamics, Plasma Dynamics and Lasers Conference, June 8–10, Honolulu, Hawaii, AIAA Paper 87-1230, American Institute of Aeronautics and Astronautics.Google Scholar
Birds, J. D.1969 Tuft-grid surveys at low speeds for delta wings. NASA Technical Note 5045.Google Scholar
Brown, C. E. & Michael, W. H. 1954 Effect of leading-edge separation on the lift of a delta wing. J. Aerosp. Sci. 21, 690–694.Google Scholar
Bulathsinghala, D., Jackson, R., Wang, Z. & Gursul, I. 2017 Afterbody vortices of axisymmetric cylinders with a slanted base. Exp. Fluids 58, 60;doi:10.1007/s00348-017-2343-9.Google Scholar
Cai, J., Liu, F. & Luo, S.2001 Stability of symmetric vortices over slender conical bodies at high angles of attack. AIAA Paper 2001-2845.Google Scholar
Cai, J., Liu, F. & Luo, S. 2003 Stability of symmetric vortices in two dimensions and over three-dimensional slender conical bodies. J. Fluid Mech. 480, 65–94.CrossRefGoogle Scholar
Cerretelli, C. & Williamson, C. H. K. 2003 The physical mechanism for vortex merging. J. Fluid Mech. 475, 41–77.Google Scholar
Chen, C., Wang, Z., Cleaver, D. J. & Gursul, I.2016 Interaction of trailing vortices with downstream wings. AIAA Paper 2016-1848.Google Scholar
Cipolla, K. M. & Rockwell, D. 1998 Small-scale vortical structures in crossflow plane of a rolling delta wing. AIAA J. 36, 2276–2278.Google Scholar
Degani, D. 1991 Effect of geometrical disturbances on vortex asymmetry. AIAA J. 29, 560–566.Google Scholar
Degani, D. & Tobak, M. 1992 Experimental study of controlled tip disturbance effect on flow asymmetry. Phys. Fluids. 4, 2825–2832.Google Scholar
Del Pino, C., Lopez-Alonso, J. M., Parras, L. & Fernandez-Feria, R. 2011 Dynamics of the wing-tip vortex in the near field of a NACA0012 aerofoil. Aeronaut. J. 111, 229–239.CrossRefGoogle Scholar
Delery, J. M. 1994 Aspects of vortex breakdown. Prog. Aerosp. Sci. 30, 1–59.Google Scholar
Devenport, W. J., Rife, M. C., Liapis, S. I. & Follin, G. J. 1996 The structure and development of a wing-tip vortex. J. Fluid Mech. 312, 67–106.Google Scholar
Edstrand, A. M., Davis, T. B., Schmid, P. J., Taira, K. & Cattafesta, L. N. 2016 On the mechanism of trailing vortex wandering. J. Fluid Mech. 801, R1-1–R1-11.Google Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
Gad-el-Hak, M. & Blackwelder, R. F. 1985 The discrete vortices from a delta wing. AIAA J. 23, 961–962.Google Scholar
Gordnier, R. & Visbal, M. R. 1994 Unsteady vortex structure over a delta wing. J. Aircraft 31, 243–248.Google Scholar
Gursul, I. 1994 Unsteady flow phenomena over delta wings at high angle of attack. AIAA J. 32, 225–231.Google Scholar
Gursul, I. 2005 Review of unsteady vortex flows over slender delta wings. J. Aircraft 42, 299–319.CrossRefGoogle Scholar
Gursul, I. & Yang, H. 1995 On fluctuations of vortex breakdown location. Phys. Fluids 7, 229–231.Google Scholar
Hall, M. G. 1961 A theory for the core of a leading-edge vortex. J. Fluid Mech. 11, 209–228.Google Scholar
Heaton, C. J. & Peake, N. 2007 Transient growth in vortices with axial flow. J. Fluid Mech. 587, 271–301.Google Scholar
Heiland, R. W.1992 KLTOOL: a mathematical tool for analyzing spatiotemporal data, Master thesis, Arizona State University, Dept of Mathematics.Google Scholar
Huang, M. K. & Chow, C. Y. 1996 Stability of leading-edge vortex pair on a slender delta wing. AIAA J. 34, 1182–1187.Google Scholar
Keener, E. R. & Chapman, G. T. 1977 Similarity in vortex asymmetries over slender bodies and wings. AIAA J. 15, 1370–1372.Google Scholar
Lee, M. & Ho, C.-M. 1990 Lift force of delta wings. Appl. Mech. Rev. 43, 209–221.Google Scholar
Leibovich, S. 1984 Vortex stability and breakdown – survey and extension. AIAA J. 22, 1192–1206.Google Scholar
Leweke, T., Le Dizés, S. & Williamson, C. H. K. 2016 Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 48, 507–541.CrossRefGoogle Scholar
Lim, T. T., Lua, K. B. & Luo, S. C. 2001 Role of tip and edge geometry on vortex asymmetry. AIAA J. 39, 539–543.Google Scholar
Lowson, M. V. & Ponton, A. J. C. 1992 Symmetry breaking in vortex flows on conical bodies. AIAA J. 30, 1576–1583.Google Scholar
Lumley, J. L. 1970 Stochastic tools in turbulence. Applied Mathematics and Mechanics, vol. 12. Academic.Google Scholar
Menke, M. & Gursul, I. 1997 Unsteady nature of leading edge vortices. Phys. Fluids 9, 1–7.Google Scholar
Menke, M., Yang, H. & Gursul, I. 1999 Experiments on the unsteady nature of vortex breakdown over delta wings. Exp. Fluids 27, 262–272.Google Scholar
Polhamus, E. C. 1971 Predictions of vortex-lift characteristics by a leading-edge suction analogy. J. Aircraft 8, 193–199.Google Scholar
Pradeep, D. S. & Hussain, F. 2006 Transient growth of perturbations in a vortex column. J. Fluid Mech. 550, 251–288.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry – A Practical Guide, 2nd edn. Springer.Google Scholar
Renac, F. & Jacquin, L. 2007 Linear stability properties of lifting vortices over delta wings. AIAA J. 45, 1942–1951.Google Scholar
Roy, C. & Leweke, T.2008 Experiments on vortex meandering. FARWake Technical Report AST4-CT-2005-012238, CNRS-IRPHE, also presented in International Workshop on Fundamental Issues Related to Aircraft Trailing Wakes 27–29 May 2008, Marseille, France.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Parts I–III. Q. Appl. Maths 45, 561–590.Google Scholar
Smith, J. H. B. 1968 Improved calculations of leading-edge separation from slender, thin, delta wings. Proc. R. Soc. Lond. A 306, 67–90.Google Scholar
Stahl, W. H., Mahmood, M. & Asghar, A. 1992 Experimental investigations of the vortex flow on delta wings at high incidence. AIAA J. 30, 1027–1032.Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar
Towfighi, J. & Rockwell, D. 1993 Instantaneous structure of vortex breakdown on a pitching delta wing. AIAA J. 31, 1160–1162.Google Scholar
Tobak, M. & Peake, D. J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14, 61–85.CrossRefGoogle Scholar
Tu, J. H., Rowley, C. W., Luchtenburg, M., Brunton, S. L. & Kutz, J. N. 2014 On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1, 391–421.Google Scholar
Wang, Z. & Gursul, I. 2012 Unsteady characteristics of inlet vortices. Exp. Fluids 53, 1015–1032.Google Scholar
Wu, G. X., Deng, X. Y. & Wang, Y. K. 2014 Effects of tip perturbation on asymmetric vortex flow over slender delta wings. AIAA J. 52, 886–890.Google Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2006 Vorticity and Vortex Dynamics. p. 73. Springer.Google Scholar
Zhang, X., Wang, Z. & Gursul, I. 2016 Interaction of multiple vortices over a double delta wing. Aerosp. Sci. Technol. 48, 291–307.Google Scholar