Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T11:27:19.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Swirling flow states of compressible single-phase supercritical fluids in a rotating finite-length straight circular pipe

Published online by Cambridge University Press:  21 June 2018

Nguyen Ly ,
Zvi Rusak Open the ORCID record for Zvi Rusak [Opens in a new window]  and
Shixiao Wang Open the ORCID record for Shixiao Wang [Opens in a new window]
Nguyen Ly
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
Zvi Rusak*
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
Shixiao Wang
Affiliation:
Department of Mathematics, University of Auckland, Auckland, 1142, New Zealand
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Steady states of inviscid, compressible and axisymmetric swirling flows of a single-phase, inert, thermodynamically supercritical fluid in a rotating, finite-length, straight, long circular pipe are studied. The fluid thermodynamic behaviour is modelled by the van der Waals equation of state. A nonlinear partial differential equation for the solution of the flow streamfunction is derived from the fluid equations of motion in terms of the inlet flow specific total enthalpy, specific entropy and circulation functions. This equation reflects the complicated, nonlinear thermo-physical interactions in the flows, specifically when the inlet state temperature and density profiles vary around the critical thermodynamic point, flow compressibility is significant and the inlet swirl ratio is high. Several types of solutions of the resulting nonlinear ordinary differential equation for the axially independent case describe the flow outlet state when the pipe is sufficiently long. The approach is applied to an inlet flow described by a solid-body rotation with uniform profiles of the axial velocity and temperature. The solutions are used to form the bifurcation diagrams of steady compressible flows of real fluids as the inlet swirl level and the centreline inlet density are increased at a fixed inlet Mach number and temperature. Focus is on heavy-molecule fluids with low values of 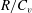$R/C_{v}$. Computed results provide theoretical predictions of the critical swirl levels for the exchange of stability of the columnar state and for the appearance of non-columnar states and of vortex breakdown states as a function of inlet centreline density. The difference in the dynamical behaviour between that of a calorically perfect gas and of a real gas is explored. The analysis sheds new fundamental light on the complex dynamics of high-Reynolds-number, compressible, subsonic swirling flows of real gases.

JFM classification

Compressible Flows: Compressible Flows Vortex Flows: Vortex breakdown Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 576 - 614
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Althaus, W., Brücker, Ch. & Weimer, M. 1995 Breakdown of slender vortices. In Fluid Vortices, pp. 373–426. Springer.Google Scholar
Bazarov, V., Yang, V. & Puneesh, P. 2004 Design and dynamics of jet and swirl injectors. Prog. Astronaut. Aeronaut. 200, 19–103.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14 (4), 593–629.Google Scholar
Beran, P. S. 1994 The time-asymptotic behavior of vortex breakdown in tubes. Comput. Fluids 23 (7), 913–937.Google Scholar
Beran, P. S. & Culick, F. E. C. 1992 The role of non uniqueness in the development of vortex breakdown in tubes. J. Fluid Mech. 242, 491–527.Google Scholar
Brown, G. L. & Lopez, J. M. 1990 Axisymmetric vortex breakdown. Part 2. Physical mechanisms. J. Fluid Mech. 221, 553–576.Google Scholar
Buntine, J. D. & Saffman, P. G. 1995 Inviscid swirling flows and vortex breakdown. Proc. R. Soc. Lond. A 449, 139–153.Google Scholar
Cramer, M. S. 1989 Negative nonlinearity in selected fluorocarbons. Phys. Fluids A 1 (11), 1894–1897.Google Scholar
Cramer, M. S. & Tarkenton, G. M. 1992 Transonic flows of Bethe–Zel’dovich–Thompson fluids. J. Fluid Mech. 240, 197–228.Google Scholar
Crook, L., Rachedi, R. & Sojka, P. 2007 Development of a real-fuel supercritical injection facility. In 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA Paper 2007-5683.Google Scholar
Escudier, M. 1988 Vortex breakdown: observations and explanations. Prog. Aerosp. Sci. 25 (2), 189–229.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4 (1), 195–218.Google Scholar
Herrada, M. A., Prez-Sabroid, M. & Barrero, A. 2003 Vortex breakdown in compressible flows in pipes. Phys. Fluids 15 (8), 2208–2218.Google Scholar
Keller, J. J., Egli, W. & Exley, W. 1985 Force- and loss-free transitions between flow states. Z. Angew. Math. Phys. 36 (6), 854–889.Google Scholar
Kuruvila, G. & Salas, M.1990 Three-dimensional simulation of vortex breakdown. NASA TM 102664.Google Scholar
Lefebvre, A. H. 1989 Atomization and Sprays, Combustion: An International Series. Hemisphere.Google Scholar
Leibovich, S. 1984 Vortex stability and breakdown: survey and extension. AIAA J. 22 (9), 1192–1206.Google Scholar
Leibovich, S. & Kribus, A. 1990 Large-amplitude wavetrains and solitary waves in vortices. J. Fluid Mech. 216, 459–504.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.Google Scholar
Long, R. R. 1953 Steady motion around a symmetrical obstacle moving along the axis of a rotating liquid. J. Met. 10 (3), 197–203.Google Scholar
Lopez, J. M. 1994 On the bifurcation structure of axisymmetric vortex breakdown in a constricted pipe. Phys. Fluids 6 (11), 3683–3693.Google Scholar
Luginsland, T. & Kleiser, L. 2015 Mach number influence on vortex breakdown in compressible, subsonic swirling nozzle-jet flows. In Direct and Large-Eddy Simulation IX, ERCOFTAC Series, vol. 20, pp. 311–317. Springer.Google Scholar
Malkiel, E., Cohen, J., Rusak, Z. & Wang, S. 1996 Axisymmetric vortex breakdown in a pipe: theoretical and experimental studies. In Proceedings of the 36th Israel Annual Conference on Aerospace Sciences, (February), pp. 24–34. Technion.Google Scholar
Mattner, T. W., Joubert, P. N. & Chong, M. S. 2002 Vortical flow. Part 1. Flow through a constant-diameter pipe. J. Fluid Mech. 463, 259–291.Google Scholar
Maxwell, J. C. 1875 On the dynamical evidence of the molecular constitution of bodies. Nature 11, 357–359.Google Scholar
Melville, R.1996 The role of compressibility in free vortex breakdown. AIAA Paper 96-2075.Google Scholar
Mitchell, A. M. & Delery, J. 2001 Research into vortex breakdown control. Prog. Aerosp. Sci. 37 (4), 385–418.Google Scholar
Moran, M. J. & Shapiro, H. N. 1992 Fundamentals of Engineering Thermodynamics, 3rd edn. John Wiley & Sons.Google Scholar
Novak, F. & Sarpkaya, T. 2000 Turbulent vortex breakdown at high Reynolds numbers. AIAA J. 38 (5), 825–834.Google Scholar
Rachedi, R. R., Crook, L. C. & Sojka, P. E. 2010 An experimental study of swirling supercritical Hydrocarbon fuel jets. J. Engng Gas Turbines Power 132 (8), 081502.Google Scholar
Randall, J. D. & Leibovich, S. 1973 The critical state: a trapped wave model of vortex breakdown. J. Fluid Mech. 58 (3), 495–515.Google Scholar
Renac, F., Sipp, D. & Jacquin, L. 2007 Criticality of compressible rotating flows. Phys. Fluids 19 (1), 018101.Google Scholar
Rusak, Z.2000 Review of recent studies on the axisymmetric vortex breakdown phenomenon. In AIAA Fluids 2000 Conference, AIAA Paper 2000-2529.Google Scholar
Rusak, Z., Choi, J. J. & Lee, J.-H. 2007 Bifurcation and stability of near-critical compressible compressible swirling flows. Phys. Fluids 19 (11), 114107.Google Scholar
Rusak, Z., Choi, J. J., Bourquard, N. & Wang, S. 2015a Vortex breakdown of compressible subsonic swirling flows in a finite-length straight circular pipe. J. Fluid Mech. 781, 3–27.Google Scholar
Rusak, Z., Granata, J. & Wang, S. 2015b An active feedback flow control theory of the axisymmetric vortex breakdown process. J. Fluid Mech. 774, 488–528.Google Scholar
Rusak, Z. & Lamb, D. 1999 Prediction of vortex breakdown in leading edge vortices above slender delta wings. J. Aircraft 36 (4), 659–667.Google Scholar
Rusak, Z. & Lee, J.-H. 2002 The effect of compressibility on the critical wwirl of vortex flows in a pipe. J. Fluid Mech. 461, 301–319.Google Scholar
Rusak, Z. & Lee, J.-H. 2004 On the stability of a compressible axisymmetric rotating flow in a pipe. J. Fluid Mech. 501, 25–42.Google Scholar
Rusak, Z. & Wang, C. W. 1997 Transonic flow of dense gases around an airfoil with a parabolic nose. J. Fluid Mech. 346, 1–21.Google Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of near-critical swirling flows in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.Google Scholar
Rusak, Z., Whiting, C. & Wang, S. 1998 Axisymmetric breakdown of a Q-vortex in a pipe. AIAA J. 36 (10), 1848–1853.Google Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45 (3), 545–559.Google Scholar
Sarpkaya, T. 1974 Effect of the adverse pressure-gradient on vortex breakdown. AIAA J. 12 (5), 602–607.Google Scholar
Sarpkaya, T. 1995 Turbulent vortex breakdown. Phys. Fluids 7 (10), 2301–2303.Google Scholar
Schnerr, G. H. & Leidner, P. 1993 Real gas effects on the normal shock behavior near curved walls. Phys. Fluids A 5 (11), 2996–3003.Google Scholar
Squire, H. B. 1956 Rotating fluids. In Surveys in Mechanics (ed. Batchelor, G. K. & Davies, R. M.), pp. 139–161. Cambridge University Press.Google Scholar
Thompson, P. A. 1982 Compressible Fluid Dynamics. McGraw-Hill Inc.Google Scholar
Umeh, C. O. U., Rusak, Z. & Gutmark, E. 2012 Vortex breakdown in a swirl-stabilized combustor. J. Propul. Power 28 (5), 1037–1051.Google Scholar
Umeh, C. O. U., Rusak, Z., Gutmark, E., Villalva, R. & Cha, D. J. 2010 Experimental and computational study of nonreacting vortex breakdown in a swirl-stabilized combustor. AIAA J. 48 (11), 2576–2585.Google Scholar
Vanierschot, M. 2017 On the dynamics of the transition to vortex breakdown in axisymmetric inviscid swirling flows. Eur. J. Mech. (B/Fluids) 65, 65–69.Google Scholar
Wang, S. & Rusak, Z. 1996 On the stability of an axisymmetric rotating flow in a pipe. Phys. Fluids 8 (4), 1007–1016.Google Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar
Zong, N. & Yang, V. 2008 Cryogenic fluid dynamics of pressure swirl injectors at supercritical conditions. Phys. Fluids 20 (5), 056103.Google Scholar