Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T04:23:09.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Swimming in potential flow

Published online by Cambridge University Press:  01 December 2022

Alec Glisman Open the ORCID record for Alec Glisman [Opens in a new window]  and
John F. Brady Open the ORCID record for John F. Brady [Opens in a new window]
Alec Glisman
Affiliation:
Division of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125, USA
John F. Brady*
Affiliation:
Division of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

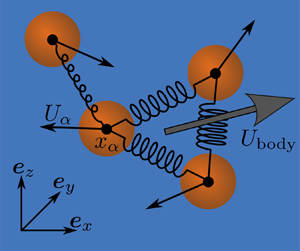
The well-known self-propulsion, or swimming, of a deformable body in Stokes flow (i.e. at low Reynolds number) can be understood and modelled from the variation in the configuration-dependent hydrodynamic resistance tensor throughout the period of deformation. Remarkably, at the other extreme of high Reynolds number, a deformable body may also self-propel without doing any net work on the fluid in potential flow. As a body deforms, the mass of fluid displaced – the so-called added mass – depends on the instantaneous body configuration, and a net displacement is possible over a period of deformation. This potential swimming takes a form identical to that for Stokes swimmers with the configuration-dependent added mass replacing the hydrodynamic resistance tensor. Analytical insight into the swimming of a deformable body is obtained through an expansion of the nonlinear spatial dependence of the hydrodynamic interactions and connections between previous studies of swimming in Stokes flow to those in potential flow are made.

JFM classification

Biological Fluid Dynamics: Propulsion Complex Fluids: Active matter
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , R5
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Avron, J.E., Kenneth, O. & Oaknin, D.H. 2005 Pushmepullyou: an efficient micro-swimmer. New J. Phys. 7 (1), 234.CrossRefGoogle Scholar
Cates, M.E. & Tailleur, J. 2015 Motility-induced phase separation. Annu. Rev. Condens. Matter Phys. 6 (1), 219–244.CrossRefGoogle Scholar
Chambrion, T., Giraldi, L. & Munnier, A. 2019 Optimal strokes for driftless swimmers: a general geometric approach. ESAIM: Control Optim. Calculus Variations 25, 6.Google Scholar
Datt, C. & Elfring, G.J. 2019 Active particles in viscosity gradients. Phys. Rev. Lett. 123 (15), 158006.CrossRefGoogle ScholarPubMed
Dulaney, A.R. & Brady, J.F. 2021 Machine learning for phase behavior in active matter systems. Soft Matt. 17 (28), 6808–6816.CrossRefGoogle ScholarPubMed
Durlofsky, L., Brady, J.F. & Bossis, G. 1987 Dynamic simulation of hydrodynamically interacting particles. J. Fluid Mech. 180, 21–49.CrossRefGoogle Scholar
Golestanian, R. & Ajdari, A. 2008 Analytic results for the three-sphere swimmer at low Reynolds number. Phys. Rev. E 77 (3), 036308.CrossRefGoogle ScholarPubMed
Kanso, E., Marsden, J.E., Rowley, C.W. & Melli-Huber, J.B. 2005 Locomotion of articulated bodies in a perfect fluid. J. Nonlinear Sci. 15 (4), 255–289.CrossRefGoogle Scholar
Klotsa, D. 2019 As above, so below, and also in between: mesoscale active matter in fluids. Soft Matt. 15 (44), 8946–8950.CrossRefGoogle ScholarPubMed
Lamb, H. 1924 Hydrodynamics. University Press.Google Scholar
Lauga, E. & Bartolo, D. 2008 No many-scallop theorem: collective locomotion of reciprocal swimmers. Phys. Rev. E 78 (3), 030901.CrossRefGoogle ScholarPubMed
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.CrossRefGoogle Scholar
Lighthill, M.J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.CrossRefGoogle Scholar
Lighthill, S.J. 1975 Mathematical Biofluiddynamics. SIAM.CrossRefGoogle Scholar
Mallory, S.A., Omar, A.K. & Brady, J.F. 2021 Dynamic overlap concentration scale of active colloids. Phys. Rev. E 104 (4), 044612.CrossRefGoogle ScholarPubMed
Masoud, H. & Stone, H.A. 2019 The reciprocal theorem in fluid dynamics and transport phenomena. J. Fluid Mech. 879, P1.CrossRefGoogle Scholar
Najafi, A. & Golestanian, R. 2004 Simple swimmer at low Reynolds number: three linked spheres. Phys. Rev. E 69 (6), 062901.CrossRefGoogle ScholarPubMed
Pooley, C.M., Alexander, G.P. & Yeomans, J.M. 2007 Hydrodynamic interaction between two swimmers at low Reynolds number. Phys. Rev. Lett. 99 (22), 228103.CrossRefGoogle ScholarPubMed
Purcell, E.M. 1977 Life at low Reynolds number. Am. J. Phys. 45 (1), 3–11.CrossRefGoogle Scholar
Saffman, P.G. 1967 The self-propulsion of a deformable body in a perfect fluid. J. Fluid Mech. 28 (2), 385–389.CrossRefGoogle Scholar
Saffman, P.G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Stone, H.A. & Samuel, A.D.T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77 (19), 4102.CrossRefGoogle ScholarPubMed
Swan, J.W., Brady, J.F., Moore, R.S. & ChE 174 2011 Modeling hydrodynamic self-propulsion with Stokesian dynamics. Or teaching Stokesian dynamics to swim. Phys. Fluids 23 (7), 071901.CrossRefGoogle Scholar
Theers, M., Westphal, E., Qi, K., Winkler, R.G. & Gompper, G. 2018 Clustering of microswimmers: interplay of shape and hydrodynamics. Soft Matt. 14 (42), 8590–8603.CrossRefGoogle ScholarPubMed
Wu, T. 1971 Hydromechanics of swimming propulsion. Part 1. Swimming of a two-dimensional flexible plate at variable forward speeds in an inviscid fluid. J. Fluid Mech. 46 (2), 337–355.CrossRefGoogle Scholar
Wu, T., Brokaw, C.J. & Brennen, C. 1975 Swimming and Flying in Nature. Springer.CrossRefGoogle Scholar
Yurkovetsky, Y. & Brady, J.F. 1996 Statistical mechanics of bubbly liquids. Phys. Fluids 8 (4), 881–895.CrossRefGoogle Scholar