No CrossRef data available.
Published online by Cambridge University Press: 13 September 2024
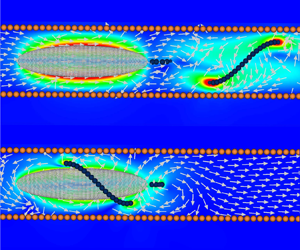
Single-flagellated bacteria are ubiquitous in nature. They exhibit various swimming modes using their flagella to explore complex surroundings such as soil and porous polymer networks. Some single-flagellated bacteria swim with two distinct modes, one with the flagellum extended away from its body and another with the flagellum wrapped around it. The wrapped mode has been observed when bacteria swim under tight confinements or in highly viscous polymeric melts. In this study we investigate the hydrodynamics of these two modes inside a circular pipe. We find that the wrapped mode is slower than the extended mode in bulk but more efficient under strong confinement due to a hydrodynamic increase of its flagellum translation–rotation coupling and an Archimedes’ screw-like configuration that helps to move the fluid along the pipe.