Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T11:26:29.398Z Has data issue: false hasContentIssue false
  • English
  • Français

Suspensions of finite-size neutrally buoyant spheres in turbulent duct flow

Published online by Cambridge University Press:  19 July 2018

Walter Fornari Open the ORCID record for Walter Fornari [Opens in a new window] ,
Hamid Tabaei Kazerooni ,
Jeanette Hussong  and
Luca Brandt Open the ORCID record for Luca Brandt [Opens in a new window]
Walter Fornari*
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-10044 Stockholm, Sweden
Hamid Tabaei Kazerooni
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-10044 Stockholm, Sweden Ruhr-Universität Bochum, Chair of Hydraulic Fluid Machinery, Universitätsstraße 150, 44801 Bochum, Germany
Jeanette Hussong
Affiliation:
Ruhr-Universität Bochum, Chair of Hydraulic Fluid Machinery, Universitätsstraße 150, 44801 Bochum, Germany
Luca Brandt
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-10044 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the turbulent square duct flow of dense suspensions of neutrally buoyant spherical particles. Direct numerical simulations (DNS) are performed in the range of volume fractions 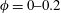$\unicode[STIX]{x1D719}=0{-}0.2$, using the immersed boundary method (IBM) to account for the dispersed phase. Based on the hydraulic diameter a Reynolds number of 5600 is considered. We observe that for 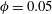$\unicode[STIX]{x1D719}=0.05$ and 0.1, particles preferentially accumulate on the corner bisectors, close to the corners, as also observed for laminar square duct flows of the same duct-to-particle size ratio. At the highest volume fraction, particles preferentially accumulate in the core region. For plane channel flows, in the absence of lateral confinement, particles are found instead to be uniformly distributed across the channel. The intensity of the cross-stream secondary flows increases (with respect to the unladen case) with the volume fraction up to 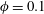$\unicode[STIX]{x1D719}=0.1$, as a consequence of the high concentration of particles along the corner bisector. For 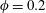$\unicode[STIX]{x1D719}=0.2$ the turbulence activity is reduced and the intensity of the secondary flows reduces to below that of the unladen case. The friction Reynolds number increases with 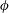$\unicode[STIX]{x1D719}$ in dilute conditions, as observed for channel flows. However, for 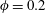$\unicode[STIX]{x1D719}=0.2$ the mean friction Reynolds number is similar to that for 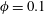$\unicode[STIX]{x1D719}=0.1$. By performing the turbulent kinetic energy budget, we see that the turbulence production is enhanced up to 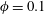$\unicode[STIX]{x1D719}=0.1$, while for 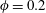$\unicode[STIX]{x1D719}=0.2$ the production decreases below the values for 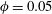$\unicode[STIX]{x1D719}=0.05$. On the other hand, the dissipation and the transport monotonically increase with 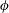$\unicode[STIX]{x1D719}$. The interphase interaction term also contributes positively to the turbulent kinetic energy budget and increases monotonically with 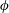$\unicode[STIX]{x1D719}$, in a similar way as the mean transport. Finally, we show that particles move on average faster than the fluid. However, there are regions close to the walls and at the corners where they lag behind it. In particular, for 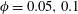$\unicode[STIX]{x1D719}=0.05,0.1$, the slip velocity distribution at the corner bisectors seems correlated to the locations of maximum concentration: the concentration is higher where the slip velocity vanishes. The wall-normal hydrodynamic and collision forces acting on the particles push them away from the corners. The combination of these forces vanishes around the locations of maximum concentration. The total mean forces are generally low along the corner bisectors and at the core, also explaining the concentration distribution for 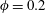$\unicode[STIX]{x1D719}=0.2$.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 148 - 186
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbas, M., Magaud, P., Gao, Y. & Geoffroy, S. 2014 Migration of finite sized particles in a laminar square channel flow from low to high Reynolds numbers. Phys. Fluids 26 (12), 123301.Google Scholar
Amini, H., Sollier, E., Weaver, W. M. & Di Carlo, D. 2012 Intrinsic particle-induced lateral transport in microchannels. Proc. Natl Acad. Sci. USA 109 (29), 11593–11598.Google Scholar
Ardekani, M. N., Costa, P., Breugem, W.-P., Picano, F. & Brandt, L. 2017 Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. J. Fluid Mech. 816, 43–70.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.Google Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.Google Scholar
Breugem, W. P. & Boersma, B. J. 2005 Direct numerical simulations of turbulent flow over a permeable wall using a direct and a continuum approach. Phys. Fluids 17 (2), 025103.Google Scholar
Breugem, W.-P., Van Dijk, V. & Delfos, R. 2014 Flows through real porous media: x-ray computed tomography, experiments, and numerical simulations. J. Fluids Engng 136 (4), 040902.Google Scholar
Chun, B. & Ladd, A. J. C. 2006 Inertial migration of neutrally buoyant particles in a square duct: an investigation of multiple equilibrium positions. Phys. Fluids 18 (3), 031704.Google Scholar
Costa, P., Boersma, B. J., Westerweel, J. & Breugem, W.-P. 2015 Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92 (5), 053012.Google Scholar
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2016 Universal scaling laws for dense particle suspensions in turbulent wall-bounded flows. Phys. Rev. Lett. 117 (13), 134501.Google Scholar
Doyeux, V., Priem, S., Jibuti, L., Farutin, A., Ismail, M. & Peyla, P. 2016 Effective viscosity of two-dimensional suspensions: confinement effects. Phys. Rev. Fluids 1 (4), 043301.Google Scholar
Fornari, W., Brandt, L., Chaudhuri, P., Lopez, C. U., Mitra, D. & Picano, F. 2016a Rheology of confined non-Brownian suspensions. Phys. Rev. Lett. 116 (1), 018301.Google Scholar
Fornari, W., Formenti, A., Picano, F. & Brandt, L. 2016b The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions. Phys. Fluids 28 (3), 033301.Google Scholar
Fornari, W., Picano, F. & Brandt, L. 2016c Sedimentation of finite-size spheres in quiescent and turbulent environments. J. Fluid Mech. 788, 640–669.Google Scholar
Fornari, W., Picano, F. & Brandt, L. 2018 The effect of polydispersity in a turbulent channel flow laden with finite-size particles. Eur. J. Mech. (B/Fluids) 67, 54–64.Google Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.Google Scholar
Gessner, F. B. 1973 The origin of secondary flow in turbulent flow along a corner. J. Fluid Mech. 58 (01), 1–25.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics, vol. 45. Cambridge University Press.Google Scholar
Henningson, D. S. & Kim, J. 1991 On turbulent spots in plane Poiseuille flow. J. Fluid Mech. 228, 183–205.Google Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65 (2), 365–400.Google Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.Google Scholar
Jones, O. C. 1976 An improvement in the calculation of turbulent friction in rectangular ducts. J. Fluids Engng 98 (2), 173–180.Google Scholar
Joung, Y., Choi, S.-U. & Choi, J.-I. 2007 Direct numerical simulation of turbulent flow in a square duct: analysis of secondary flows. J. Engng Mech. 133 (2), 213–221.Google Scholar
Kazerooni, H. T., Fornari, W., Hussong, J. & Brandt, L. 2017 Inertial migration in dilute and semidilute suspensions of rigid particles in laminar square duct flow. Phys. Rev. Fluids 2, 084301.Google Scholar
Koh, C. J., Hookham, P. & Leal, L. G. 1994 An experimental investigation of concentrated suspension flows in a rectangular channel. J. Fluid Mech. 266, 1–32.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277 (1), 109–134.Google Scholar
Kulkarni, P. M. & Morris, J. F. 2008 Suspension properties at finite Reynolds number from simulated shear flow. Phys. Fluids 20, 040602.Google Scholar
Lashgari, I., Ardekani, M. N., Banerjee, I., Russom, A. & Brandt, L. 2017a Inertial migration of spherical and oblate particles in straight ducts. J. Fluid Mech. 819, 540–561.Google Scholar
Lashgari, I., Picano, F. & Brandt, L. 2015 Transition and self-sustained turbulence in dilute suspensions of finite-size particles. Theor. Appl. Mech. Lett. 5 (3), 121–125.Google Scholar
Lashgari, I., Picano, F., Breugem, W.-P. & Brandt, L. 2014 Laminar, turbulent, and inertial shear-thickening regimes in channel flow of neutrally buoyant particle suspensions. Phys. Rev. Lett. 113 (25), 254502.Google Scholar
Lashgari, I., Picano, F., Breugem, W. P. & Brandt, L. 2016 Channel flow of rigid sphere suspensions: particle dynamics in the inertial regime. Intl J. Multiphase Flow 78, 12–24.Google Scholar
Lashgari, I., Picano, F., Costa, P., Breugem, W.-P. & Brandt, L. 2017b Turbulent channel flow of a dense binary mixture of rigid particles. J. Fluid Mech. 818, 623–645.Google Scholar
Lin, Z.-W., Shao, X.-M., Yu, Z.-S. & Wang, L.-P. 2017 Effects of finite-size heavy particles on the turbulent flows in a square duct. J. Hydrodynamics B 29 (2), 272–282.Google Scholar
Liu, C., Xue, C., Sun, J. & Hu, G. 2016 A generalized formula for inertial lift on a sphere in microchannels. Lab on a Chip 16 (5), 884–892.Google Scholar
Loisel, V., Abbas, M., Masbernat, O. & Climent, E. 2013 The effect of neutrally buoyant finite-size particles on channel flows in the laminar-turbulent transition regime. Phys. Fluids 25 (12), 123304.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90 (1), 014501.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, É. 2004 Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.Google Scholar
Maxey, M. 2017 Simulation methods for particulate flows and concentrated suspensions. Annu. Rev. Fluid Mech. 49, 171–193.Google Scholar
Morita, Y., Itano, T. & Sugihara-Seki, M. 2017 Equilibrium radial positions of neutrally buoyant spherical particles over the circular cross-section in Poiseuille flow. J. Fluid Mech. 813, 750–767.Google Scholar
Morris, J. F. 2009 A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 48 (8), 909–923.Google Scholar
Morris, J. F. & Haddadi, H. 2014 Microstructure and rheology of finite inertia neutrally buoyant suspensions. J. Fluid Mech. 749, 431–459.Google Scholar
Nakagawa, N., Yabu, T., Otomo, R., Kase, A., Makino, M., Itano, T. & Sugihara-Seki, M. 2015 Inertial migration of a spherical particle in laminar square channel flows from low to high Reynolds numbers. J. Fluid Mech. 779, 776–793.Google Scholar
Noorani, A., Vinuesa, R., Brandt, L. & Schlatter, P. 2016 Aspect ratio effect on particle transport in turbulent duct flows. Phys. Fluids 28 (11), 115103.Google Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.Google Scholar
Picano, F., Breugem, W.-P., Mitra, D. & Brandt, L. 2013 Shear thickening in non-Brownian suspensions: an excluded volume effect. Phys. Rev. Lett. 111 (9), 098302.Google Scholar
Pinelli, A., Uhlmann, M., Sekimoto, A. & Kawahara, G. 2010 Reynolds number dependence of mean flow structure in square duct turbulence. J. Fluid Mech. 644, 107–122.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pourquie, M. B. J. M., Breugem, W. P. & Boersma, B. J. 2009 Some issues related to the use of immersed boundary methods to represent square obstacles. Intl J. Multiscale Comput. Engng 7 (6), 509–522.Google Scholar
Prandtl, L. 1963 The Essentials of Fluid Dynamics. Blackie & Son Limited.Google Scholar
Reeks, M. W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 14 (6), 729–739.Google Scholar
Roma, A. M., Peskin, C. S. & Berger, M. J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.Google Scholar
Saffman, P. G. T. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.Google Scholar
Samanta, A., Vinuesa, R., Lashgari, I., Schlatter, P. & Brandt, L. 2015 Enhanced secondary motion of the turbulent flow through a porous square duct. J. Fluid Mech. 784, 681–693.Google Scholar
Sardina, G., Picano, F., Schlatter, P., Brandt, L. & Casciola, C. M. 2011 Large scale accumulation patterns of inertial particles in wall-bounded turbulent flow. Flow Turbul. Combust. 86 (3–4), 519–532.Google Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.Google Scholar
Segre, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow part 2. Experimental results and interpretation. J. Fluid Mech. 14 (01), 136–157.Google Scholar
Sharma, G. & Phares, D. J. 2006 Turbulent transport of particles in a straight square duct. Intl J. Multiphase Flow 32 (7), 823–837.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35 (9), 827–839.Google Scholar
Spandan, V., Lohse, D. & Verzicco, R. 2016 Deformation and orientation statistics of neutrally buoyant sub-kolmogorov ellipsoidal droplets in turbulent Taylor–Couette flow. J. Fluid Mech. 809, 480–501.Google Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.Google Scholar
Tanaka, M. 2017 Effect of gravity on the development of homogeneous shear turbulence laden with finite-size particles. J. Turbul. 18 (12), 1144–1179.Google Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.Google Scholar
Vinuesa, R., Noorani, A., Lozano-Durán, A., Khoury, G. K. E., Schlatter, P., Fischer, P. F. & Nagib, H. M. 2014 Aspect ratio effects in turbulent duct flows studied through direct numerical simulation. J. Turbul. 15 (10), 677–706.Google Scholar
Wagner, N. J. & Brady, J. F. 2009 Shear thickening in colloidal dispersions. Phys. Today 62 (10), 27–32.Google Scholar
Winkler, C. M., Rani, S. L. & Vanka, S. P. 2004 Preferential concentration of particles in a fully developed turbulent square duct flow. Intl J. Multiphase Flow 30 (1), 27–50.Google Scholar
Zhao, L. H., Andersson, H. I. & Gillissen, J. J. J. 2010 Turbulence modulation and drag reduction by spherical particles. Phys. Fluids 22 (8), 081702.Google Scholar