Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T20:30:20.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Suspension flow past a cylinder: particle interactions with recirculating wakes

Published online by Cambridge University Press:  10 November 2014

Hamed Haddadi ,
Shahab Shojaei-Zadeh ,
Kevin Connington  and
Jeffrey F. Morris
Hamed Haddadi
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
Shahab Shojaei-Zadeh
Affiliation:
Department of Mechanical and Aerospace Engineering, Rutgers University, 98 Brett Road, Piscataway, NJ 08854, USA
Kevin Connington
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
Jeffrey F. Morris*
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experimental observations of the flow of a suspension of solid fraction 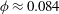${\it\phi}\approx 0.084$ over a circular cylindrical post in a shallow microchannel (depth smaller than the cylinder radius) find that the recirculating wake behind the obstacle at moderate Reynolds numbers is depleted or devoid of particles. Particles injected into the wake exit to regain the depleted state. By numerical simulation of the discrete particle motion, the basis for the depletion behind the cylinder is studied; rather than a shallow channel, the numerical simulations consider a periodic domain, mimicking the flow past an infinite cylinder. The Reynolds number is defined, using the average axial velocity 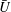${\bar{U}}$, diameter of the obstacle 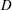$D$ and the kinematic viscosity of the suspension ${\it\nu}$, as 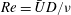$Re={\bar{U}}D/{\it\nu}$, and is studied for 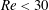$Re<30$ in the simulation – conditions for which the pure fluid exhibits an extended steady closed-streamline (recirculating) wake behind the cylinder; unsteadiness is found to be suppressed by the channel walls in the experiments, allowing steady flow at a larger 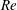$Re$ than expected for an infinite cylinder (up to at least 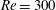$Re=300$). The simulations use the lattice-Boltzmann method to determine the motion of the fluid and neutrally buoyant particles. The trajectory of a single particle (small relative to the cylinder) shows migration to a limit cycle inside the wake. With an increase of the number of particles in the wake alone (no particles in the free stream), particles can escape the wake due to velocity fluctuations. Simulation of the flow of suspensions of 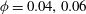${\it\phi}=0.04,0.06$ and 0.08 demonstrates that there is particle exchange between the wake and the free stream; the net flux of particles out of the wake leads to a particle-depleted wake, qualitatively very similar to the experimental observation.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Complex Fluids: Suspensions Wakes/Jets: Wakes/Jets
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 760 , 10 December 2014 , R2
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K., Lu, Y. & Ding, E. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.CrossRefGoogle Scholar
Asmolov, E. S. 1999 The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 381, 63–87.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics, pp. 174–255. Cambridge University Press.Google Scholar
Bearman, P. W. & Zdravkovich, M. M. 1978 Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 89, 33–47.Google Scholar
Burns, T. J., Davis, R. W. & Moore, E. F. 1999 A perturbation study of particle dynamics in a plane wake flow. J. Fluid Mech. 384, 1–26.CrossRefGoogle Scholar
Haddadi, H. & Morris, J. F. 2014 Microstructure and rheology of finite inertia neutrally buoyant suspensions. J. Fluid Mech. 749, 431–459.Google Scholar
Han, H., Kim, C., Kim, M. & Lee, S. 1999 Particle migration in tube flow of suspensions. J. Rheol. 43, 1157–1174.CrossRefGoogle Scholar
Humphry, K. J., Kulkarni, P. M., Weitz, D. A., Morris, J. F. & Stone, H. A. 2010 Axial and lateral particle ordering in finite Reynolds number channel flows. Phys. Fluids 22, 081703.Google Scholar
Kulkarni, P. M. & Morris, J. F. 2008 Suspension properties at finite Reynolds number from simulated shear flow. Phys. Fluids 20, 040602.Google Scholar
Ladd, A. J. C. 1994a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.Google Scholar
Ladd, A. J. C. 1994b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.CrossRefGoogle Scholar
Mach, A. J., Jae, H. K., Arshi, A., Soojung, C. H. & Di Carlo, D. 2011 Automated cellular sample preparation using a centrifuge-on-a-chip. Lab on a Chip 11, 2827–2834.CrossRefGoogle ScholarPubMed
Matas, J. P., Morris, J. F. & Guazzelli, E. 2004 Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid. Mech. 515, 171–195.CrossRefGoogle Scholar
Nguyen, N. Q. & Ladd, A. J. C. 2002 Lubrication corrections for lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E 66, 046708.CrossRefGoogle ScholarPubMed
Segré, G. & Silberberg, A. 1962a Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 1. Determination of local concentration by statistical analysis of particle passages through crossed light beams. J. Fluid Mech. 14, 115–135.Google Scholar
Segré, G. & Silberberg, A. 1962b Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 2. Experimental results and interpretation. J. Fluid Mech. 14, 136–157.Google Scholar
Shao, X., Yu, Z. & Sun, B. 2008 Inertial migration of spherical particles in circular Poiseuille flow at moderately high Reynolds numbers. Phys. Fluids 20, 103307.Google Scholar
Sollier, E., Go, D. E., Che, J., Gossett, D. R., Bryne, S. O., Weaver, W. M., Kummer, N., Retting, M., Goldman, J., Nickols, N., Mccloskey, S., Kulkarni, R. & Di Carlo, D. 2013 Size-selective collection of circulating tumor cells using vortex technology. Lab on a Chip 14, 63–77.CrossRefGoogle ScholarPubMed
Subramanian, G. & Koch, D. L. 2006 Inertial effects on the transfer of heat or mass from neutrally buoyant spheres in a steady linear velocity field. Phys. Fluids 18, 073302.Google Scholar
Taneda, S. 1956a Experimental investigation of the wake behind a sphere at low Reynolds numbers. J. Phys. Soc. Japan 11, 1104–1108.Google Scholar
Taneda, S. 1956b Experimental investigation of the wakes behind cylinders and plates at low Reynolds numbers. J. Phys. Soc. Japan 11, 302–307.Google Scholar
Tang, L., Wen, F., Yang, Y., Crowe, C. T. & Troutt, T. R. 1992 Self-organizing particle dispersion mechanism in a plane wake. Phys. Fluids 4, 2244–2251.CrossRefGoogle Scholar
Yang, Y., Crowe, C. T., Chung, J. N. & Troutt, T. R. 2000 Experiments on particle dispersion in a plane wake. Intl J. Multiphase Flow 26, 1583–1607.Google Scholar
Yeo, K. & Maxey, M. R. 2013 Dynamics and rheology of concentrated, finite-Reynolds-number suspensions in a homogeneous shear flow. Phys. Fluids 25, 053303.CrossRefGoogle Scholar
Zovatto, L. & Pedrizzetti, G. 2001 Flow about a circular cylinder between parallel walls. J. Fluid Mech. 440, 1–25.Google Scholar

Haddadi et al. supplementary movie

A single particle released in the free stream does not enter the wake region (δ = 0.09, Re = 18).

Download Haddadi et al. supplementary movie(Video)
Video 284.9 KB
Supplementary material: PDF

Haddadi et al. supplementary material

Supplementary material

Download Haddadi et al. supplementary material(PDF)
PDF 1.7 MB

Haddadi et al. supplementary movie

A single particle released in the wake region migrates outward and reaches a limit cycle trajectory. (δ = 0.09, Re = 18).

Download Haddadi et al. supplementary movie(Video)
Video 10.8 MB

Haddadi et al. supplementary movie

In addition to particle pairs, limit cycle is a stable trajectory for particle pairs (δ = 0.09, Re = 18).

Download Haddadi et al. supplementary movie(Video)
Video 8.2 MB

Haddadi et al. supplementary movie

Interaction between particles breaks the stability of the limit cycle and a particle exchange forms between the wake and free stream (δ = 0.09, Re = 18).

Download Haddadi et al. supplementary movie(Video)
Video 14.8 MB