Published online by Cambridge University Press: 23 January 2019
A linear stability analysis of a two-layer plane Couette flow of two immiscible fluid layers with different densities, viscosities and thicknesses, bounded by two infinite parallel plates moving at a constant relative velocity to each other, with an insoluble surfactant monolayer along the interface and in the presence of gravity is carried out. The normal modes approach is applied to the equations governing flow disturbances in the two layers. These equations, together with boundary conditions at the plates and the interface, yield a linear eigenvalue problem. When inertia is neglected the velocity amplitudes are the linear combinations of certain hyperbolic functions, and a quadratic dispersion equation for the increment, that is the complex growth rate, is obtained, where coefficients depend on the aspect ratio, the viscosity ratio, the basic velocity shear, the Marangoni number 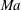 $Ma$ that measures the effects of surfactant and the Bond number
$Ma$ that measures the effects of surfactant and the Bond number 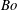 $Bo$ that measures the influence of gravity. An extensive investigation is carried out that examines the stabilizing or destabilizing influences of these parameters. Since the dispersion equation is quadratic in the growth rate, there are two continuous branches of the normal modes: a robust branch that exists even with no surfactant, and a surfactant branch that, to the contrary, vanishes when
$Bo$ that measures the influence of gravity. An extensive investigation is carried out that examines the stabilizing or destabilizing influences of these parameters. Since the dispersion equation is quadratic in the growth rate, there are two continuous branches of the normal modes: a robust branch that exists even with no surfactant, and a surfactant branch that, to the contrary, vanishes when 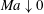 $Ma\downarrow 0$. Regimes have been uncovered with crossings of the two dispersion curves, their reconnections at the point of crossing and separations as
$Ma\downarrow 0$. Regimes have been uncovered with crossings of the two dispersion curves, their reconnections at the point of crossing and separations as 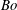 $Bo$ changes. Due to the availability of the explicit forms for the growth rates, in many instances the numerical results are corroborated with analytical asymptotics.
$Bo$ changes. Due to the availability of the explicit forms for the growth rates, in many instances the numerical results are corroborated with analytical asymptotics.